Tunneloituminen

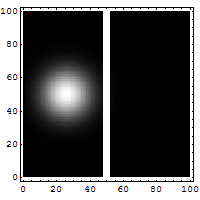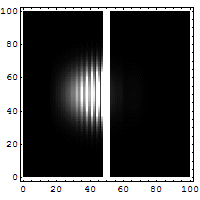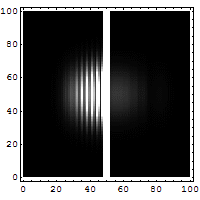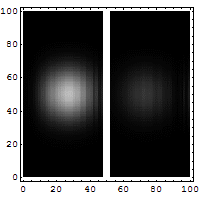
Tunneloituminen on ilmiö, jossa hiukkanen voi siirtyä läpi alueen, jolla liikkuminen ei klassisen mekaniikan mukaan olisi mahdollista. Tunneloitumisilmiö perustuu olettamukseen, että hiukkasella ei ole täsmällistä paikkaa, vaan sijainti esitetään todennäköisyysjakaumana. Jos klassisessa mielessä kielletyn alueen leveys on pieni, Schrödingerin yhtälön ratkaisuna tuleva todennäköisyysjakauma jatkuu sen toisella puolella. Oheisessa simulaatiossa elektroni törmää ohueen seinämään, josta sen ei klassisen fysiikan mukaan pitäisi päästä läpi. Elektronin sijainnin todennäköisyysjakauma on esitetty kirkkausvaihteluna: mitä kirkkaampi kohta, sitä todennäköisemmin siinä on elektroni. Himmeä pallo kulkee seinästä läpi ja kirkas heijastuu, eli elektroni tunneloituu pienellä todennäköisyydellä seinän läpi.

Arkipäiväinen tunneloitumista hyödyntävä sovellus ovat flash-muistit (muistitikut, SSD-levyt, ...). Niissä elektroneja voidaan varastoida eristekalvojen taakse kiihdyttämällä elektroneja jännitteen luomalla sähkökentällä kalvoa kohti. Riittävällä jännitteellä kiihdytetyt elektronit tunneloituvat eristekalvon taakse ja pysyvät siellä myös kytkettäessä kenttä pois päältä. Luettaessa muistia yksittäinen elektronisäiliö on nolla tai ykkönen sen mukaan, onko siellä elektroneja vai ei. Tunneloitumista hyödynnetään myös alle nanometrien luokkaa olevien rakenteiden kuvantamisessa. Laite on tunnelointimikroskooppi.

Video: Tunnelointimikroskoopin toimintaperiaate (La Physique Autrement)

Lomittuminen

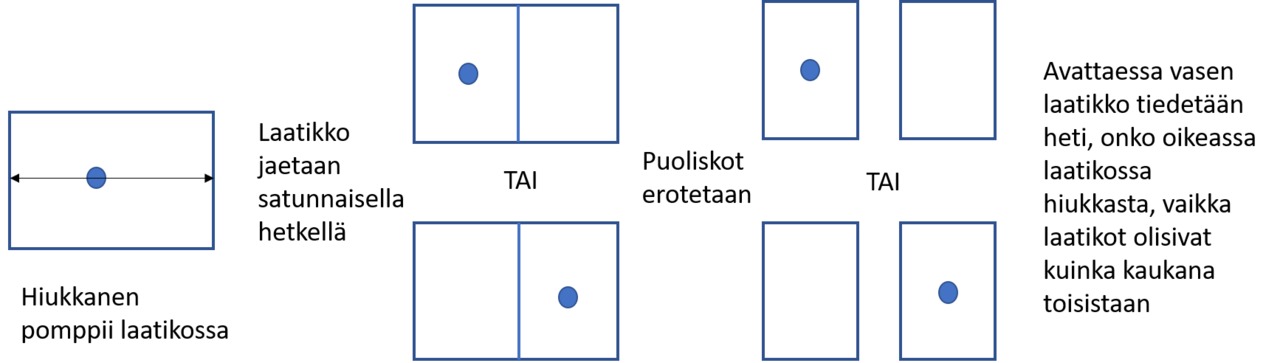
Lomittuminen on kvantti-ilmiö, jossa kaksi systeemiä ovat kytkeytyneet toisiinsa, eikä kummankaan tilaa voi kuvailla toisesta riippumattomalla tavalla. Kun yhden lomittuneen systeemin tilaa tutkitaan, toisen tila muuttuu välittömästi. Tarkastellaan esimerkkinä tilannetta, jossa hiukkanen pomppii edestakaisin laatikossa. Laatikko jaetaan satunnaisella hetkellä kahteen osaan. Hiukkanen jää oikealle tai vasemmalle puoliskolle. Jos puoliskot nyt erotetaan, ne ovat lomittuneet. Alkutilanteessa kummassakin puoliskossa on hiukkanen ja ei ole hiukkasta. Jos nyt oikeaa puoliskoa tutkitaan ja havaitaan hiukkasen olevan siellä, vasemman puoliskon tila on myös tiedossa: on selvää, että siellä ei ole hiukkasta. Vasemman puoliskon tila ei ollut riippumaton oikeasta. Vasemman puoliskon tila muuttuu välittömästi, kun oikean puoliskon tilaa tutkitaan. Tämä tapahtuu riippumatta siitä, kuinka kaukana puoliskot ovat toisistaan.

Tyypillinen lomittunut systeemi on kaksi alkeishiukkasta, esim. elektronipari, tai kaksi fotonia. Lomittuminen purkautuu mitattaessa jommankumman lomittuneen hiukkasen tila. Siksi lomittuminen rikkoutuu helposti vuorovaikutusten takia. Muiden kvantti-ilmiöiden tapaan lomittumista on siten hankala havaita makroskooppisilla hiukkasilla, koska niitä on vaikea täysin eristää vuorovaikutukselta ympäristön kanssa. Aalto-yliopistossa on kuitenkin onnistuttu todentamaan v. 2018 myös lähes makroskooppisten hiukkasten lomittuminen.

Einsteinin ennustama haamuvuorovaikutus (Aalto-yliopisto)

Yksi lomittumisen hyötykäyttö on herkkien kohteiden kuvaaminen. Kuvattavaan kohteeseen lähetetään matalaenergiaisia fotoneja, jotka ovat lomittuneet kameralle menevien korkeaenergiaisten fotonien kanssa. Kuva tulee tällöin otettua heti fotonien osuessa kohteeseen, ei vasta kohteesta sironneiden fotonien saapuessa takaisin kameraan. Lisäksi lomittuminen voidaan toteuttaa niin, että kameraan saapuvat fotonit ovat korkeaenergiaisia ja tulevat helposti havaittua kennolla, kun taas kuvattavaan näytteeseen osuvat fotonit ovat matalaenergiaisia, eivätkä vaurioita sitä. Tekniikka on hiljalleen leviämässä laajempaan käyttöön esim. valoherkkien biologisten näytteiden kuvaamisessa.

Lomittuneilla fotoneilla valokuvaaminen (Nature.com)

Lukuisat sovellukset pohjaavat kvantti-ilmiöihin. Jo lähitulevaisuudessa yksi merkittävä sovellus voi olla *kvanttitietokone.