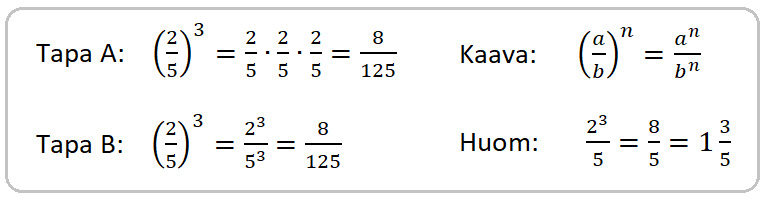7-8 Potenssi

Potenssin käsite

Johdanto

  • On ilmiöitä, joissa tietty lukumäärä kertautuu säännöllisellä ja toistuvalla tavalla.
  • Lasketaan peräkkäisin kertolaskuin
  • Potenssimerkintä tiivistää lausekkeen, jossa luku kerrotaan itsellään.
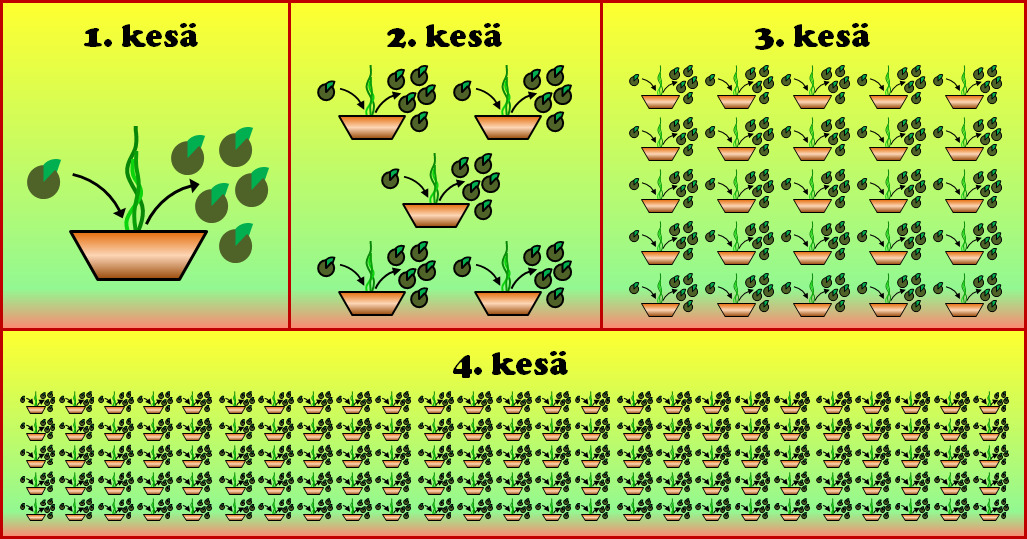
  • Ⓔ Sipulikasvin lisääntyminen
    • Viljelyskasvi versoo talvehtivasta sipulista.
    • Kasvi tuottaa kesän aikana viisi uutta sipulia
    • Talvehtineet sipulit istutetaan aina keväällä uudestaan
    • Kuinka paljon sipuleita maasta nousee neljännen kesän lopussa?



Laskeminen kertolaskun avulla:
5 ⋅ 5 ⋅ 5 ⋅ 5 = 625

  • Vastaus: Sipuleita nousee 4. kesän lopussa 625 kappaletta.
  • Ehkä tästä lähtien osan sipuleista voisi jo syödä tai myydä pois.

Laskeminen potenssilaskun avulla:
54 = 625

  • Sama tulos niin kuin pitikin!
  • Funktiolaskimella painetaan järjestyksessä näitä neljää näppäintä 5 yx 4 =

Videoesimerkki, kun yhdestä nuudelista tehdään 128
1 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 27 = 128
This Chef Can Make 128 Noodles in 10 Seconds

Potenssimerkintä

Potenssimerkintä

  • Muodostuu kantaluvusta ja exponentista
  • Kantalukua kerrotaan itsellään niin monta kertaa kuin exponentti määrää
  • Kaava: an = a ⋅ a ⋅ a ⋅ ... ⋅ a (tulontekijöinä n kappaletta a)
  • Missä a on kantaluku ja n on exponentti.
    Ⓔ Merkitse ja laske potenssilauseke, jossa kantaluku on 5 ja exponentti on 3.
    Merkitse: 53
    Laske: = 5 ⋅ 5 ⋅ 5 = 125

Luvun neliö

  • On luvun toinen potenssi eli exponentti on kaksi
  • Viittaa neliön pinta-alan laskukaavaan A=a2
  • Viittaa samalla siihen, että pinta-alan käsite vaatii kaksi ulottuvuutta, x ja y.
    Ⓔ Laske luvun kuusi neliö eli korota luku kuusi toiseen potenssiin
    Vastaus: 62 = 6 ⋅ 6 = 36

Luvun kuutio

  • On luvun kolmas potenssi eli exponentti on kolme
  • Viittaa kuution tilavuuden laskukaavaan V=a3
  • Viittaa samalla siihen, että tilavuuden hahmottaminen vaatii kolme ulottuvuutta, x, y ja z.
    Ⓔ Laske luvun kuusi kuutio eli korota luku kuusi kolmanteen potenssiin
    Vastaus: 63 = 6 ⋅ 6 ⋅ 6 = 216

Negatiivinen kantaluku

  • Vaatii sulkeet ympärilleen
  • Muuten etumerkki ei ole osa potenssilauseketta
  • Tulon merkkisääntöjen mukaan parillisilla exponenteilla potenssin arvo on positiivinen ja parittomilla negatiivinen.

Kantaluku 3 Potenssin arvo   Kantaluku −3 Potenssin arvo
31 = 3   (−3)1 = −3
32 = 3 ⋅ 3 = 9   (−3)2 = −3 ⋅ (−3) = 9
33 = 3 ⋅ 3 ⋅ 3 = 27   (−3)3 = −3 ⋅ (−3) ⋅ (−3) = −27
34 = 3 ⋅ 3 ⋅ 3 ⋅ 3 = 81   (−3)4 = −3 ⋅ (−3) ⋅ (−3) ⋅ (−3) = 81

Huom: −32 = − 3 ⋅ 3 = −9

Kantalukuna murtoluku

  • Vaatii sulkeet ympärilleen
  • Muuten exponentti vaikuttaa vain osoittajaan tai nimittäjään
    Ⓔ Laske potenssi, kun kantaluku on 2/5 ja eksponentti on 3

  • Huomaathan, että jakolasku voidaan aina tulkita murtolukuna.
    Ⓔ Siksi (2 : 5)3 = 23 : 53 = 8 : 125 = 8/125

Laskujärjestys

  1. Sulkeiden sisällä olevat laskutoimitukset (paitsi murtoluvut)
  2. Potenssimerkinnät
  3. Kerto- ja jakolaskut (vasemmalta oikealle)
  4. Yhteen- ja vähennyslaskut

Kymmenpotenssimuodot

Lämmittelyä

  • Osaat nyt laskujärjestyksen.
  • Sievennetään seuraava lauseke, jossa 5,7 km esitetään metreinä.
    5,7 km = 5,7 ⋅ 103 m = 5,7 ⋅ 10 ⋅ 10 ⋅ 10 m = 5 700 m
  • Liikuimme kolme askelta pituusyksiköissä, km → hm → dam → m
  • Siksi alkuperäinen luku kerrotaan kolmesti kymmenellä
  • Punaisella merkitty vaihe on luvun 5700 kymmenpotenssimuoto
  • Kymmenpotenssimuotoa tarvitaan erittäin suurten (monta numeroa) tai erittäin pienten (lähellä nollaa) olevien lukujen esittämiseen ja laskutoimituksiin.

Muodostaminen - suuret luvut

  • Kirjoita luvun merkitsevät numerot
  • Aseta pilkku ensimmäisen numeron oikealle puolelle
  • Lisää loppuun ⋅ 10n missä n on askelten määrä pilkun "oikealle paikalle"
  • Ⓔ Suomen asukasluku suunnilleen 2022
    5 560 000 = 5,56 ⋅ 106
    Voidaan lausua: 5,56 miljoonaa

Muodostaminen - pienet luvut

  • Muuten samoin kuin suuret luvut mutta eksponentissa on miinusmerkki
  • ⋅ 10−1 merkitsee kymmenkertaisen sijaan kymmenesosaa
  • Ⓔ Juomavedessä sallittu arseenipitoisuus
    kymmenen mikrogrammaa eli 0,000 010 grammaa litraa kohden
    0,000 010 g/l = 1,0 ⋅ 10−5 g/l
    Voidaan lausua: kymmenen gramman miljoonasosaa

Yhteenveto

1 ⋅ 103 = 1 ⋅ 1000 = 1000
1 ⋅ 102 = 1 ⋅ 100 = 100
1 ⋅ 101 = 1 ⋅ 10 = 10
1 ⋅ 100 = 1 ⋅ 1 = 1 Huom!
1 ⋅ 10−1 = 1 : 10 = 0,1
1 ⋅ 10−2 = 1 : 100 = 0,01
1 ⋅ 10−3 = 1 : 1000 = 0,001

Huom! Minkä tahansa luvun nollas potenssi on 1. Siksi 1 ⋅ 100 ei ole mielekäs merkintä.

Harjoittelua

Suomessa tuotetaan vuosittain 7,5 ⋅ 107 kg ruisviljaa. Yhteen rekkaan mahtuu noin 4,0 ⋅ 104 kg. Montako rekkaa tarvitaan?