4. Resistanssi
Resistanssi
Viime kappaleesssa puhuimme sähkövirrasta ja siitä, millaisia vaikutuksia sähkövirralla on. Esimerkiksi kun sähkövirta kulkee hehkulampun läpi, niin lampussa syntyy valoa ja lämpöä. Mutta mihin hehkulampun valoa ja lämpöä synnyttävä vaikutus perustuu?
Aineet jaetaan johteisiin ja eristeisiin niiden sähköä johtavan kykynsä perusteella. Johteet johtavat sähköä hyvin ja eristeet johtavat sähköä huonosti.
 Sähköjohdossa on kuparia, joka on johde, ja muovia, joka on eriste.
Sähköjohdossa on kuparia, joka on johde, ja muovia, joka on eriste.
Kaikki aineet vastustavat jonkin verran sähkövirran kulkua. Johtimen tai sähkölaitteen kykyä vastustaa sähkövirran kulkua kutsutaan resistanssiksi. Mitä isompi resistanssi johtimella tai laitteella on, niin sitä enemmän se vastustaa sähkövirran kulkua.
Resistanssin tunnus on [[$R$]] ja resistanssin yksikkö on ohmi [[$\Omega$]].
Johtimen resistanssin arvoon vaikuttaa kolme asiaa: johtimen materiaali, pituus ja paksuus. Mitä pidempi johdin on, niin sitä suurempi on sen resistanssi. Mitä ohuempi johdin on, niin sitä suurempi on sen resistanssi. Johtimen lämpötila vaikuttaa myös sen resistanssiin.
Alla olevalla sovelluksella voi kokeilla yllä mainittujen seikkojen vaikutusta resistanssin arvoon.
Esimerkiksi hehkulampun pitkä ja ohut hehkulanka (vastus) vastustaa sähkövirran kulkua. Suuren resistanssin takia hehkulampu kuumenee ja alkaa säteillä lämpöä ja valoa. Myös esimerkiksi sähkökiukaan vastusten lämpöä synnyttävä vaikutus johtuu resistanssista.
Sähkölaitteen resistanssi [[$R$]] voidaan laskea sähkölaitteen aiheuttaman jännitehäviön [[$U$]] ja sähkölaitteen läpi kulkevan virran [[$I$]] avulla kaavalla [[$$resistanssi= \frac{jännitehäviö}{sähkövirta}$$]] eli [[$$R=\frac{U}{I}.$$]]
Virtapiirissä on usein useita vastuksia kytkettynä sarjaan tai rinnan. Kytkentätyyppi vaikuttaa vastusten kokonaisresistanssiin.
Vastusten sarjaankytkentä
Kun vastuksia kytketään sarjaan, niin niiden kokonaisresistanssi saadaan laskemalla yksittäisten vastusten resistanssit yhteen.
 Kokonaisresistanssi [[$R$]] lasketaan laskemalla vastusten resistanssit yhteen eli [[$R=R_1 + R_2$]].
Kokonaisresistanssi [[$R$]] lasketaan laskemalla vastusten resistanssit yhteen eli [[$R=R_1 + R_2$]].
Vastusten rinnankytkentä
Kun vastuksia kytketään rinnan, niin niiden aiheuttama kokonaisresistanssi pienenee.
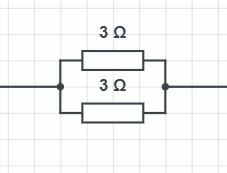
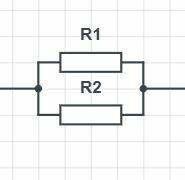 Rinnankytkettyjen vastusten [[$R_1$]] ja [[$R_2$]] aiheuttama kokonaisresistanssi [[$R$]] lasketaan kaavalla [[$\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2}$]].
Rinnankytkettyjen vastusten [[$R_1$]] ja [[$R_2$]] aiheuttama kokonaisresistanssi [[$R$]] lasketaan kaavalla [[$\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2}$]].
Resistanssi
Aineet jaetaan johteisiin ja eristeisiin niiden sähköä johtavan kykynsä perusteella. Johteet johtavat sähköä hyvin ja eristeet johtavat sähköä huonosti.
 Sähköjohdossa on kuparia, joka on johde, ja muovia, joka on eriste.
Sähköjohdossa on kuparia, joka on johde, ja muovia, joka on eriste.Kaikki aineet vastustavat jonkin verran sähkövirran kulkua. Johtimen tai sähkölaitteen kykyä vastustaa sähkövirran kulkua kutsutaan resistanssiksi. Mitä isompi resistanssi johtimella tai laitteella on, niin sitä enemmän se vastustaa sähkövirran kulkua.
Resistanssin tunnus on [[$R$]] ja resistanssin yksikkö on ohmi [[$\Omega$]].
Johtimen resistanssin arvoon vaikuttaa kolme asiaa: johtimen materiaali, pituus ja paksuus. Mitä pidempi johdin on, niin sitä suurempi on sen resistanssi. Mitä ohuempi johdin on, niin sitä suurempi on sen resistanssi. Johtimen lämpötila vaikuttaa myös sen resistanssiin.
Alla olevalla sovelluksella voi kokeilla yllä mainittujen seikkojen vaikutusta resistanssin arvoon.
Esimerkiksi hehkulampun pitkä ja ohut hehkulanka (vastus) vastustaa sähkövirran kulkua. Suuren resistanssin takia hehkulampu kuumenee ja alkaa säteillä lämpöä ja valoa. Myös esimerkiksi sähkökiukaan vastusten lämpöä synnyttävä vaikutus johtuu resistanssista.
Resistanssin laskeminen
Sähkölaitteen resistanssi [[$R$]] voidaan laskea sähkölaitteen aiheuttaman jännitehäviön [[$U$]] ja sähkölaitteen läpi kulkevan virran [[$I$]] avulla kaavalla [[$$resistanssi= \frac{jännitehäviö}{sähkövirta}$$]] eli [[$$R=\frac{U}{I}.$$]]
| Esimerkki. Hehkulamppu aiheuttaa [[$4,5 \ V$]] jännitehäviön, kun sen läpi kulkee [[$0,4 \ A$]] sähkövirta. Tällöin lampun resistanssi [[$R$]] on [[$$R = \frac{U}{I}=\frac{4,5 \ V}{0,4 \ A}=11,25 \ \Omega.$$]] |
Vastusten kytkentöjä
Virtapiirissä on usein useita vastuksia kytkettynä sarjaan tai rinnan. Kytkentätyyppi vaikuttaa vastusten kokonaisresistanssiin.
Vastusten sarjaankytkentä
Kun vastuksia kytketään sarjaan, niin niiden kokonaisresistanssi saadaan laskemalla yksittäisten vastusten resistanssit yhteen.
 Kokonaisresistanssi [[$R$]] lasketaan laskemalla vastusten resistanssit yhteen eli [[$R=R_1 + R_2$]].
Kokonaisresistanssi [[$R$]] lasketaan laskemalla vastusten resistanssit yhteen eli [[$R=R_1 + R_2$]].Esimerkki.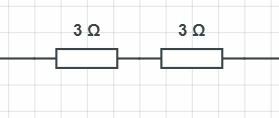 Kaksi [[$3 \ \Omega$]] vastusta on kytketty sarjaan. Tällöin niiden kokonaisresistanssi [[$R$]] on [[$$R \ = \ R_1 + R_2 \ = \ 3 \ \Omega + 3\ \Omega \ = \ 6 \ \Omega.$$]] |
Vastusten rinnankytkentä
Kun vastuksia kytketään rinnan, niin niiden aiheuttama kokonaisresistanssi pienenee.
 Rinnankytkettyjen vastusten [[$R_1$]] ja [[$R_2$]] aiheuttama kokonaisresistanssi [[$R$]] lasketaan kaavalla [[$\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2}$]].
Rinnankytkettyjen vastusten [[$R_1$]] ja [[$R_2$]] aiheuttama kokonaisresistanssi [[$R$]] lasketaan kaavalla [[$\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2}$]].