5.2 Kaasun tekemä työ ja lämpövoimakone

Kaasun tilavuuden muutostyö

Luvussa Kaasun tila ja tilanmuutokset käsiteltiin kaasun tilanmuutosta vakiolämpötilassa. Luvun tilanteessa kaasusäiliön tilavuutta pienennettiin hitaasti, jolloin tilavuus ja paine muuttuivat kääntäen verrannollisesti. Koska kokoonpuristaminen tehtiin hitaasti, kaasun lämpötila pysyi vakiona. Nopea tilavuuden muutos aiheuttaa toisentyyppisen tilanmuutoksen, kuten videolla havaitaan.

Nopeasti kokoonpuristetun kaasun lämpötila kasvaa niin paljon, että sylinterin pohjalla oleva paperinpala palaa leimahtaen. Kaasun lämpötila ei ehdi tasaantua ympäristön kanssa, vaan voi ylittää syttymiseen vaadittavan lämpötilan 200 celsiusastetta. Tämä johtuu sylinterin mäntää puristavan voiman tekemästä työstä. Mikroskooppisella tasolla työ ilmenee siten, että liikkuvasta männästä kimpoilevien kaasumolekyylien liike-energia kasvaa. Tällöin kaasun sisäenergia ja sen myötä lämpötila kasvavat.

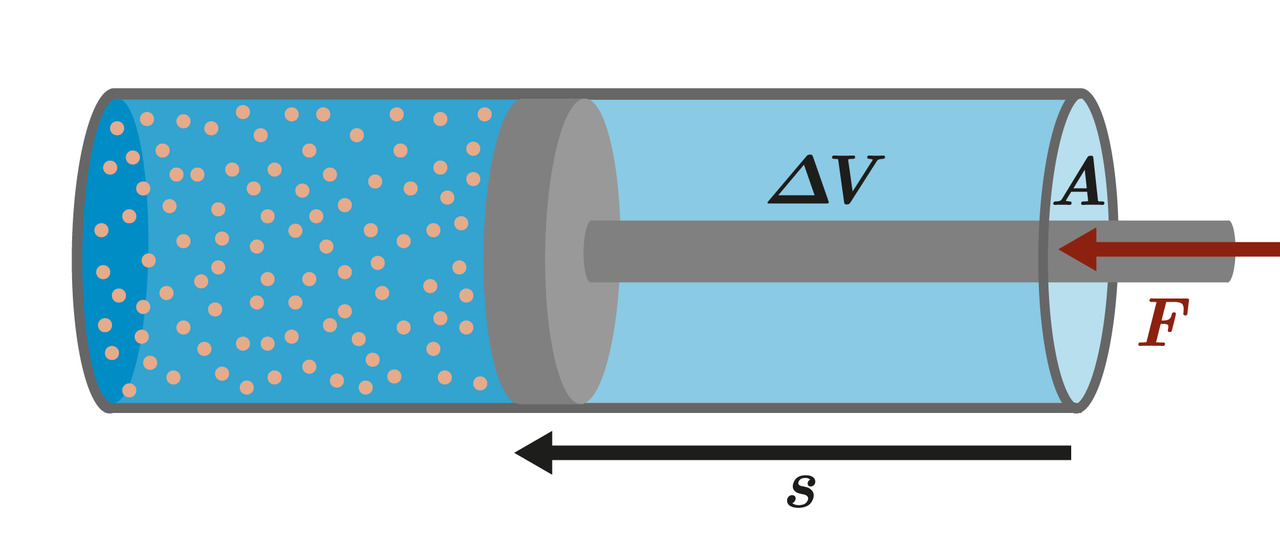
Kaasun puristamisessa tehtävän työn suuruudelle voidaan määrittää lauseke tilanteessa, jossa kaasun paine pysyy vakiona ja mäntää puristetaan voimalla F. Mäntä liikkuu kuvan mukaisesti voiman suuntaan matkan s. Työn suuruus lasketaan voiman ja matkan tulona, jolloin saadaan

[[$ \qquad W=Fs=pAs=p\Delta V $]], jossa [[$\Delta V$]] on kaasun tilavuuden muutos.

On syytä huomata, että leimahtavan paperinpalan tapauksessa kaasun paine ei pysy vakiona, vaan paine kasvaa. Tällaisessa tilanteessa työtä ei voida laskea paineen ja tilavuuden tulona.

Kun kaasua puristettiin kokoon, tehtiin työtä sen sisäenergian kasvattamiseksi. Prosessi voi tapahtua myös päinvastaiseen suuntaan. Laajeneva kaasu tekee työtä ympäristöön ja sen sisäenergia vähenee tehdyn työn verran. Esimerkkinä tällaisesta muutoksesta on autonrenkaan avatusta venttiilistä purkautuva ilma. Venttiilin havaitaan jäähtyvän, kun ilma jäähtyy virratessaan matalampaan paineeseen.

Työ kaasun tilavuuden muuttuessa

Puristettaessa kaasua kokoon vakiopaineessa tehdään työ [[$W$]], jonka suuruus on

[[$ \qquad W=p \Delta V $]],

missä [[$p$]] on kaasun paine ja [[$\Delta V$]] kaasun tilavuuden muutos. Kaasun sisäenergia kasvaa tehdyn työn verran.

Kaasun tilavuuden kasvaessa kaasu tekee samansuuruisen työn ympäristöön. Tällöin kaasun sisäenergia vähenee.

Termodynamiikan 1. pääsääntö kaasua puristettaessa

Edellä on tarkasteltu kaasua puristettaessa tehtävää työtä. Nopea ja hidas puristaminen eroavat toisistaan lämmön tavassa siirtyä kaasusta ympäristöön. Hitaasti tapahtuvassa isotermisessä tilavuuden muutoksessa kaasun lämpötila ei muutu, mikä tarkoittaa, että myöskään kaasun sisäenergia ei muutu. Kaasusta siirtyy siis tehdyn työn verran lämpöä ympäristöön. Nopeassa tilavuuden muutoksessa näin ei tapahdu, vaan osa tehdystä työstä muuttuu kaasun sisäenergiaksi ja nostaa kaasun lämpötilaa. Erikoistapaus on adiabaattinen tilanmuutos, jossa lämpöä ei siirry lainkaan systeemistä ympäristöön.

Termodynamiikan ensimmäisen pääsäännön mukaan systeemin sisäenergia [[$\Delta U$]] voi muuttua joko systeemiin tehdyn mekaanisen työn [[$W$]] tai systeemiin siirtyvän lämmön [[$Q$]] kautta.

[[$\quad \Delta U=Q+W$]]

Taulukossa vertaillaan isotermistä ja adiabaattista tilanmuutosta lämpöopin 1. pääsäännön näkökulmasta.

Kaasun puristaminen ja termodynamiikan 1. pääsääntö
	Isoterminen puristaminen	Adiabaattinen puristaminen
Työ [[$W$]]	Puristava voima tekee kaasuun työtä [[$W>0$]]	Puristava voima tekee kaasuun työtä [[$W>0$]]
Lämpö [[$Q$]]	Kaasusta siirtyy lämpöä ympäristöön [[$Q<0$]]	Lämpöä ei siirry [[$Q=0$]]
Kaasun sisäenergian muutos [[$\Delta U$]]	Kaasun lämpötila ei muutu, eikä sisäenergia [[$\Delta U=0$]], joten [[$W+Q=0$]]	Kaasun lämpötila nousee ja sisäenergia kasvaa: [[$\Delta U>0$]]

Kaasuprosessit tilavuus–paine-koordinaatistossa

Isotermisessä tilanmuutoksessa lämpötila on vakio, joten paine ja tilavuus muuttuvat kääntäen verrannollisesti toisiinsa nähden. Kääntäen verrannollisuutta ilmaiseva matemaattinen malli on muotoa

[[$ \qquad pV=\text{vakio} \quad $]] eli [[$ \quad p=\dfrac{\text{vakio}}{V} $]].

Tilavuus–paine-kuvaaja on hyberbeli. Yhtälössä esiintyvän vakion arvo riippuu lämpötilasta. Tämä ilmenee koordinaatistossa eri kohdissa kulkevina kuvaajina.

Sama esitystapa soveltuu myös muihin prosesseihin. Kaasun alkutilaa edustaa yksi piste tilavuus–paine-koordinaatistossa ja lopputilaa toinen. Alla olevassa kuvaajassa on esitetty isokoorinen ja isobaarinen prosessi.

Kuvaajan pystysuora osa esittää isokoorista muutosta, jossa tilavuus on vakio. Kaasun tekemä työ on nolla, koska tilavuus ei muutu. Paineen laskiessa arvosta p₁ arvoon p₂ täytyy lämpötilan laskea, sillä isokoorisessa muutoksessa pätee laki [[$ \frac {p}{T}=\text{vakio} $]]. Kaasu siis luovuttaa lämpöä ympäristöön ja sen sisäenergia vähenee. Esimerkki tällaisesta tapahtumasta on kylmään ympäristöön viety suljettu lasipullo. Prosessi tapahtuisi vastakkaiseen suuntaan pulloa lämmitettäessä.

Vaakasuorassa osassa paine pysyy vakiona ja tilavuus kasvaa arvosta V₁ arvoon V₂. Kyseessä on isobaarinen prosessi. Tilavuuden kasvaessa kaasu tekee ympäristöön työn [[$ W=p\Delta V=p(V_2-V_1) $]]. Koska isobaarisessa prosessissa pätee riippuvuus [[$ \frac {V}{T}=\text{vakio} $]], kaasun lämpötila kasvaa tilavuuden kasvaessa. Lämpötilan kasvu on seurausta lämmöstä, jota siirtyy ympäristöstä kaasuun. Tässä prosessissa siirtyvä lämpö siis saa aikaan sekä sisäenergian kasvua että työtä ympäristöön. Esimerkki tällaisesta tapahtumasta on laajeneva ilmapallo, joka siirretään varjosta auringonvaloon. Jos sama muutos tapahtuisi vastakkaiseen suuntaan, kyseessä olisi jäähtyvä kaasu, jonka tilavuus pienenee.

Isokoorinen ja isobaarinen tilanmuutos
	Isokoorinen muutos	Isobaarinen muutos
Tilanyhtälön suureet	Tilavuus [[$V$]] vakio. Paine ja lämpötila suoraan verrannolliset: [[$\dfrac{p}{T}=\text{vakio}$]].	Paine [[$p$]] vakio. Tilavuus ja lämpötila suoraan verrannolliset: [[$\dfrac{V}{T}=\text{vakio}$]].
Työ [[$W$]]	Työtä ei tehdä, koska tilavuus ei muutu. [[$W=0$]]	Tilavuuden muutostyö kaasuun tai ympäristöön. [[$W=\pm p\Delta V$]]
Lämpö [[$Q$]]	Lämpöä siirtyy lämpötilan muuttuessa. Lämmön etumerkki on sama kuin lämpötilan muutoksen.	Lämpöä siirtyy lämpötilan muuttuessa. Lämmön etumerkki on sama kuin lämpötilan muutoksen.
Kaasun sisäenergian muutos [[$\Delta U$]]	Sisäenergia kasvaa lämpötilan kasvaessa ja vähenee lämpötilan laskiessa.	Sisäenergia kasvaa lämpötilan kasvaessa ja vähenee lämpötilan laskiessa.

Lämpövoimakone

Mekaanisen työn muuntuminen lämmöksi on tavallinen ilmiö paitsi luonnossa myös laitteiden toiminnassa. Laitteet lämpenevät, kun niitä käytetään. Lämpövoimakone on laite, joka muuntaa energiaa päinvastaiseen suuntaan. Lämpövoimakoneessa lämmöstä tuotetaan mekaanista energiaa.

Useimmissa lämpövoimakoneissa hyödynnetään laajenevan kaasun tekemää työtä. Kaasua lämmitetään, se laajenee ja tekee työtä. Samalla kaasun sisäenergia muuntuu mekaaniseksi energiaksi, joka toteutuksesta riippuen työntää mäntää tai pyörittää turbiinia. Laajetessaan jäähtynyt kaasu ohjataan uudelleen lämmitettäväksi. Kaasun tilanmuutokset mahdollistavat kiertoprosessin, jossa kaasun sisäenergiaa muuntuu mekaaniseksi energiaksi niin kauan kuin kaasun lämmitystä jatketaan.

Ihminen on jo pitkään kyennyt vapauttamaan aineisiin sitoutunutta kemiallista energiaa polttamalla polttoaineita, mutta kemiallista energiaa opittiin muuntamaan mekaaniseksi työksi merkittävissä määrin vasta 1700-luvulla. Tällöin kehitettiin ensimmäiset höyrykoneet, jotka toimivat voimanlähteinä teollisuudessa ja hieman myöhemmin höyryvetureissa. Höyrykoneessa kuumennetaan polttoaineen avulla vettä, joka höyrystyessään nostaa systeemin painetta. Paineen kasvaessa höyry pyrkii laajenemaan. Laajeneva kaasu tekee työtä ympäristöön, mikä saa männän liikkeelle. Alla oleva animaatio esittää höyrykonetta, jossa höyry liikuttaa mäntää. Luistin avulla höyry ohjataan vuorotellen männän eri puolille, jolloin saadaan aikaan jatkuva edestakainen liike.

Lähde: Wikimedia

Lämpövoimakoneeksi nimitetään mitä tahansa laitetta, joka muuntaa kuuman aineen sisäenergiaa mekaaniseksi energiaksi. Nykyaikaisessa lämpövoimalaitoksessa poltetaan polttokattilassa polttoainetta, joka höyrystää vettä. Sisäenergiaa sitoutuu kuumaan höyryyn, joka siirtyy koneessa kohti turbiinia pyörittäen sitä. Pyörimisliike on mekaanista energiaa, joka muuntuu generaattorissa sähköksi. Jäljelle jäänyt höyry jäähtyy lauhduttimessa takaisin lämmitettäväksi. Alla on kaavakuva lämpövoimalaitoksesta sekä energiakaavio lämpövoimakoneesta.

Energiakaavio esittää lämpövoimakoneen toimintaa yleisellä tasolla. Lämpövoimalaitoksessa polttokattila on koneen lämpösäiliö ja lauhdutin kylmäsäiliö. Energia säilyy siten, että lämpösäiliöstä otettu lämpö [[$Q_1$]] on yhtä suuri kuin kylmäsäiliöön siirtyvä lämpö [[$Q_2$]] ja koneesta saatu mekaaninen työ [[$W$]].

[[$\qquad Q_1=Q_2+W$]]

Lämpövoimakoneen avulla halutaan tuottaa mahdollisimman paljon mekaanista työtä käytettävissä olevasta energiasta. Pyritään siis korkeaan hyötysuhteeseen. Lämpövoimakoneen hyötysuhde on mekaanisen työn osuus kaikesta lämpösäiliöstä otetusta energiasta.

[[$\qquad \eta= \dfrac{W}{Q_1}$]]

Todellista hyötysuhdetta määritettäessä on vielä tutkittava, kuinka paljon työstä saadaan muunnettua käyttötarkoituksen mukaiseen muotoon. Kaikkea työtä ei saada hyödynnettyä, koska osa mekaanisesta energiasta siirtyy ympäristöön lämpönä laitteen toimiessa.

Vaikka nykyaikaiset lämpövoimakoneet ovat muuttuneet 1700-luvun koneisiin verrattuna tehokkaammiksi ja hyötysuhteeltaan paremmiksi, termodynamiikan lait määräävät hyötysuhteelle teoreettisen ylärajan. Tavanomaisessa hiilivoimalassa tämä raja on suuruusluokaltaan 0,6 eli 60 %. Hyötysuhteen nostamiseksi lämpö- ja kylmäsäiliöiden välisen lämpötilaeron pitää olla mahdollisimman suuri ja kylmäsäiliön lämpötilan mahdollisimman pieni. 100 %:n hyötysuhde vaatisi kylmäsäiliön lämpötilaksi nolla kelviniä. Tämä tarkoittaa absoluuttista nollapistettä ja on mahdotonta. Tällainen kone olisi eräänlainen ikiliikkuja, joka muuttaisi kaiken säiliöstä ottamansa lämmön työksi. Tällä työllä voitaisiin jälleen lämmittää lämpösäiliötä, ja kone toimisi itsestään ikuisesti.

Jäähdytyskone

Jääkaapin toiminta perustuu pakotettuihin olomuodon muutoksiin. Korkeapaineinen jäähdytysneste johdetaan jääkaapin sisäiseen putkistoon venttiilistä, jossa sen paine laskee huomattavasti. Paineen aleneminen saa nesteen höyrystymään. Höyrystyminen vaatii energiaa, joten neste ja jääkaapin sisäosat jäähtyvät. Prosessi saadaan jatkuvaksi, kun höyry puristetaan kompressorissa uudelleen korkeapaineiseksi nesteeksi. Nesteytyminen vapauttaa energiaa lämpönä ympäristöön, minkä vuoksi kompressointi toteutetaan jääkaapin takaosassa, josta lämpö siirtyy huoneilmaan. Jääkaapin rakenne on esitetty alla olevassa kuvassa.

Jääkaappi on esimerkki jäähdytyskoneesta, jonka yleinen energiakaavio on esitetty kuvassa jääkaapin rinnalla. Jäähdytyskone on laite, joka siirtää lämpöä kylmäsäiliöstä kuumaan säiliöön. Jäähdytyskoneen toiminta on siis lämpövoimakoneeseen verrattuna vastakkainen. Lämpö ei siirry itsestään kylmästä kuumaan, vaan sen siirtämiseksi pitää tehdä työtä. Jääkaapin tapauksessa työtä tehdään, kun jäähdytysnesteen muodostamaa höyryä puristetaan korkeaan paineeseen. Jääkaapin kompressori tarvitsee tähän energiaa sähköverkosta. Jääkaapin lisäksi esimerkiksi ilmalämpöpumppu on jäähdytyskone. Vaikka sitä käytetään lämmittämiseen, lämpöopin näkökulmasta se toimii jäähdytyskoneen tavoin ja jäähdyttää ulkoilmaa lämmittäessään sisäilmaa.

Pysähdy pohtimaan

Esimerkit

Esimerkki 1

Suljettu kaasusysteemi käy läpi kuvaajan esittämät tilanmuutokset 1[[$\rightarrow$]]2 ja 2[[$\rightarrow$]]3.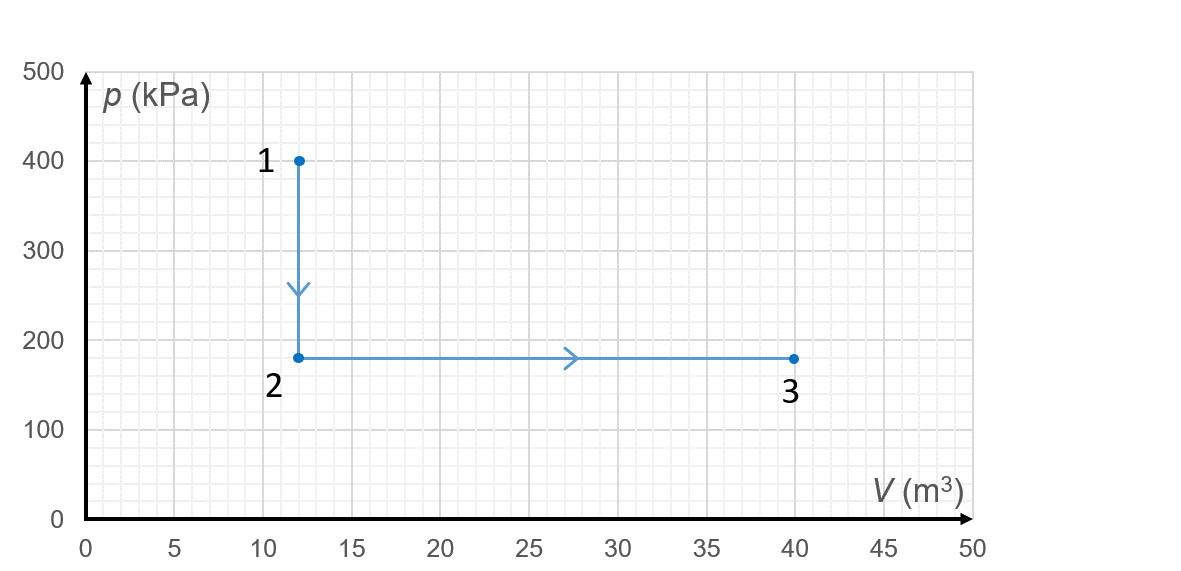

Määritä kaasun ja ympäristön välillä tehdyn työn suuruus molemmissa muutoksissa. Tehdäänkö kaasuun työtä vai tekeekö kaasu työtä ympäristöön?
Muutoksessa 1[[$\rightarrow$]]2 kaasun ja ympäristön välillä siirtyvän lämmön suuruus on 6 500 kJ ja muutoksessa 2[[$\rightarrow$]]3 se on 17 500 kJ. Laske kaasun sisäenergian muutos koko prosessissa.

Näytä ratkaisu

Esimerkki 2

Erästä turvevoimalaa käytetään talvisin sähköntarpeen ollessa huipussaan. Voimalassa poltetaan turvetta teholla 29 MW ja sen hyötysuhde sähköä tuottavana lämpövoimakoneena on 33 %.

Laske teho, jolla voimala tekee työtä ja teho, jolla voimalasta menee lämpöä kylmäsäiliöön.
Voimalan kokonaishyötysuhdetta voidaan kasvattaa, koska kylmäsäiliöön menevää lämpöä voidaan käyttää talvisin kaukolämpöverkossa. Kylmäsäiliöön menevästä lämmöstä saadaan hyödynnettyä tähän tarkoitukseen 85 %. Laske teho, jolla voimala tuottaa kaukolämpöä, ja voimalan kokonaishyötysuhde.

Näytä ratkaisu