Drawing a perpendicular bisector to a line segment

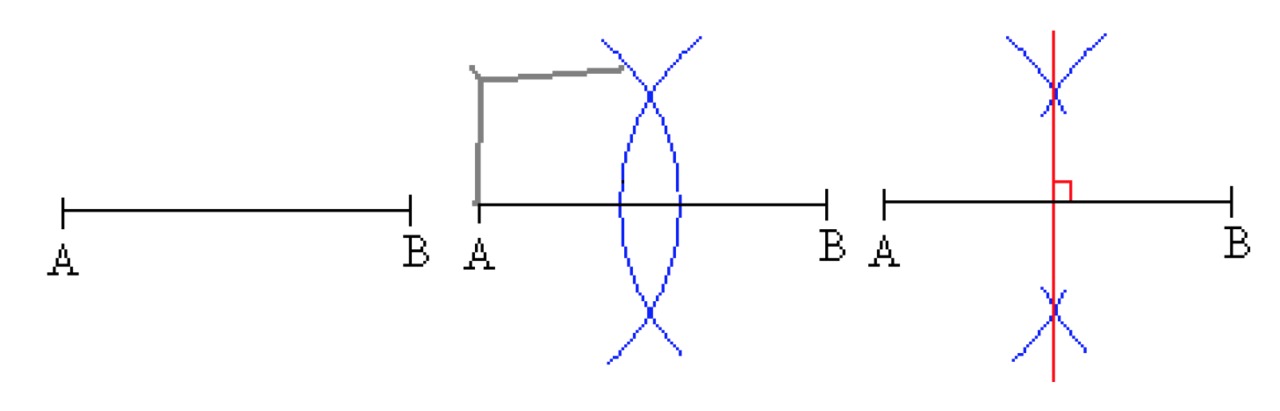
1. Draw the endpoints of the line segment [[$ A $]] and [[$ B $]] as the midpoints of two intersecting circular arcs of the same radius.
2. Draw a line passing through the intersections of the circular arcs. This line is the perpendicular bisector of the line segment [[$ AB $]].

Drawing a angle bisector

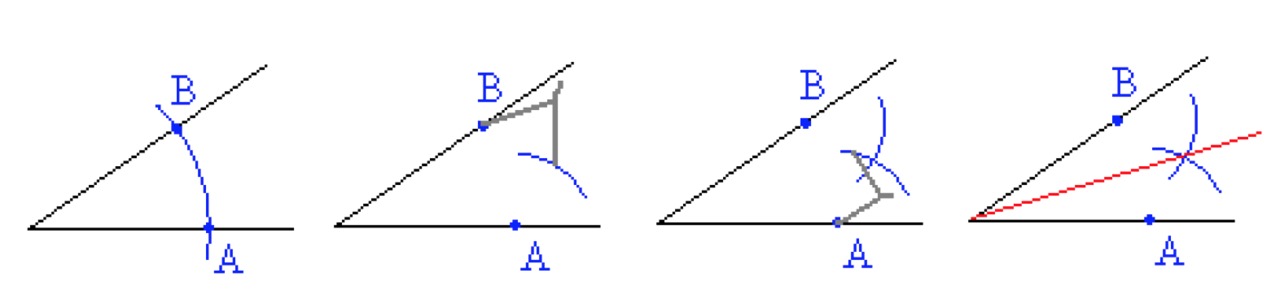
1. A circular arc is drawn with the corner of the angle as its center so that it intersects both of the angle's sides. 
2. The points of intersection [[$ A $]] and [[$ B $]] are drawn as the midpoints of circles with the same radius so that they intersect inside the angle.
3. The intersection of the two arcs is connected to the center of the angle. This ray forms the angle bisector. 

The altitude line, the median, the angle bisector, and the perpendicular bisector of a line are segments and lines associated with a triangle. They each have a surprising feature.

The altitudes of a triangle (or their extensions) intersect at the same point.

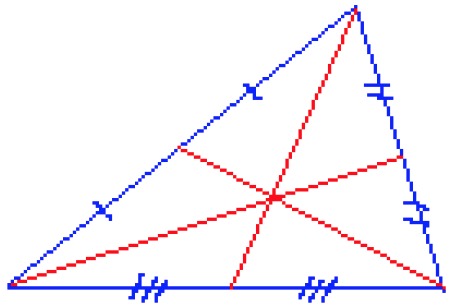
The segment drawn from the apex of the triangle to the center of its opposite side is called the median.The medians of a triangle intersect at the same point, which is called the triangle's centroid.

The bisectors of a triangle's angles intersect at the same point.





The perpendicular bisectors of a triangle's sides intersect at the same point.

It follows that a circle can be drawn inside each triangle so that it flanks each side of the triangle. The intersection point of the bisectors of the triangle's angles is the center of this circle.

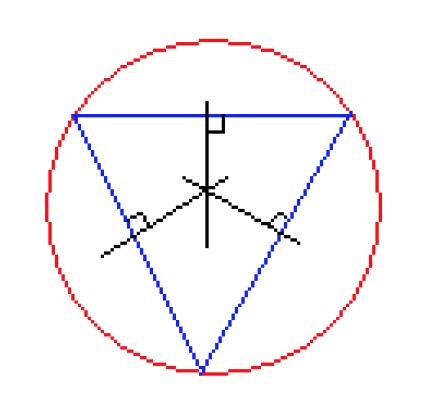
It also follows that a circle can be drawn around each triangle so that each of the triangle's vertices lie on the circle'scircumference. The triangle's centroid is the center of this circle.

Example 1

Three houses have a common yard. A common barbecue shelter will be built in the yard. Where should it be placed so that it is at an equal distance from each house? Draw a picture showing the location of the barbecue shelter when the distances between the houses are [[$ 48 $]] m, [[$ 60 $]] m, and [[$ 80 $]] m.

Solution:

In the drawing, mark the houses with the letters [[$ A $]], [[$ B $]] and [[$ C $]]. Let us first draw a line segment [[$ AB $]] with a length of is [[$ 80 $]] m. The location of the house [[$ C $]] is determined with a compass, using the points [[$ A $]] and [ [$ B $]] as midpoints of circular arcs with radius lengths of [[$ 60 $]] m and [[$ 48 $]] m.

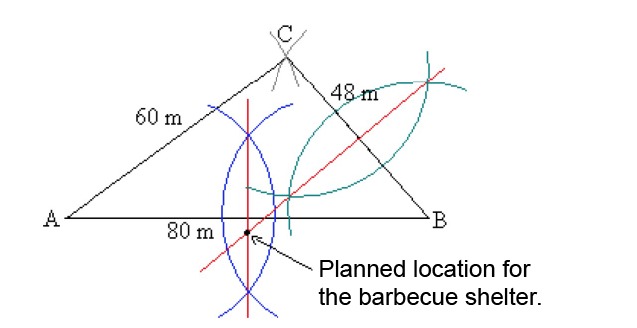
In order for the barbecue area to be equidistant from the houses [[$ A $]] and [[$ B $]], it must be at the perpendicular bisector of segment [[$ AB $]]. Similarly, in order for it to be equidistant from the houses [[$ B $]] and [[$ C $]], the barcbecue shelter must be located at the perpendicular bisector of the segment [[$ BC $]]. At the intersection of the perpendicular bisectors, you will find a place that is at an equal distance from all the houses.

Note! You can check the validity of your answer by drawing the perpendicular bisector for the segment [[$ AC $]]. For the answer to be correct, the perpendicular bisector of the segment [[$ AC $]] must intersect the perpendicular bisectors of the other sides at the same point.