Is the sum of the angles of the triangle really [[$ 180 ° $]]? We could draw a set of different triangles and measure the angles of each triangle separately and add them together. The sum of the angles of the triangle might be something between [[$ 178 $]] degrees and [[$ 182 $]] degrees. We could assume that the claim is quite true. In mathematics, such an action is not a proof but rather an approximate assessment of whether the assertion can even be true.

The statement must be proved to be true by any numerical value. In other words, a mathematical formula must be universally valid. In mathematics, important facts that are proven to be true with any numerical value are recorded as theorems. The certificates of the theorems are based on previous certificates based on basic information accepted without proof or axioms. A task where a theorem must be proven usually contains three parts: the assumption, the argument and the proof.

Example 1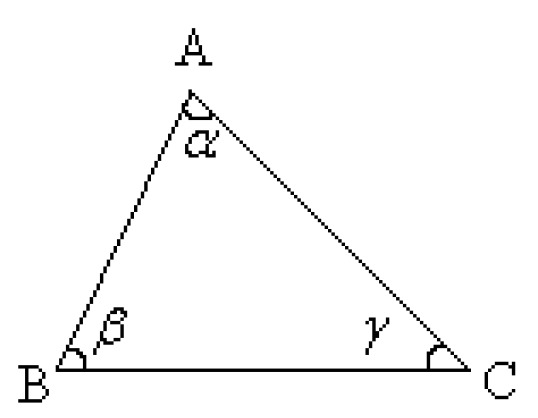

Prove that the sum of the angles of the triangle is [[$ 180° $]].​

Assumption: Triangle [[$ ABC $]]​ has angles of [[$ \alpha $]]​, [[$ \beta $]]​ and [[$ γ $]].​

Claim: The sum of the angles of a triangle is [[$ 180° $]].​

Proof:

First, draw the triangle [[$ ABC $]] and mark its angles with variables [[$ \alpha $]], [[$ \beta $]] and [[$ \gamma $]]. To be universal, specific numeric values cannot be selected for the angles.

The idea of the proof is to make use of previously known general information about angles. Draw a line that is parallel to the base side [[$ BC $]] and passes through point [[$ A $]]. Draw extensions to sides [[$ BA $]] and [[$ CA $]].

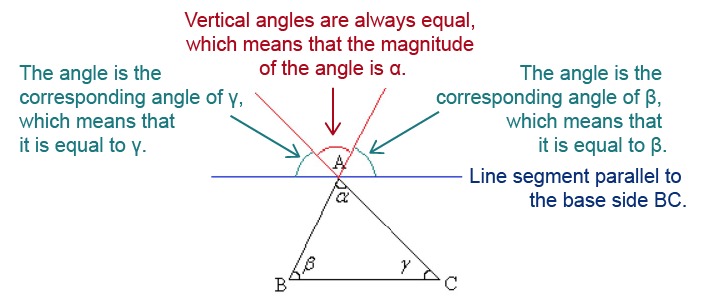
The angle formed by the angles [[$ \alpha $]], [[$ \beta $]] and [[$ \gamma $]] is a straight angle. This means that [[$ \alpha + \beta + \gamma = 180 ° $]]. This proves that the claim is true.

Example 2

Prove that the Pythagorean theorem is true.

Assumption: The lengths of the legs of a right triangle are [[$ a $]] and [[$ b $]] and the length of the hypotenuse is [[$ c $]].

Claim: [[$ a^2 + b^2 = c^2 $]]​

Proof:
The area of the larger square is

[[$ (a + b)(a + b) = a^2 + ab + ab + b^2 = a^2 + 2ab + b^2. $]]​

On the other hand, the area of the larger square is obtained by adding the area of the smaller square and the areas of the four triangles together.

[[$ c^2 + 4 \cdot \displaystyle\frac {ab} {2} = c^2 + 2ab $]]​

The expressions for the previous areas must be equal.

[[$ \begin{align*} a^2 + 2ab + b^2 &= c^2 + 2ab \\ a^2 + b^2 &= c^2 + 2ab - 2ab \\ a^2 + b^2 &= c^2  \end{align*} $]]​

This means that the claim is true.