5. Reflection with respect to an axis
Reflection with respect to an axis
If it is required to make a pattern that is similar to a original pattern, various similarity descriptions can be used. These similarity descriptions are reflection with respect to an axis, reflection with respect to a point, rotation and translation. By using the coordinate system, the figures and their simlarity descriptions can be presented computationally. Computer graphics are also based on these same principles.
Reflection with respect to an axis
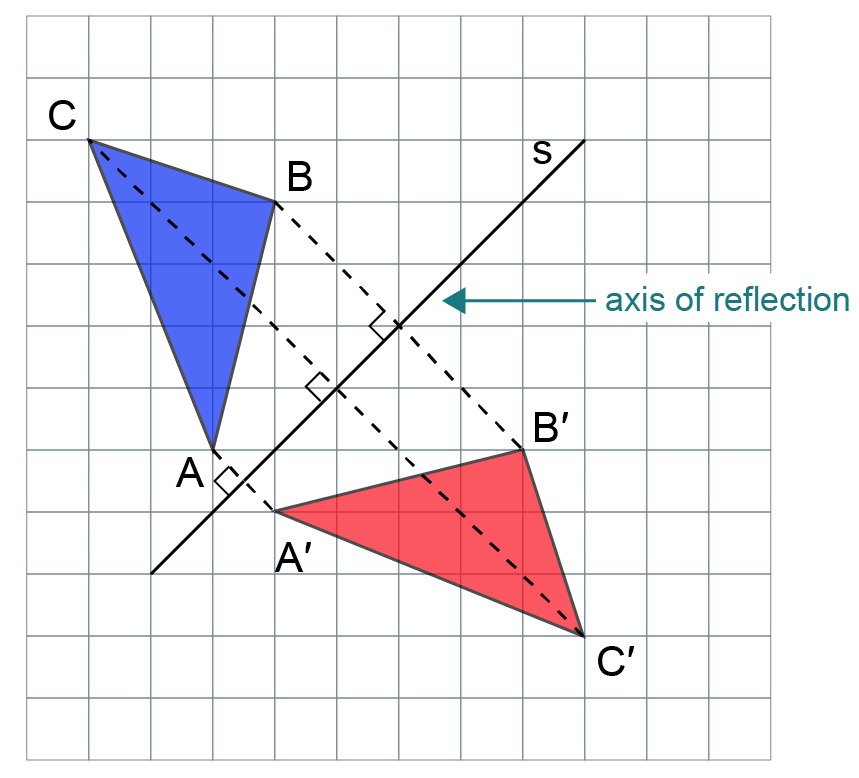
When reflecting a figure with respect to an axis, the corresponding points of the two figures are- on the same perpendicular of the axis.
- equally far from the axis.
If one of the similarity descriptions returns the pattern to exactly the same place it was originally, there will be symmetry in the pattern. A pattern that is reflected through an axis is said to be symmetrical about an axis. The axis is then called the axis of symmetry.
Example 1
Reflecting the triangle [[$ ABC $]] with respect to the line [[$ s $]] gives a reflected triangle [[$ A'B'C' $]], which is similar to the original triangle.
Example 2
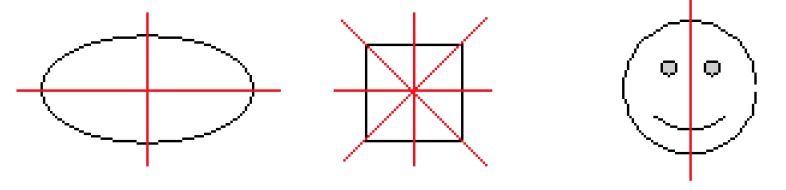
Below, you can see some examples of patterns that are symmetrical about an axis. The axes of reflection are marked in red.
Exercises
Basic exercises
Applied exercises
3/05. Submission folder for answers
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.