15. The inscribed and central angles of a circle
The inscribed and central angles of a circle
The inscribed angle of a circle is the angle whose vertex is on the circumference of the circle, and whose side consists of either two chords or a chord and a tangent. The part of the circumference between the sides of the inscribed angle is called the arc corresponding to the inscribed angle. In turn, the central angle corresponding to the inscribed angle is located at the center of the circle, and its sides separate the arc corresponding to the inscribed angle from the circle.
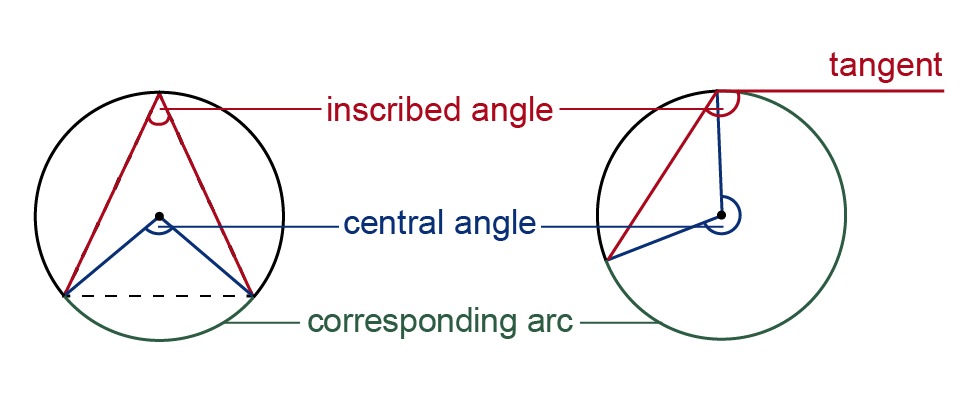
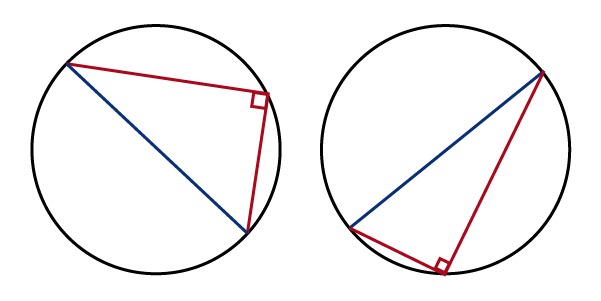
Thales' theorem:
Two line segments drawn from the endpoints of a circle's diameter to a point on the circle's circumference are always perpendicular to one another. As a result, the angle they create on the circle's arc is always a right angle.
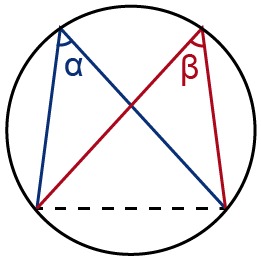
If the inscribed angle is drawn from a chord of a circle that is not the circle's diameter, the inscribed angle is not [[$ 90° $]]. However, inscribed angles that are drawn to the circumference from the same chord are always equal if they are located on the same segment of the circle.
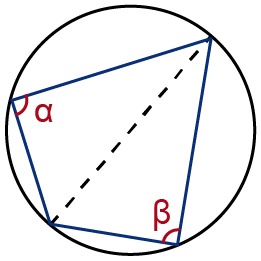
In other words, if two inscribed angles are located on the same side of the chord, their magnitudes are equal. Conversely, if two inscribed angles are drawn from the same chord so that they are located on different segments, the sum of the inscribed angles is [[$ 180° $]].
Inscribed angles that are located on the same segment of the circle and correspond to the same arc are always equal.
 |
 |
| Inscribed angles on the same segment α = β |
Inscribed angles on different segments α + β = 180° |
The inscribed angle theorem
The central angle is always twice as large as the corresponding inscribed angle, given that the two angles are connected to the same chord.

Example 1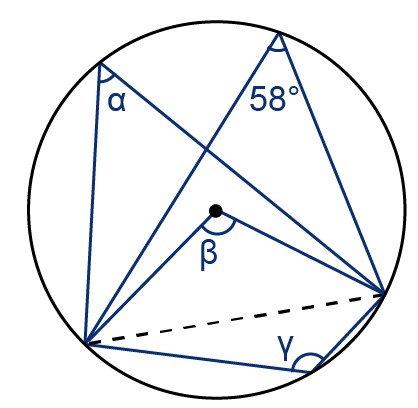
Determine the magnitudes of angles [[$ \alpha $]], [[$ \beta $]] and [[$ \gamma $]].
Since all the inscribed angles and the central angle are drawn from the same chord of the circle, the theorems introduced above can be applied.

Two inscribed angles located on the same segment are always equal, which means that [[$ \alpha = 58° $]].
The central angle is always twice as large as its corresponding inscribed angle, which means that [[$ \beta = 2 \cdot 58° = 116° $]].
The angle (gamma) is located on a different segment than angle 58, which means that [[$ \gamma + 58° = 180° $]] or [[$ \gamma = 180° -58° = 124° $]].
Answer: [[$ \alpha = 58° $]], [[$ \beta = 116° $]] and [[$ \gamma = 124° $]]
Exercises
Basic exercises
Applied exercises
Challenging exercises
3/15. Submission folder for answers
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.