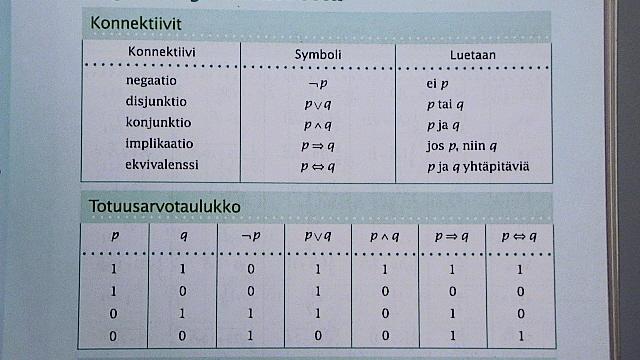
0. MAOLssa on tarvittavien konnektiivien totuustaulukot.
Käytä näitä hyväksesi muodostaaksesi monimutkaisempien lauseiden totuustalukot



1. Formalisoi lause.

Esim. Pitkä matematiikka 11 teht. 17c:
A = "Annu osaa ratkaista tehtävän" ja B = "Eino osaa ratkaista tehtävän".
Silloin lause C = "Annu osaa mutta Eino ei osaa" voidaan formalisoida muotoon [[$ A\wedge \neg B $]]. Missä tilanteissa lause C on tosi?

2. Listaa taulukkoon kaikki tarvittavien lauseiden totuusarvot.
Esimerkissä tarvitaan vain A ja B, joten taulukkoon tulee vain kaksi saraketta ja neljä riviä vastaten kaikkia A:n ja B:n eri kombinaatioita (joita on siis aina [[$ 2^n $]] kpl). Jos lausekkeita on enemmän kuin kaksi niin ole tarkkana että listaat kaikki eri kombinaatiot!

A	B
1	1
1	0
0	1
0	0

3. Etene kohti lopullisen lauseen totuustaulukkoa vaiheittain.
Laskujärjestys: sulkeet -> negaatio --> konjunktio ja disjunktio --> implikaatio ja ekvivalenssi. Esimerkissä siis ensin "negaatio B" ja sitten vasta "A:n ja ei-B:n konjunktio".

A	B	ei-B	A ja ei-B
1	1	0	0
1	0	1	1
0	1	0	0
0	0	1	0

4. Vasta kysymykseen (yleensä viimeisen sarakkeen perusteella).
Esimerkissä siis lause C on tosi rivillä kaksi eli kun A on tosi ja B epätosi eli kun "Annu osaa mutta Eino ei".