Aihe 1: Totuustaulukot

Koneektiivit ja totuustaulukot

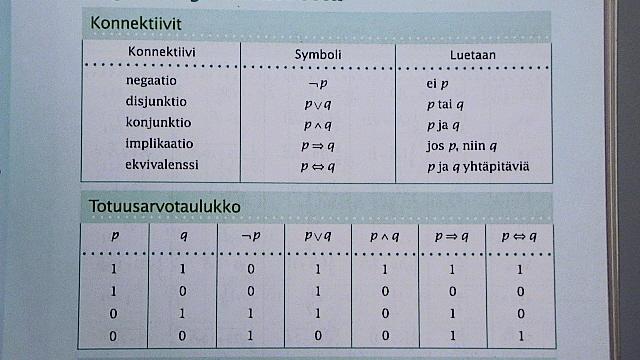
Totuustaulukko ilmaisee ns. formaalin matemaattisen lausekkeen totuusarvon. Formaalikielen lause on huomattavasti yksinkertaisempi kuin luonnollisen kielen lause, tällä kurssilla formaalit lauseet muodostetaan käyttämällä vain konnektiiveja (suhteita ilmaiseva sana)
EI, JA, TAI, JOS...NIIN, JOS JA VAIN JOS. Matem. logiikan formaali lause voi olla vain TOSI (true, t, 1) tai EPÄTOSI (false, f, 0).



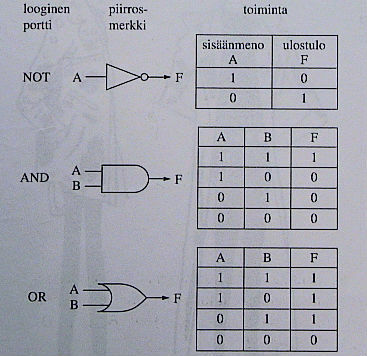
Tällaisenaankin totuustaulukkoja voidaan käyttää hyödyksi mm. elektroniikassa kun suunnitellaan virtapiirejä. Elektronisissa piireissäkin joko virta kulkee (TOSI, 1) tai ei kulje (EPÄTOSI, 0) joten ei tarvita monimutkaisempia totuusarvoja. Monimutkaisia elektronisia laitteita kootaan yksinkertaisista palasista, ns. loogisista piireistä jotka ovat juuri samoja kuin nuo yllä mainitut konnektiivit.


t. Pete

Totuustaulukon muodostaminen

0. MAOLssa on tarvittavien konnektiivien totuustaulukot.
Käytä näitä hyväksesi muodostaaksesi monimutkaisempien lauseiden totuustalukot



1. Formalisoi lause.

Esim. Pitkä matematiikka 11 teht. 17c:
A = "Annu osaa ratkaista tehtävän" ja B = "Eino osaa ratkaista tehtävän".
Silloin lause C = "Annu osaa mutta Eino ei osaa" voidaan formalisoida muotoon [[$ A\wedge \neg B $]]. Missä tilanteissa lause C on tosi?

2. Listaa taulukkoon kaikki tarvittavien lauseiden totuusarvot.
Esimerkissä tarvitaan vain A ja B, joten taulukkoon tulee vain kaksi saraketta ja neljä riviä vastaten kaikkia A:n ja B:n eri kombinaatioita (joita on siis aina [[$ 2^n $]] kpl). Jos lausekkeita on enemmän kuin kaksi niin ole tarkkana että listaat kaikki eri kombinaatiot!
A B
1 1
1 0
0 1
0 0

3. Etene kohti lopullisen lauseen totuustaulukkoa vaiheittain.
Laskujärjestys: sulkeet -> negaatio --> konjunktio ja disjunktio --> implikaatio ja ekvivalenssi. Esimerkissä siis ensin "negaatio B" ja sitten vasta "A:n ja ei-B:n konjunktio".
A B ei-B A ja ei-B
1 1 0 0
1 0 1 1
0 1 0 0
0 0 1 0

4. Vasta kysymykseen (yleensä viimeisen sarakkeen perusteella).
Esimerkissä siis lause C on tosi rivillä kaksi eli kun A on tosi ja B epätosi eli kun "Annu osaa mutta Eino ei".