Lämpö
Lämpömäärä
Erilaiset aineet voivat sitoa lämpöenergiaa eri määriä. Tätä ominaisuutta kutsutaan ominaislämpökapasiteetiksi. Jonkin tietyn kappaleen sitoma lämpömäärä riippuu siis kappaleen materiaalista, kappaleen massasta ja lämpötilan muutoksesta. Tutkitaan veden lämmittämistä:
Lämmitetään kylpypaljua, jossa on 1600 litraa 10[[$ ^{\circ} $]]C vettä. Kuinka paljon tarvitaan energiaa lämmittämään vesi mukavan lämpöiseksi, eli 35 asteikseksi? Veden ominaislämpökapasiteetti on 4,2 [[$ \frac{kJ}{kg ^{\circ }C} $]]
Ratkaisu:
Kootaan tiedot
[[$ m = 1600~kg \\c=4,2 \frac{kJ}{kg ^{\circ }C} \\ \Delta t=35 ~^{\circ }C-10 ^{\circ }C=25 ^{\circ }C $]]
Sijoitetaan kaavaan
[[$$ \begin{split} Q&=mc \Delta t \\ Q&=1600~kg \cdot 4,2 \frac{kJ}{kg ^{\circ }C} \cdot 25 ^{\circ }C\\ Q&=168000 ~kJ\\ Q&=168~MJ \end{split} $$]]
Esimerkki 1:
Lämmitetään kylpypaljua, jossa on 1600 litraa 10[[$ ^{\circ} $]]C vettä. Kuinka paljon tarvitaan energiaa lämmittämään vesi mukavan lämpöiseksi, eli 35 asteikseksi? Veden ominaislämpökapasiteetti on 4,2 [[$ \frac{kJ}{kg ^{\circ }C} $]]Ratkaisu:
Kootaan tiedot
[[$ m = 1600~kg \\c=4,2 \frac{kJ}{kg ^{\circ }C} \\ \Delta t=35 ~^{\circ }C-10 ^{\circ }C=25 ^{\circ }C $]]
Sijoitetaan kaavaan
[[$$ \begin{split} Q&=mc \Delta t \\ Q&=1600~kg \cdot 4,2 \frac{kJ}{kg ^{\circ }C} \cdot 25 ^{\circ }C\\ Q&=168000 ~kJ\\ Q&=168~MJ \end{split} $$]]
Lämmönjohtumisteho
Tiedät varmasti, että lämpö johtuu metallissa paremmin kuin esimerkiksi puussa tai muovissa. Kun halutaan määrittää kuinka tehokkaasti lämpö johtuu jonkin materiaalin lävitse, tarvitaan seuraavat tiedot
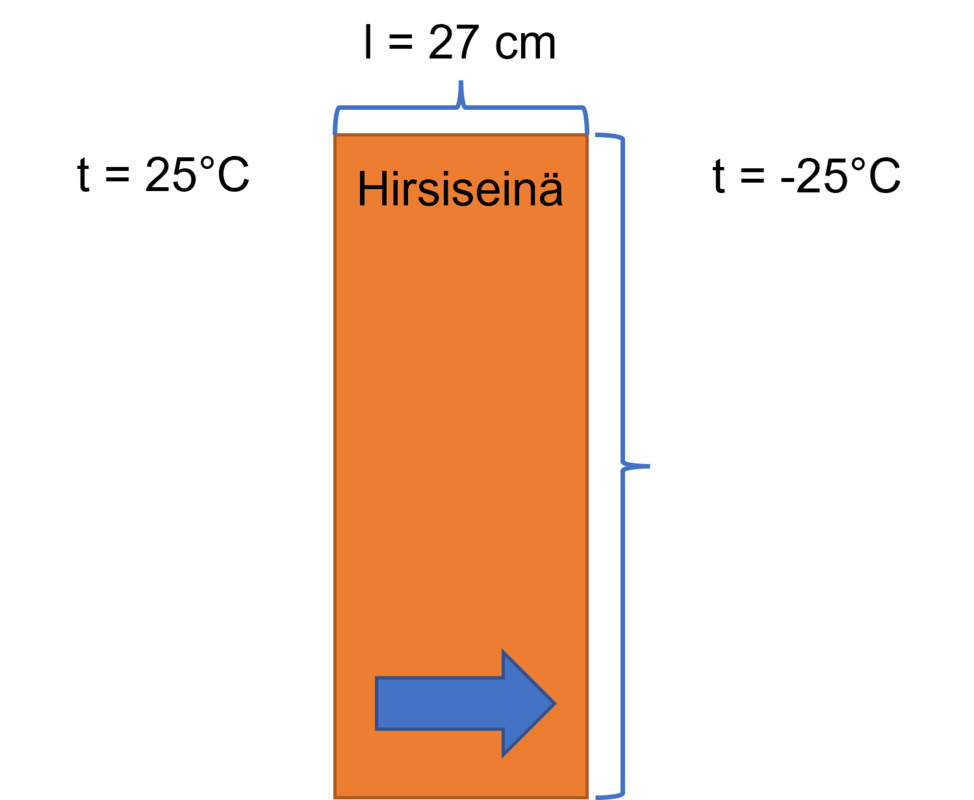Lamellihirsisen talon seinähirren paksuus on 27 cm. Sisällä on 25 °C lämmintä ja ulkona vastaavasti 25 °C pakkasta.
Kuinka suuri on lämmönjohtumisteho seinän läpi, kun sen korkeus
on 3 m ja leveys 5 m? Puun lämmönjohtavuus on 0,18 W/m°C
Ratkaisu:
Kootaan kaikki tiedot:
[[$ l = 0,27~m \\\Delta t=50~ ^{\circ }C \\ A=15~m^{2}\\ \lambda = 0,22~W/m^{\circ }C$]]
Sijoitetaan lämmönjohtumistehon yhtälöön:
[[$$ \begin{split} P&=0,18 \frac{W}{m^{\circ }C} \cdot 15~m^{2} \cdot \frac{50 ^{\circ }C}{0,27~m}\\ P&= 500~W \end{split} $$]]
- aineen lämmönjohtavuus - toiset aineet johtavat paremmin kuin toiset. Taulukkoarvo
- pinta-ala, jonka läpi lämpöä siirtyy
- materiaalikerroksen paksuus
- lämpötilaero materiaalin eri puolilla
Esimerkki 2:
Lamellihirsisen talon seinähirren paksuus on 27 cm. Sisällä on 25 °C lämmintä ja ulkona vastaavasti 25 °C pakkasta.Kuinka suuri on lämmönjohtumisteho seinän läpi, kun sen korkeus
on 3 m ja leveys 5 m? Puun lämmönjohtavuus on 0,18 W/m°C
Ratkaisu:
Kootaan kaikki tiedot:
[[$ l = 0,27~m \\\Delta t=50~ ^{\circ }C \\ A=15~m^{2}\\ \lambda = 0,22~W/m^{\circ }C$]]
Sijoitetaan lämmönjohtumistehon yhtälöön:
[[$$ \begin{split} P&=0,18 \frac{W}{m^{\circ }C} \cdot 15~m^{2} \cdot \frac{50 ^{\circ }C}{0,27~m}\\ P&= 500~W \end{split} $$]]
Lämmönkuljetusteho
Lämmönkuljetustehoa käytetään kuvaamaan sitä, kuinka paljon lämpöä aine pystyy kuljettamaan.
Esimerkkinä vesikiertoisen lämmityksen kiertovesi, joka kuljettaa lämmön koko lämmitettävään rakennukseen. Lämmönkuljetusteho määritetään laskemalla ensin aineen kyky sitoa lämpöä, eli lämpömäärä. Kun lämpömäärä jaetaan aineen kuljettamiseen käytetyllä ajalla, saadaan lämmönkuljetusteho.
Ratkaisu:
Otetaan tarkastelujaksoksi tunti. Listataan kaikki tiedot:
[[$ \Delta t = 1 h = 3600~ s\\ \Delta T = 80~^{\cdot}C - 40~^{\cdot}C = 40~^{\cdot}C\\ m = 15~kg\\ c = 4,2 \frac{kJ}{kg ^{\cdot}C}\\ $]]
Sijoitetaan yhtälöön:
[[$$ \begin{split}P&=\frac{mc \Delta T (LÄMPÖTILA)}{\Delta t (AIKA)}\\&=\frac{15~kg \cdot 4,2~\frac{kJ}{kg~^{\cdot}C} \cdot 40~^{\cdot}C}{3600~s}\\&=0,7~ kW \end{split}$$]]
Lämmönkuljetusteho on siis 700 W.
Esimerkkinä vesikiertoisen lämmityksen kiertovesi, joka kuljettaa lämmön koko lämmitettävään rakennukseen. Lämmönkuljetusteho määritetään laskemalla ensin aineen kyky sitoa lämpöä, eli lämpömäärä. Kun lämpömäärä jaetaan aineen kuljettamiseen käytetyllä ajalla, saadaan lämmönkuljetusteho.
Esimerkki 3:
Laske lämmityspatterin lämmönkuljetusteho. Patteriin virtaavan veden lämpötila on 80 °C ja siitä poistuvan veden lämpötila on 40 °C. Veden virtausnopeus on 15 l/h.Ratkaisu:
Otetaan tarkastelujaksoksi tunti. Listataan kaikki tiedot:
[[$ \Delta t = 1 h = 3600~ s\\ \Delta T = 80~^{\cdot}C - 40~^{\cdot}C = 40~^{\cdot}C\\ m = 15~kg\\ c = 4,2 \frac{kJ}{kg ^{\cdot}C}\\ $]]
Sijoitetaan yhtälöön:
[[$$ \begin{split}P&=\frac{mc \Delta T (LÄMPÖTILA)}{\Delta t (AIKA)}\\&=\frac{15~kg \cdot 4,2~\frac{kJ}{kg~^{\cdot}C} \cdot 40~^{\cdot}C}{3600~s}\\&=0,7~ kW \end{split}$$]]
Lämmönkuljetusteho on siis 700 W.