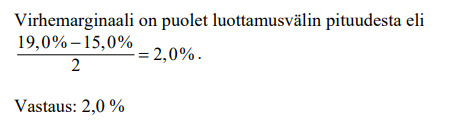esimerkkejä ratkaisuista

406.

402.

404.

$\overline{x}=33{,}9\ cm$
$s=1{,}2\ cm$

$n=4\ kpl$

a)

$s_{\overline{x}}=\frac{s}{\sqrt{n}}=\frac{1{,}2}{\sqrt{4}}=0{,}6$

Vastaus : 0,6

405.

[[$ \left[ \bar{x}-2,58\dfrac{s}{\sqrt{n}};\ \bar{x}+2,58\dfrac{s}{\sqrt{n}} \right] $]]

$\overline{x}=523\ cm$
$n=60$

$s=120$

$\left[523-2{,}58\frac{120}{\sqrt{60}};\ 523+2{,}58\frac{120}{\sqrt{60}}\right]=$

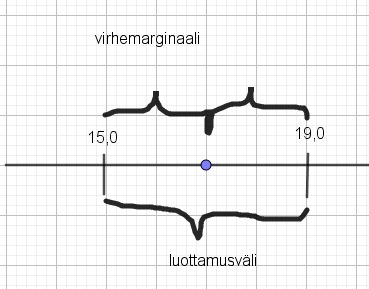
Pyöristys pitää luottamusvälissä aina tehdä kauemmas keskiarvosta, joten luottamusväli on kolmen merkitsevän numeron tarkkuudella

$\left[492{,}635...\ ;\ 553{,}364...\right]\approx\left[492\ ;\ 554\right]$

V: $\left[492\ ;\ 554\right]$

405.

Kaava löytyy MAOL:sta.

Ratkaistuna sähköisesti:

406.

n= 302
26 kpl käytti nikotiinivalmistetta

$\left[\hat{p}-1{,}96s;\ \hat{p}+1{,}96s\right]\ Kaava\ MAOL:ssa!$ Huom! Maolin kaavassa eri merkintä, kuin oppikirjassa.

$s=\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}=\ \ Kaava\ MAOL:ssa!$

Todennäköisyys, että otoksessa oleva käyttää nikotiinivalmistetta on siis
$p=\frac{26}{302}=0{,}08609271523178807947$

$\left[\hat{p}-1{,}96s;\ \hat{p}+1{,}96s\right]$

$\left[0{,}08609271523178807947-1{,}96s\ ;\ 0{,}08609271523178807947+1{,}96s\right]$ Pitää laske s!

$s=\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}=\ \ Kaava\ MAOL:ssa!$
$s=\sqrt{\frac{0{,}08609271523178807947\cdot(1-0{,}08609271523178807947)}{302}}$ = 0,0161410....

Lasku laitettu speedcrunchiin:
sqrt(0{,}08609271523178807947*(1-0{,}08609271523178807947)/302)

= 0,0161410134938494557

$\left[0{,}08609271523178807947-1{,}96s\ ;\ 0{,}08609271523178807947+1{,}96s\right]$ =
[0,05436... ; 0,1176...]
$\approx\left[0{,}054\ ;\ 0{,}12\ \right]$

V: Luottamusväli noin $\approx\left[0{,}054\ ;\ 0{,}12\ \right]$

408

411.

[[$ \left[ \bar{x}-3,29\dfrac{s}{\sqrt{n}};\ \bar{x}+3,29\dfrac{s}{\sqrt{n}} \right] $]] tehtävässä ei ole kerrottu keskihajontaa tai otoksen kokoa, joten ei onnistu tällä tavoin.

Otoksen keskiarvo on luottamusvälin rajojen keskiarvo, joten otoksen keskiarvo on

$\frac{10{,}1+14{,}3}{2}=12{,}2$

(Lasku speedcrunchilla:(10,1+14,3)/2

= 12,2)

V: $\overline{x}=12{,}2$

412.

a) n=100
$\overline{x}=66\ mm$
$s=1\ mm$

Muuttujana on n=100 kappaleen otosten keskiarvo. Keskiarvon keskihajonta saadaan keskiarvon keskivirheen kaavalla (kuinka paljon kesmäärin poikkeaa keskiarvosta). Perusjoukon keskihajonta on s=1 mm, joten

$s_{\overline{x}}=\frac{s}{\sqrt{n}}$
$s_{\overline{x}}=\frac{1mm}{\sqrt{100}}=0{,}1\ mm$

$V:\ 0{,}1\ mm$