Uusinta 12.1.2023

1.

Tässä tehtävässä joudut tekemään paljon laskuja!

1.1
Fasaanien lukumäärä voi olla vain positiivinen kokonaisluku eli on diskreetti.

1.2.
P(viallinen)=2%=0,02
P(ehjä)=1-0,02=0,98

VEEEE vain 1. on viallinen eli järjestyksellä on väliä. 0,018

$0{,}02\cdot0{,}98^4=0{,}018447...\approx0{,}018$

1.3.
Normota arvot, jotta voit vertailla niitä.

matematiikka:
$\overline{x}=7{,}2$
$s=1{,}5$
$x=8$
$z=\frac{x-\overline{x}}{s}=\frac{8-7{,}2}{1{,}5}=0{,}5333...$ suurempi, kuin historian normitettu arvo eli selviytyi paremmin matematiikassa.
$Historia$
$\overline{x}=8{,}1$
$s=1{,}9$
$x=9$
$z=\frac{x-\overline{x}}{s}=\frac{9-8{,}1}{1{,}9}=0{,}4736...\approx0{,}47$
$historian\ arvosana\ 10\ onko\ yhtä\ kaukana\ keskiarvostakuin\ matematiikan\ arvosana\ 8?$
$z=\frac{10-8{,}1}{1{,}9}=1\ne0{,}533...\ 10\ olisi\ suhteellisesti\ parempi\ kuin\ matematiikan\ 8.$

Oikea vaihtoehto on 0,47

1.4
Lasketaan väli
7,5-0,5=7,0 7,5 7,5+0,5=8,0
|________________|_________________|

[7,0h ; 8,0h]

1.5
p(viall)=2%=0,02
p(ehjä)=1-0,02=0,98
n=5 kpl
P(otoksessa on ainakin 1 viallinen)=1-P(kaikki ovat ehjiä)=

$1-0{,}98^5=0.0960792032\approx0{,}096$

0,096

1.6
poissonjakauma

2.

2.1
vuosi 4000 eaa.
$\overline{x}=161\ cm$
$s=5\ cm$

x=175 cm

$z_{4000eaa}=\frac{x-\overline{x}}{s}=\frac{175-161}{5}=2{,}8$

vuosi 2010

$\overline{x}=181\ cm$
$s=6\ cm$

x=175 c

$z_{2010}=\frac{x-\overline{x}}{s}=\frac{175-181}{6}=-1$

3.

Arviot olivat 5, 0, 2, 5, 1 ja 5.

eli 0,1,2,5,5,5,

3.1
Moodi on tyypillisin arvo eli 5, koska se esiintyi aineistossa useimmin eli 3 kertaa.

3.2.
$\overline{x}=\frac{\sum_1^5f_{_i\cdot x_i}}{n}=\frac{0+1+2+3\cdot5}{1+1+1+3}=\frac{18}{6}=3$

keskiarvo on 3.

3.3.
0,1,2,5,5,5,
aineiston keskimmäiset arvot ovat 2 ja 5, niiden keskiarvo on 3,5

(2+5)/2

= 3.5

Mediaani on suuruusjärjestykseen kirjoitetun aineiston keskimmäinen arvo tai kahden keskimmäisen arvon keskiarvo.
Md=3,5

3.4.
Laske aineiston keskihajonta.

$\begin{matrix} x&f&f\left(x-\overline{x}\right)^2\\ 0&1&1\cdot\left(0-3\right)^2\\ 1&1&1\cdot\left(1-3\right)^2\\ 2&1&1\cdot\left(2-3\right)^2\\ 5&3&3\cdot\left(5-3\right)^2\\ && \end{matrix}$

$\overline{x}=3$

otoskeskihajonta:

$s_{n-1}=\sqrt{\frac{1\cdot\left(0-3\right)^2+1\cdot\left(1-3\right)^2+1\cdot\left(2-3\right)^2+3\cdot\left(5-3\right)^2}{6-1}}=2{,}28035\approx2{,}28$

tai

keskihajonta:
$s_n=\sqrt{\frac{1\cdot\left(0-3\right)^2+1\cdot\left(1-3\right)^2+1\cdot\left(2-3\right)^2+3\cdot\left(5-3\right)^2}{6}}=2{,}08167\approx2{,}08$

4.

Tehtävä oli oppikirjan esimerkki.

5.

Työmatkallasi on viisi valoristeystä. Vihreä valo palaa keskimäärin 25 sekuntia minuutissa, koska risteävä liikenne tarvitsee myös vihreää valoa. Millä todennäköisyydellä ainakin kahdessa valoristeyksessä sinua odottaa vihreät valot?

$P\left(punainen\right)=1-\frac{25\ }{60}\ =\frac{60-25}{60}=\frac{35}{60}=\frac{7}{12}$ Laskuissa kannattaa käyttää tarkkaa murtolukumuotoa, likimääräisen
$=0.583333333333...$ desimaaliarvon sijaan.
$P\left(vihreä\right)=\frac{25\ sek}{60\ sek}=\frac{5}{12}=$
$0.41666666666$

P(ainakin kahdessa valoristeyksessä sinua odottaa vihreät valot)= 1 - P(nollassa [[$ \color{blue} {tai} $]] yhdessä risteyksessä on vihreä valo) =
1 - 0,30877 = 0.69122942

Laske erikseen:
P( nollassa [[$ \color{blue} { tai } $]] yhdessä risteyksessä on vihreä valo)
= 0.06754356352880658436 [[$ \color{blue} { + } $]] 0.24122701260288 =0,3088

sijoita tämä summa yläpuolella olevaan laskuusi.

Geogebralla ja speedcrunchilla tehdyt laskut:(geogebra laskee tarkemmilla arvoilla, kuin laskuissa ilmoittaa, koska käytetyt arvot on kopioitu ei itse kirjoitettu)

P(nolla vihreää valoa)=P(kaikissa viidessä valossa palaa punainen)= P(punainen ja punainen ja punainen ja punainen ja punainen valo)=
$\left(\frac{7}{12}\right)^5=0.06754356352880658436$
P(yhdessä risteyksessä palaa vihreä valo (mikä tahansa risteys voi olla kyseessä!))= $\binom{5}{1}\cdot\left(\frac{5}{12}\right)\cdot\left(\frac{7}{12}\right)^4=0.24122701260288065844$

Vastaus: 0.69

6.

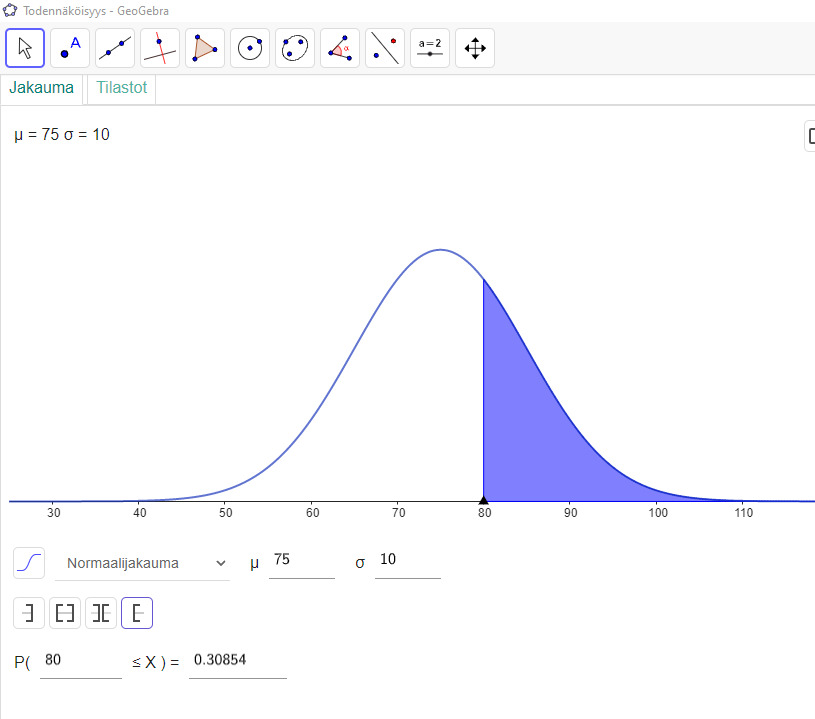
Suuren hampurilaisravintolaketjun sekunnissa maailmassa myymien hampurilaisten määrä noudattaa normaalijakaumaa N(75, 10). Oletetaan, että peräkkäisinä sekunteina myytyjen hampurilaisten määrät ovat toisistaan riippumattomia.

6.1 Millä todennäköisyydellä ketju myy satunnaisesti valitun sekunnin aikana yli 80 hampurilaista? (6p)

6.2 6 p.

Millä todennäköisyydellä ketju myy satunnaisesti valitun 10 sekunnin aikana yli 800 hampurilaista?