2.1 Toistokoe
Matikkamatskut toistokoe video
Binomitodennäköisyys
Esimerkki 1.
Koripalloilija onnistuu yksittäisessä vapaaheitossa 70%:n todennäköisyydellä. Millä todennäköisyydellä kolmesta heitosta täsmälleen kaksi onnistuu.
Ratkaisu:
Heitolla on kaksi mahdollista vaihtoehtoa, se joko onnistuu tai ei onnistu.
O=onnistuu P(O)=0,70
E= ei onnistu P(E)=1-0,70=0,30
Taulukoi kaikki erilaiset järjestykset onnistua:
Erilaisia järjestyksiä on kolme, jokaisen järjestyksen todennäköisyys on sama. [[$0{,}7\cdot0{,}7\cdot0{,}3+0{,}7\cdot0{,}3\cdot0{,}7+0{,}7\cdot0{,}3\cdot0{,}7=3\cdot0{,}7^2\cdot0{,}3^1=\binom{3}{2}0{,}7^2\cdot0{,}3=0{,}441 $]]
Kolme (3) heittoa, ( [[$ \color{blue}{täsmälleen \ 2} $]]) onnistuu
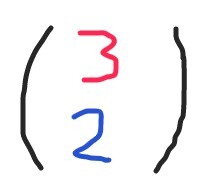

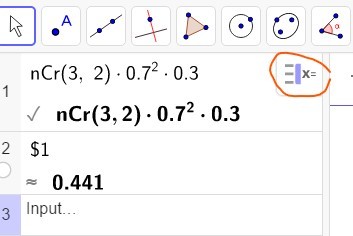
Ratkaisu:
Heitolla on kaksi mahdollista vaihtoehtoa, se joko onnistuu tai ei onnistu.
O=onnistuu P(O)=0,70
E= ei onnistu P(E)=1-0,70=0,30
Taulukoi kaikki erilaiset järjestykset onnistua:
| 1. heitto | 2. heitto | 3. heitto | |
| O | O | E | 0,7*0,7*0,3=0,147 |
| O | E | O | 0,7*0,3*0,7=0,147 |
| E | O | O | 0,3*0,7*0,7=0,147 |
Erilaisia järjestyksiä on kolme, jokaisen järjestyksen todennäköisyys on sama. [[$0{,}7\cdot0{,}7\cdot0{,}3+0{,}7\cdot0{,}3\cdot0{,}7+0{,}7\cdot0{,}3\cdot0{,}7=3\cdot0{,}7^2\cdot0{,}3^1=\binom{3}{2}0{,}7^2\cdot0{,}3=0{,}441 $]]
Kolme (3) heittoa, ( [[$ \color{blue}{täsmälleen \ 2} $]]) onnistuu


Esim. 2
(B) Kukkalajikkeen siemenpussin kyljessä lukee, että 76% siemenistä itää.
Millä todennäköisyydellä neljä tai viisi siementä viidestä itää?
Ratkaisu:
Käytä binomitodennäköisyyttä
n=5
p(itää)= 76%=0,76
p(ei idä)= 1- 0,76
tasan 4 siementä itää: k=4
tasan 5 siementä itää: k=5
P(4 siementä viidestä siemenestä itää tai viisi viidestä siemenestä itää)= Yhteenlaskusääntö
P(4 siementä viidestä siemenestä itää) + P(viisi viidestä siemenestä itää)=
V: Noin 65 %:n todennäköisyydellä
Esim. 3
(B) Eräässä kanamunien myyntierässä havaittiin, että 5% kotelossa olevista munista oli pilaantunut. Millä todennäköisyydellä satunnainen ostaja ottaa 6 kappaleen kananmunakotelon, jossa ainakin
kaksi munaa on pilaantunut?
Ratkaisu:
ainakin kaksi munaa on pilaantunut = kaksi, kolme, neljä viisi tai kuusi munaa on pilaantunut
Munia on kotelossa 6 kpl
Vaihtoehdot pilaantuneiden määrästä on
%5C%20%3D%5C%201%5C%20%5C%20%5C)
Tässä todennäköisyys, että 0,1,2,3,4,5 tai 6 munaa on pilaantunut. Tapahtuma on VARMA.
Ainakin kaksi munaa on pilaantunut tapahtuman komplementti on 0 tai yksi muna on pilaantunut.
Lasketaan ensin todennäköisyys
)
%2BP%5Cleft(yksi%5C%20muna%5C%20on%5C%20pilaantunut%5Cright)%3D)
V: Todennäköisyys, että ainakin kaksi munaa on pilaantunut on noin 3%
kaksi munaa on pilaantunut?
Ratkaisu:
ainakin kaksi munaa on pilaantunut = kaksi, kolme, neljä viisi tai kuusi munaa on pilaantunut
Munia on kotelossa 6 kpl
Vaihtoehdot pilaantuneiden määrästä on
| pilaantuneita | ||
| 0 | ei suotuisa | P(0 pilaantunutta)= |
| 1 | ei suotuisa | |
| 2 | suotuisa | |
| 3 | suotuisa | |
| 4 | suotuisa | |
| 5 | suotuisa | |
| 6 | suotuisa |
Tässä todennäköisyys, että 0,1,2,3,4,5 tai 6 munaa on pilaantunut. Tapahtuma on VARMA.
Ainakin kaksi munaa on pilaantunut tapahtuman komplementti on 0 tai yksi muna on pilaantunut.
Lasketaan ensin todennäköisyys
0,735091890625+0,23213428125 = 0,967226171875
Sen jälkeen vähennät tämän arvon yhdestä:
1-0,967226171875 = 0,032773828125 noin 3 %
V: Todennäköisyys, että ainakin kaksi munaa on pilaantunut on noin 3%
218.
Yhdessä

