Esimerkki 1.
Koripalloilija onnistuu yksittäisessä vapaaheitossa 70%:n todennäköisyydellä. Millä todennäköisyydellä kolmesta heitosta täsmälleen kaksi onnistuu.
Ratkaisu:
Heitolla on kaksi mahdollista vaihtoehtoa, se joko onnistuu tai ei onnistu.
O=onnistuu P(O)=0,70
E= ei onnistu P(E)=1-0,70=0,30
Taulukoi kaikki erilaiset järjestykset onnistua:
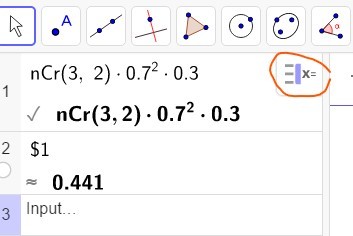
Erilaisia järjestyksiä on kolme, jokaisen järjestyksen todennäköisyys on sama. [[$0{,}7\cdot0{,}7\cdot0{,}3+0{,}7\cdot0{,}3\cdot0{,}7+0{,}7\cdot0{,}3\cdot0{,}7=3\cdot0{,}7^2\cdot0{,}3^1=\binom{3}{2}0{,}7^2\cdot0{,}3=0{,}441 $]]
Kolme (3) heittoa, ( [[$ \color{blue}{täsmälleen \ 2} $]]) onnistuu
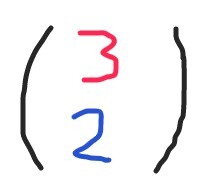

Ratkaisu:
Heitolla on kaksi mahdollista vaihtoehtoa, se joko onnistuu tai ei onnistu.
O=onnistuu P(O)=0,70
E= ei onnistu P(E)=1-0,70=0,30
Taulukoi kaikki erilaiset järjestykset onnistua:
| 1. heitto | 2. heitto | 3. heitto | |
| O | O | E | 0,7*0,7*0,3=0,147 |
| O | E | O | 0,7*0,3*0,7=0,147 |
| E | O | O | 0,3*0,7*0,7=0,147 |
Erilaisia järjestyksiä on kolme, jokaisen järjestyksen todennäköisyys on sama. [[$0{,}7\cdot0{,}7\cdot0{,}3+0{,}7\cdot0{,}3\cdot0{,}7+0{,}7\cdot0{,}3\cdot0{,}7=3\cdot0{,}7^2\cdot0{,}3^1=\binom{3}{2}0{,}7^2\cdot0{,}3=0{,}441 $]]
Kolme (3) heittoa, ( [[$ \color{blue}{täsmälleen \ 2} $]]) onnistuu

