2.2. Binomijakauma ja Poisson jakauma
Esim. 1 sivu 44
Yhdellä pelikierroksella saatu voitto on sattuman määräämä eli satunnaismuuttuja.
Merkitään sitä kirjaimella [[$ {\color{blue} {X }} $]] . Satunnaismuuttujan [[$ {\color{blue} {X }} $]] mahdolliset arvot x saadaan , kun huomioidaan, että jokainen pelikierros maksaa 2 €. Lisätään arvot taulukkoon ja muodostetaan satunnaismuuttujan [[$ {\color{blue} {X }} $]] todennäköisyysjakauma.

Satunnaismuuttuja [[$ {\color{blue} {X }} $]] odotusarvo saadaan kertomalla kukin voitto todennäköisyydellään ja laskemalla tulot yhteen.
[[$ \mu=\Sigma px=0{,}30\cdot0+0{,}10\cdot2+0{,}01\cdot73+0{,}59\cdot\left(-2\right)=-0{,}25 $]]
Koska voiton odotusarvo on negatiivinen eli -0,25 euroa, ei pelaaminen ole pitkällä aikavälillä kannattavaa.
Merkitään sitä kirjaimella [[$ {\color{blue} {X }} $]] . Satunnaismuuttujan [[$ {\color{blue} {X }} $]] mahdolliset arvot x saadaan , kun huomioidaan, että jokainen pelikierros maksaa 2 €. Lisätään arvot taulukkoon ja muodostetaan satunnaismuuttujan [[$ {\color{blue} {X }} $]] todennäköisyysjakauma.

Satunnaismuuttuja [[$ {\color{blue} {X }} $]] odotusarvo saadaan kertomalla kukin voitto todennäköisyydellään ja laskemalla tulot yhteen.
[[$ \mu=\Sigma px=0{,}30\cdot0+0{,}10\cdot2+0{,}01\cdot73+0{,}59\cdot\left(-2\right)=-0{,}25 $]]
Koska voiton odotusarvo on negatiivinen eli -0,25 euroa, ei pelaaminen ole pitkällä aikavälillä kannattavaa.
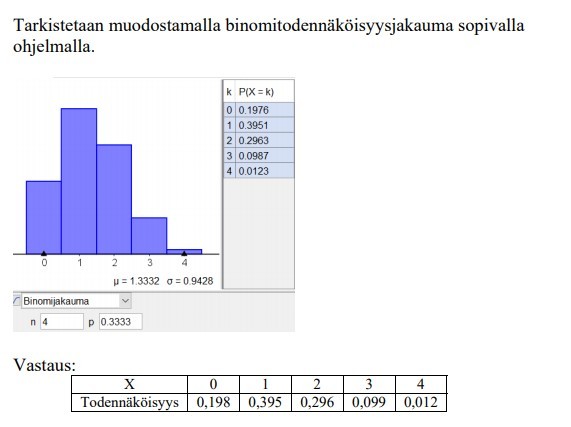
Binomijakauma
Poissonjakauma
Binomijakauman odotusarvo ja keskihajonta sähköisesti
230.
Binomijakauman teko Geogebran todennäköisyyslaskurilla
Tehtävä 230
Poisson-jakauma
Kun tapahtumakertojen lukumäärää ei tiedetä, käytetään Poisson jakaumaa.

Jos toistojen lukumäärää ei tiedetä (tai tapahtuma voi toistua kuinka monta kertaa tahansa), mutta tiedetään odotusarvo, voidaan käyttää Poisson-jakaumaa.
Video sivulta 49.
Poisson kaava MAOL:ssa


Jos toistojen lukumäärää ei tiedetä (tai tapahtuma voi toistua kuinka monta kertaa tahansa), mutta tiedetään odotusarvo, voidaan käyttää Poisson-jakaumaa.
Video sivulta 49.
Poisson kaava MAOL:ssa

Esim.4.

Ratkaisu:
Kaikkien asiakkaiden lukumäärää ei tiedetä, valitaan Poisson jakauma
a) k=3
e= 2,71828182845904
e on vakio!P(täsmälleen 3 asiakasta valittaa)=
Laskettu SpeedCrunchilla:
(6^3)/3!*e^(-6)
= 0,0892350783599
V:
b)
P(alle 3 asiakasta valittaa)=P(täsmälleen nolla asiakasta valittaa)+P(täsmälleen yksi asiakas valittaa)+P(täsmälleen 2 asiakasta valittaa)
[Käytetty yhteenlaskusääntöä!] =0,00247...+ 0,0148...+0,0446...=0,061968804416658960

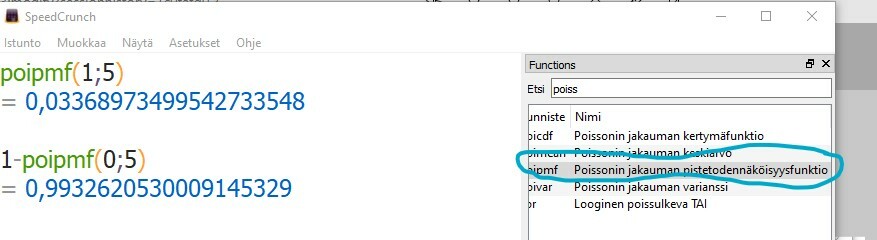
SpeedCrunchilla laskettuna:
(6^0)/0!*e^(-6)+(6^1)/1!*e^(-6)+(6^2)/2!*e^(-6)
= 0,06196880441665896058
0,00247875217666635842+0,01487251305999815054+0,04461753917999445161
= 0,06196880441665896057
Geogebran todennäköisyyslaskurilla:

c)
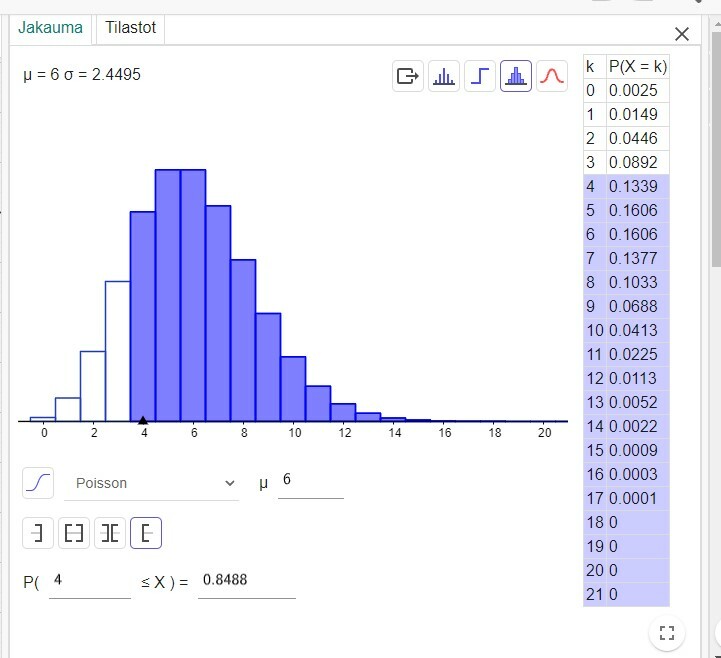
V: noin 84,9 %