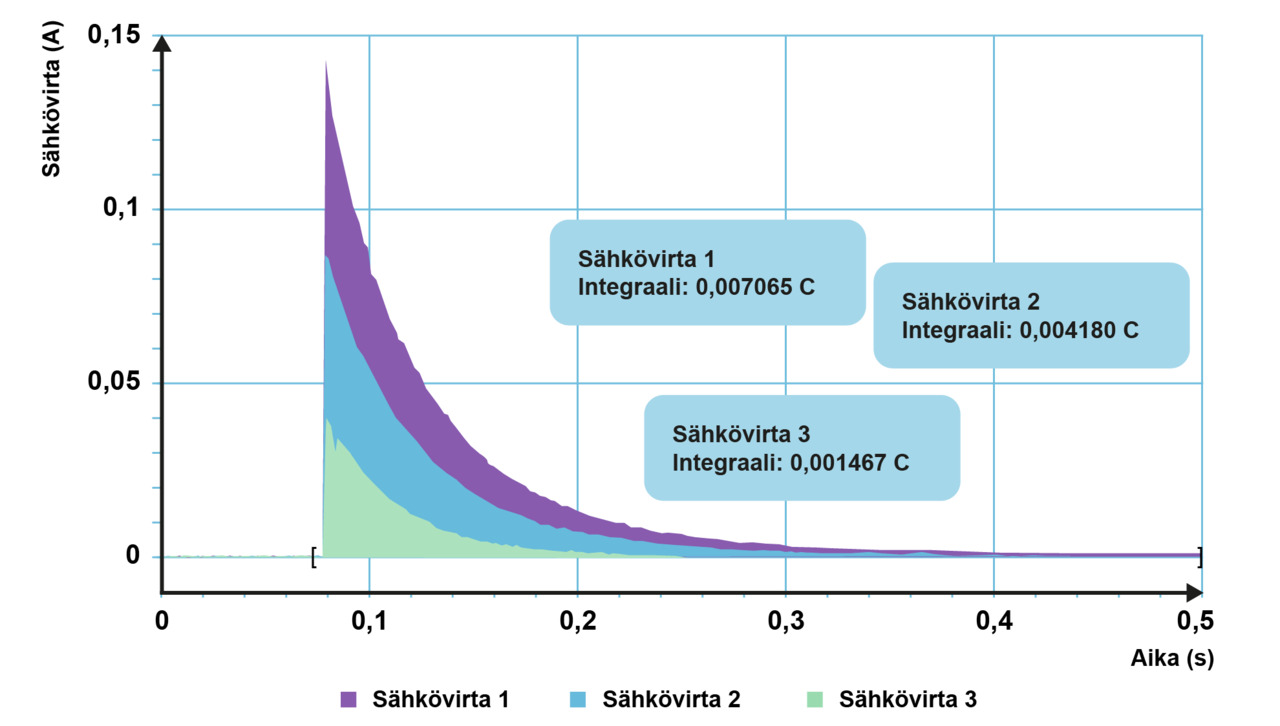
Kondensaattorin jännitteen suuruus riippuu pariston napajännitteestä. Mitä suurempi pariston napajännite on, sitä suuremmaksi myös kondensaattorin jännite tulee ja sitä enemmän varausta kondensaattoriin siirtyy. Purettaessa kondensaattoria suuremmasta määrästä varausta riittää sähkövirtaa pidemmäksi aikaa.

Alla kuvassa on sama kondensaattori varattu eri jännitteillä (1: 6,14 V, 2: 4,10 V, 3: 1,47 V). Mitä suurempaan jännitteeseen kondensaattoria varataan, sitä suurempi virta mitataan.

Kondensaattoriin siirtynyt varaus saadaan kussakin tapauksessa erikseen integroimalla sähkövirta.

Jännite	6,14 V	4,10 V	1,47 V
Varaus	0,00707 C	0,00418 C	0,00147 C

Eri jännitteisiin ladattujen kondensaattoreiden varaukset ovat sitä suurempia, mitä isompi on jännitelähteen napajännite. Alla on mittauspisteet kondensaattorin jännitteestä ja sen varauksesta kyseisellä jännitteellä useammasta eri mittauksesta. Mittauspisteet muodostavat origon kautta kulkevan suoran [[$\left(U,Q\right)$]]-koordinaatistossa, joten varaus on suoraan verrannollinen jännitteeseen.

Kondensaattorin varaus ja jännite

Jännite [[$U$]]	Varaus [[$Q$]]
1,47 V	0,00147 C
2,95 V	0,00298 C
4,10 V	0,00418 C
6,14 V	0,00707 C
7,22 V	0,00793 C

Varauksen ja jännitteen suhde määritetään suoran kulmakertoimesta. Mitä jyrkempi suora on, sitä enemmän varausta kondensaattoriin mahtuu tietyllä jännitteellä. Kulmakerroin kuvaa siten kondensaattorin kykyä varastoida sähkövarausta. Se on kondensaattorille ominainen vakio, kondensaattorin kapasitanssi [[$C$]]. Kapasitanssin yksikkö on faradi, F. Edellä tarkastellun kondensaattorin kapasitanssiksi saadaan 0,001 F eli 1 mF. Faradi on saanut nimensä sähkön ja magnetismin yhteyttä tutkineen englantilaisen Michael Faradayn (1791–1867) mukaan.

Michael Faraday (Wikipedia)​