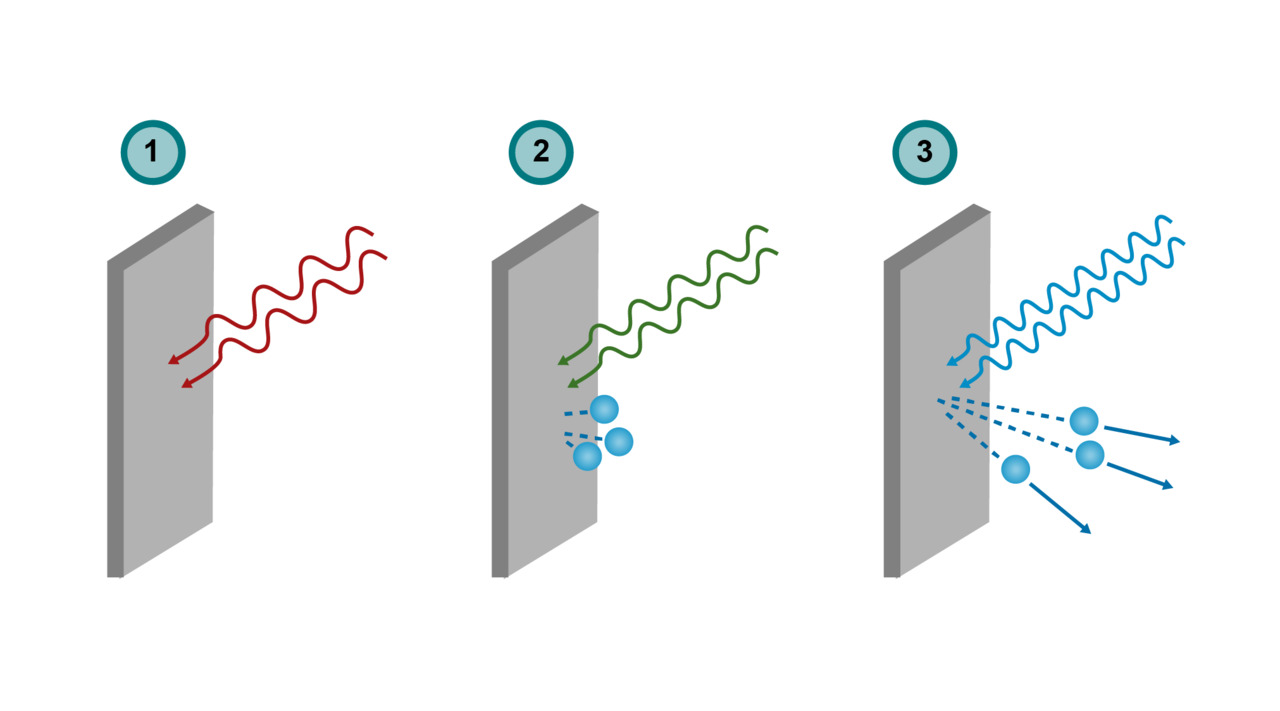
Tarkastellaan valosähköilmiötä edellä esitetyn kvanttihypoteesin ja energian säilymislain näkökulmasta. Säteily luovuttaa metallille energiaa yksittäisinä kvantteina. Jos taajuus on pieni, kvanttien energia on niin pieni, että niiden energia ei voi irrottaa elektroneja. Säteilyn taajuuden suurentaminen kasvattaa kvanttien energiaa, kunnes kvanttien energia mahdollistaa elektronien irrottamisen.

Rajataajuus, jolla elektroneja alkaa irrota, on jokaiselle metallille eri suuruinen. Rajataajuudella kvanttien energia on yhtä suuri kuin metallille ominainen irrotustyö, [[$W_0$]]. Irrotustöiden arvoja eri metalleille on taulukkokirjassa. Mikäli säteilyn taajuus on rajataajuutta suurempi, osa kvanttien energiasta muuntuu irtoavien elektronien liike-energiaksi [[$E_\text{k}$]].

Kuvasarjassa on eri taajuisen säteilyn ja aineen välinen vuorovaikutus. 1: Matalataajuuksinen säteily ei synnytä valosähköilmiötä. 2: Rajataajuudella elektroneja irtoaa ja valosähköilmiö tapahtuu, mutta elektroneilla ei ole liike-energiaa. 3: Suurella taajuudella irtoaa elektroneja, joilla on liike-energiaa.

Energian säilyminen valosähköilmiössä

Energian säilyminen valosähköilmiössä voidaan ilmaista seuraavalla yhtälöllä:

[[$ \qquad E_{\text{kvantti}}=W_0 +E_{\text{k}} $]]

Kvantin energia muuntuu irrotustyöksi ja elektronien liike-energiaksi. Yllä oleva yhtälö kirjoitetaan usein muodossa, jossa elekroneille jäävä liike-energia lasketaan kvantin energian ja irrotustyön erotuksena.

[[$ \qquad E_\text{k}=E_{\text{kvantti}}-W_0 $]]

Sähkökentän tekemä työ ja liike-energia

Yllä esitetyn yhtälön todentaminen on mahdollista mittalaitteistolla, jossa metallilevyyn kohdistetaan valoa ja irtoavien elektronien energia voidaan määrittää. Tähän soveltuva kytkentä on esitetty viereisessä kuvassa.


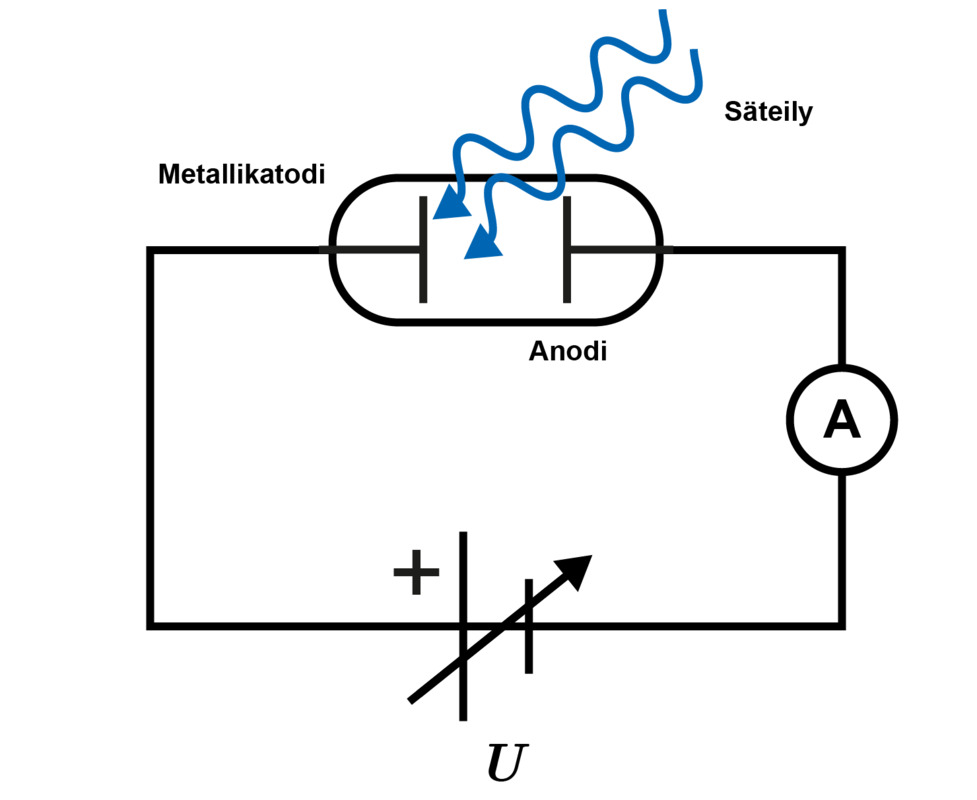
Katodi ja anodi on sijoitettu tyhjiöputkeen ja irtoavat elektronit synnyttävät sähkövirran virtapiiriin. Sähkövirta saadaan lakkaamaan kytkemällä virtapiiriin anodin ja katodin välille pysäytysjännite [[$U$]], jonka tuottama sähköinen voima vastustaa katodista irronneiden elektronien liikettä. Tällöin sähkökenttä tekee työtä elektronien liikkeen pysäyttämiseksi.

Sähkökentän tekemä työ:

[[$ \qquad W=Fs=QEs=QU $]]

Tutkimuksessa pysäytysjännite säädetään sellaiseksi, että sähkövirta piirissä lakkaa.

Tutkitaan kvanttien energian riippuvuutta säteilyn taajuudesta. Kohdistetaan katodiin säteilyä eri taajuuksilla ja määritetään irtoavien elektronien suurin liike-energia. Kun rajataajuus on ylitetty, elektronien liike-energian havaitaan kasvavan taajuuden suurentuessa. Liike-energian suuruus saadaan selville, kun elektronien virta juuri ja juuri lakkaa. Tällöin sähkökentän tekemä työ on yhtä suuri kuin elektronien liike-energia [[$QU=E_\text{k}$]].

Yksikkö elektronivoltti

Pysäytysjännitteen ollessa [[$U$]] irtoavien elektronien suurin energia on [[$QU$]], jossa [[$Q$]] on elektronin varaus eli alkeisvaraus. Kun alkeisvarausta merkitään tunnuksella e, saadaan elektronien energia yksikössä eV (elektronivoltti).

Energian perusyksikkö joule (J) on varsin suuri yksikkö säteilykvanttien energioihin nähden. Usein on käytännöllisempää käyttää energian yksikköä, elektronivolttia. Kun elektroni kiihdytetään sähkökentässä, jonka jännite on 1 V, sähkökentän tekemän työn kautta saadaan energian suuruudeksi [[$ 1 \ \mathrm{V}\cdot 1 \ \mathrm{e}=1 \ \mathrm{eV}$]]. Varaukseltaan yhtä suuri protoni saisi vastaavassa tilanteessa myös energian 1 eV.

Joulen ja elektronivoltin välinen muuntokerroin on alkeisvarauksen lukuarvo coulombeissa, ts. niiden välillä pätee seuraava yhtälö:

[[$ \qquad 1 \text{ eV} = 1{,}602176462 \cdot 10^{-19} \text{ J} $]]

Säteilykvantin energia

Erästä metallia tutkittaessa havaittiin elektronien suurimman liike-energian ja valon taajuuden välillä alla olevan kuvaajan mukainen riippuvuus.

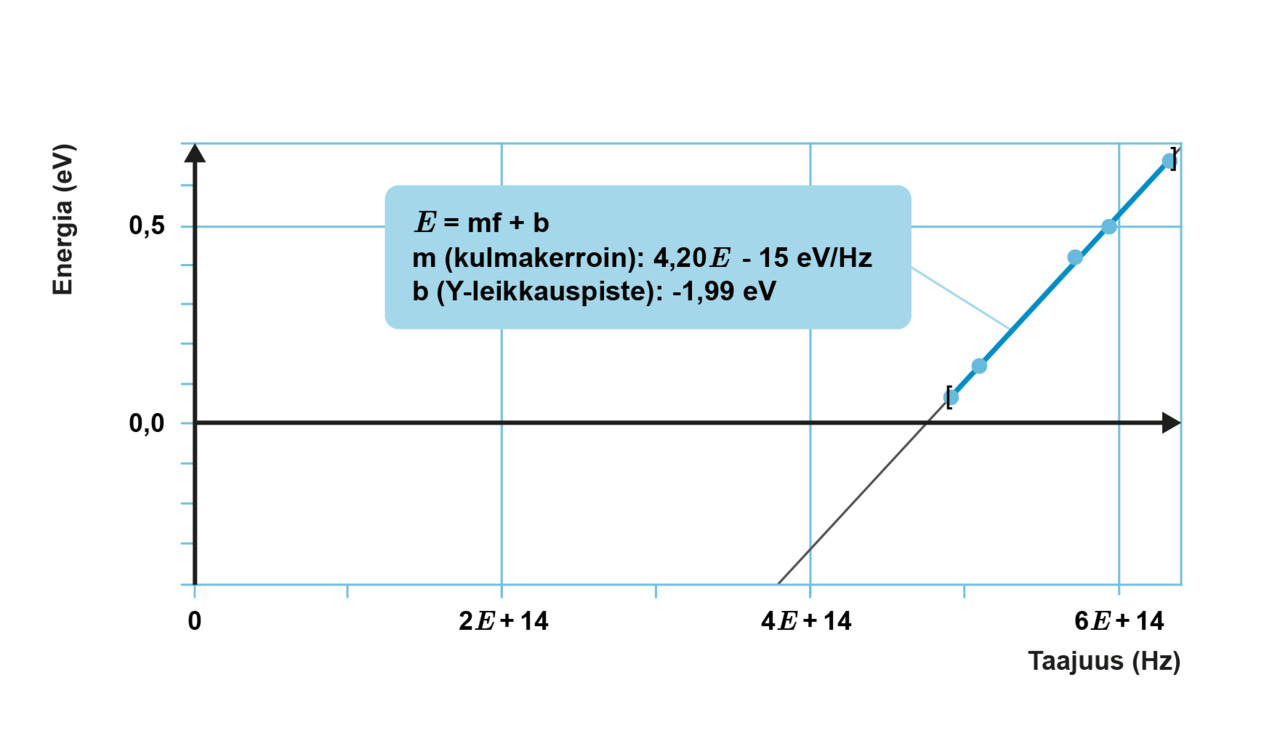
Pisteet asettuvat suoralle. Kvantin energia kasvaa lineaarisesti taajuuden suurentuessa. Ilmiötä kuvaa matemaattinen lauseke:

[[$ \qquad E_{\text{kvantti}}= \textrm{vakio}\cdot \textrm{taajuus} $]]

Kulmakerrointa kutsutaan Planckin vakioksi [[$h$]]. Se voidaan ilmoittaa joko yksikössä Js tai eVs.

[[$\qquad h=6{,}62606957\cdot 10^{-34}\text{ Js}=4{,}13566751\cdot 10^{-15}\text{ eVs}$]]

Säteilykvantin energian yksikkö on joko joule tai elektronivoltti. Energian yksikkö määräytyy sen mukaan, kumpaa yksikköä Planckin vakiolle käytetään.

[[$ \qquad\begin{align*}E&=hf=6{,}626 \cdot 10^{-34} \text{ Js}\cdot 1{,}4 \cdot 10^{15}\text{ Hz}\approx 9{,}3 \cdot 10^{-19}\text{ J} \\ \\ E&=hf=4{,}136 \cdot 10^{-15} \text{ eVs}\cdot 1{,}4 \cdot 10^{15}\text{ Hz} \approx 5{,}8\text{ eV} \end{align*}$]]

Valosähköilmiön matemaattinen malli

Suoran yhtälössä [[$y=kx+b$]] muuttujia ovat [[$x$]] ja [[$y$]]. Suoran kulmakerroin [[$k$]] on vaaka-akselin muuttujan kerroin, ja vakiotermi [[$b$]] on suoran ja pystyakselin leikkauskohta. Esitetään suoran yhtälö muodossa, jossa kvantin energia ilmoitetaan taajuuden ja Planckin vakion avulla.

[[$ \qquad E_\text{k}=hf-W_0 $]]

Kaavassa taajuus [[$f$]] ja energia [[$E_\text{k}$]] ovat muuttujia. Kvantin energian ja taajuuden välinen verrannollisuuskerroin on Planckin vakio, [[$h$]], joka luetaan suoran kulmakertoimesta. Se on mittauksessa [[$ 4{,}2 \cdot 10^{-15} \text { eVs} $]]​. Metallin irrotustyö on suoran ja energia-akselin leikkauskohta. Yhtälössä se on vakiotermi, jonka suuruus tutkimuksessa käytetylle metallille on [[$1{,}99 \text{ eV}$]].

Simulaatio: valosähköilmiö

Valosähköilmiön sovellus on aurinkopaneeli, jossa auringon säteilyn energiaa muunnetaan sähköksi.