2. Työ ja teho
Työ ja teho
Työ
Arkielämässä työ tarkoittaa jotakin, jonka tekemisestä maksetaan palkkaa. Kulutat omaa energiaasi ja saat vastineeksi rahaa. Mitä enemmän energiaasi kulutat, sitä enemmän (toivottavasti) saat palkkaa.
Fysiikassa tehdään työtä, kun energiaa muutetaan muodosta toiseen. Esimerkiksi sähköliesi tekee työtä, kun se muuttaa sähköenergian lämmöksi. Tässä kappaleessa keskitymme työhön, jossa energia kuluu kappaleiden liikuttamiseen.
Kappaleen liikuttaminen paikasta toiseen vaatii energiaa, joka muuttuu jostakin energiamuodosta liike-energiaksi. Esimerkiksi auton moottori tekee työtä, jossa polttoaineen kemiallinen energia muuttuu auton liikkeeksi.
Maanviljely on raskasta työtä ilman koneellista apua.
Tehdyn työn määrä kappaletta siirrettäessä riippuu kahdesta tekijästä: kappaleen siirtämiseen vaadittavasta voimasta ja matkasta, jonka kappale siirtyy.
Työn tunnus on [[$W$]] (engl. work) ja yksikkö on joule ([[$J$]]).
Voiman tekemä työ siirrettäessä
Kun kappaletta siirretään pintaa pitkin, niin siirtämiseen vaadittavan voiman [[$F$]] määrää kappaleen ja pinnan välinen kitka. Mitä suurempi kitka kappaleen ja pinnan välillä on, niin sitä suurempi on tarvittava voima.
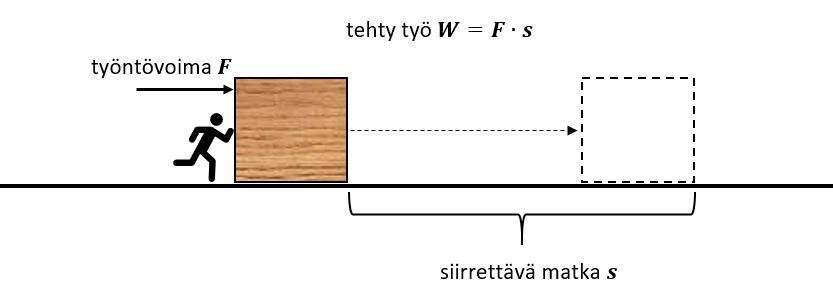
Kun kappaletta siirretään pintaa pitkin, niin tehty työ [[$W$]] lasketaan tarvittavan voiman [[$F$]] ja siirrettävän matkan [[$s$]] avulla kaavalla [[$$W=F \cdot s,$$]] missä voiman [[$F$]] yksikkö on newton ja matkan [[$s$]] yksikkö on metri.
Nostossa tehty työ
Kun kappaletta nostetaan, niin nostamiseen vaadittavan voiman määrää kappaleen paino. Mitä enemmän kappale painaa, niin sitä enemmän on tehtävä työtä sen nostamiseksi.
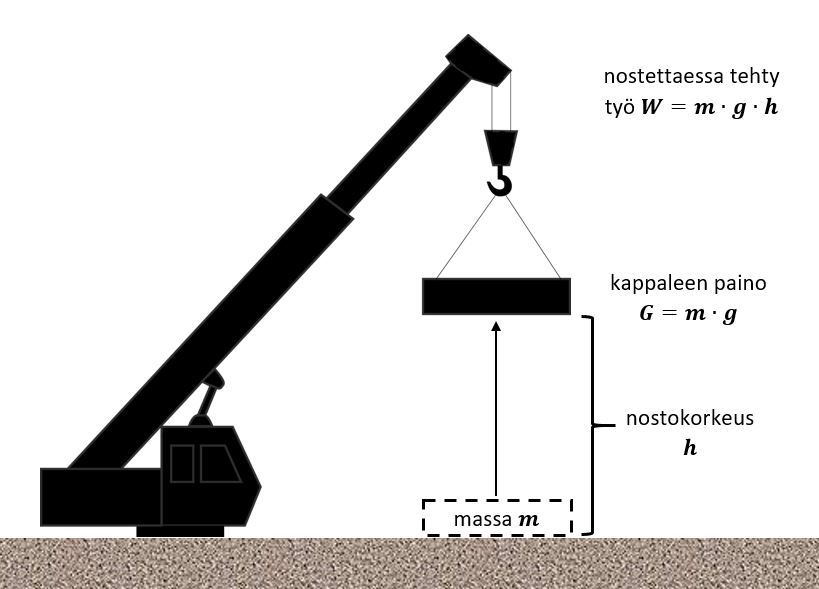
Kun kappaletta nostetaan, niin tehty työ [[$W$]] lasketaan kappaleeseen kohdistuvan painovoiman [[$G=m \cdot g$]] ja nostokorkeuden [[$h$]] avulla kaavalla [[$$ \begin{align} W&=G \cdot h \\ &=m \cdot g \cdot h, \end{align} $$]] missä [[$m$]] on kappaleen massa kilogrammoina, [[$g \approx10 \frac{m}{s^2} $]] on putoamiskiihtyvyys ja [[$h$]] on nostokorkeus metreinä.
Teho
Kiihdytyskilpailuissa yleensä tehokkain auto voittaa, sillä mitä enemmän autossa on tehoa, niin sitä lyhyemmässä ajassa auto ajaa kiihdytysuoran alusta loppuun.
Tehokkaampi auto on todennäköisempi voittaja kiihdytysajoissa.
Fysiikassa teho kuvaa työntekonopeutta. Mitä nopeammin jokin työ tehdään, niin sitä suurempi on teho.
Tehon tunnus on [[$P$]] (engl. power) ja yksikkö on watti ([[$W$]]).
(Etenkin moottoriajoneuvoissa tehon yksikkönä käytetään hevosvoimaa [[$hp$]] (engl. horsepower). Yksi hevosvoima on noin [[$736$]] wattia.)
Teho [[$P$]] lasketaan tehdyn työn [[$W$]] ja työhön käytetyn ajan [[$t$]] avulla kaavalla [[$$P=\frac{W}{t},$$]] missä ajan yksikkönä on sekunti.
Hyötysuhde
Auton moottori tekee työtä muuttaessaan polttoaineen sisältämää kemiallista energiaa liike-energiaksi. Polttoaineen sisältämä energia ei kuitenkaan muutu kokonaan renkaiden liikkeeksi, vaan osa energiasta kuluu moottorin synnyttämään lämpöön ja ääneen. Myös hehkulampun kuluttamasta sähköenergiasta suuri osa menee "hukkaan" hehkulampun synnyttämän lämmön takia.
Laitteen hyötysuhde ilmoittaa kuinka monta prosenttia kone tuottaa hyödyllistä energiaa.
Esimerkiksi sähkövoimalan hyötysuhde voi olla [[$80 \%$]]. Tällöin voimalan polttoaineen sisältämästä energiasta [[$80 \%$]] saadaan muutettua sähköksi ja loput [[$20 \%$]] "menee harakoille".
Arkielämässä työ tarkoittaa jotakin, jonka tekemisestä maksetaan palkkaa. Kulutat omaa energiaasi ja saat vastineeksi rahaa. Mitä enemmän energiaasi kulutat, sitä enemmän (toivottavasti) saat palkkaa.
Fysiikassa tehdään työtä, kun energiaa muutetaan muodosta toiseen. Esimerkiksi sähköliesi tekee työtä, kun se muuttaa sähköenergian lämmöksi. Tässä kappaleessa keskitymme työhön, jossa energia kuluu kappaleiden liikuttamiseen.
Kappaleen liikuttaminen paikasta toiseen vaatii energiaa, joka muuttuu jostakin energiamuodosta liike-energiaksi. Esimerkiksi auton moottori tekee työtä, jossa polttoaineen kemiallinen energia muuttuu auton liikkeeksi.
Maanviljely on raskasta työtä ilman koneellista apua.Tehdyn työn määrä kappaletta siirrettäessä riippuu kahdesta tekijästä: kappaleen siirtämiseen vaadittavasta voimasta ja matkasta, jonka kappale siirtyy.
Työn tunnus on [[$W$]] (engl. work) ja yksikkö on joule ([[$J$]]).
Voiman tekemä työ siirrettäessä
Kun kappaletta siirretään pintaa pitkin, niin siirtämiseen vaadittavan voiman [[$F$]] määrää kappaleen ja pinnan välinen kitka. Mitä suurempi kitka kappaleen ja pinnan välillä on, niin sitä suurempi on tarvittava voima.
Kun kappaletta siirretään pintaa pitkin, niin tehty työ [[$W$]] lasketaan tarvittavan voiman [[$F$]] ja siirrettävän matkan [[$s$]] avulla kaavalla [[$$W=F \cdot s,$$]] missä voiman [[$F$]] yksikkö on newton ja matkan [[$s$]] yksikkö on metri.
| Esimerkki Stefan harrastuksena on autojen laittaminen. Stefa mittasi dynamometrissä auton tuottamaksi voimaksi kiihdytyksessä keskimäärin [[$4200 \ N$]]. Kiihdytysajoissa ajetaan 400 metrin matka koko ajan kiihdyttäen. Stefan auto tekee yhden kiihdytyksen aikana työtä [[$$ \begin{align} W&=F \cdot s \\ &=4200 \ N \cdot 400 \ m=1 \ 680 \ 000 \ J. \end{align} $$]] |
Nostossa tehty työ
Kun kappaletta nostetaan, niin nostamiseen vaadittavan voiman määrää kappaleen paino. Mitä enemmän kappale painaa, niin sitä enemmän on tehtävä työtä sen nostamiseksi.
Kun kappaletta nostetaan, niin tehty työ [[$W$]] lasketaan kappaleeseen kohdistuvan painovoiman [[$G=m \cdot g$]] ja nostokorkeuden [[$h$]] avulla kaavalla [[$$ \begin{align} W&=G \cdot h \\ &=m \cdot g \cdot h, \end{align} $$]] missä [[$m$]] on kappaleen massa kilogrammoina, [[$g \approx10 \frac{m}{s^2} $]] on putoamiskiihtyvyys ja [[$h$]] on nostokorkeus metreinä.
| Esimerkki Masan massa on [[$85 \ kg$]]. Noustessaan [[$3$]] metriä korkeat rappuset Masan tekemän nostotyön [[$W$]] määrä on [[$$ \begin{align} W&=m \cdot \ g \cdot h \\ &=85 \ kg \cdot 10 \frac{m}{s^2} \cdot 3 \ m=2 \ 550 \ J. \end{align} $$]] |
Teho
Kiihdytyskilpailuissa yleensä tehokkain auto voittaa, sillä mitä enemmän autossa on tehoa, niin sitä lyhyemmässä ajassa auto ajaa kiihdytysuoran alusta loppuun.
Tehokkaampi auto on todennäköisempi voittaja kiihdytysajoissa.Fysiikassa teho kuvaa työntekonopeutta. Mitä nopeammin jokin työ tehdään, niin sitä suurempi on teho.
Tehon tunnus on [[$P$]] (engl. power) ja yksikkö on watti ([[$W$]]).
(Etenkin moottoriajoneuvoissa tehon yksikkönä käytetään hevosvoimaa [[$hp$]] (engl. horsepower). Yksi hevosvoima on noin [[$736$]] wattia.)
Teho [[$P$]] lasketaan tehdyn työn [[$W$]] ja työhön käytetyn ajan [[$t$]] avulla kaavalla [[$$P=\frac{W}{t},$$]] missä ajan yksikkönä on sekunti.
| Esimerkki Yhden vesilitran lämmittämiseen kiehuvaksi tarvitaan [[$336 \ kJ=330 \ 600 \ J$]] energiaa. Vedenkeitin lämmittää litran vettä kiehuvaksi kahdessa minuutissa. Tällöin vedenkeittimen teho [[$P$]] on [[$$P=\frac {W}{t}=\frac{330 \ 600 \ J}{120 \ s}=2800 \ W.$$]] Eli vedenkeittimen teho on [[$2800$]] wattia. |
Hyötysuhde
Auton moottori tekee työtä muuttaessaan polttoaineen sisältämää kemiallista energiaa liike-energiaksi. Polttoaineen sisältämä energia ei kuitenkaan muutu kokonaan renkaiden liikkeeksi, vaan osa energiasta kuluu moottorin synnyttämään lämpöön ja ääneen. Myös hehkulampun kuluttamasta sähköenergiasta suuri osa menee "hukkaan" hehkulampun synnyttämän lämmön takia.
Laitteen hyötysuhde ilmoittaa kuinka monta prosenttia kone tuottaa hyödyllistä energiaa.
Esimerkiksi sähkövoimalan hyötysuhde voi olla [[$80 \%$]]. Tällöin voimalan polttoaineen sisältämästä energiasta [[$80 \%$]] saadaan muutettua sähköksi ja loput [[$20 \%$]] "menee harakoille".