1. Liike- ja potentiaalienergia
Liike- ja potentiaalienergia
Luvussa Lämpö, energia ja yhteiskunta kävimme läpi energian eri muotoja: lämpöä, sähköä, kemiallista energiaa ynnä muita energiamuotoja. Kävimme myös läpi sen, että energia voi muuttaa muotoaan, mutta energiaa ei koskaan häviä. Tässä kappaleessa keskitymme kahteen energiamuotoon: liike- ja potentiaalienergiaan.
Liike-energia
Mikään liikkeessä oleva kappale ei ole saavuttanut liiketilaansa "ilmaiseksi". Saadaksesi polkupyörän liikkeelle sinun on uhrattava kehosi kemiallista energiaa. Auton moottorissa polttoaineen kemiallinen energia muuttuu ensin lämmöksi, joka edelleen muuttuu liikkeeksi. Aseen luodin huima nopeus on seurausta laukaisussa tapahtuvan räjähdyksen vapauttamasta energiasta.
Kaikilla liikkeessä olevilla kappaleilla on liike-energiaa. Liike-energia on muodostunut tavalla tai toisella muista energiamuodoista. Kappaleen liike-energian suuruus riippuu kahdesta tekijästä: kappaleen massasta ja nopeudesta.
Mitä suurempi kappaleen massa on, niin sitä enemmän sillä on liike-energiaa liikkuessaan tietyllä nopeudella. Keilapallon heittäminen tekee paljon enemmän vahinkoa kuin tennispallo, sillä keilapallolla on massansa takia paljon liike-energiaa.
 Henkilöauton ja kuorma-auton törmäyksessä henkilöautolle käy huonosti, sillä kuorma-autolla on suuremman massansa takia enemmän liike-energiaa.
Henkilöauton ja kuorma-auton törmäyksessä henkilöautolle käy huonosti, sillä kuorma-autolla on suuremman massansa takia enemmän liike-energiaa.
Mitä nopeammin kappale liikkuu, niin sitä enemmän sillä on liike-energiaa. Aseen kevyt luoti ei tee vahinkoa heitettäessä, mutta kun luoti saa suuren nopeuden aseella ammuttaessa, niin sen vaikutukset ovat tuhoisat suuren liike-energian takia.
Liike-energiaa merkitään lyhyessä muodossa [[$E_k$]] (engl. kinetic energy) ja sen yksikkö on energian yksikkö joule ([[$J$]]).
Kappaleen, jonka massa on [[$m$]] ja nopeus on [[$v$]], liike-energia lasketaan kaavalla [[$$E_k=\frac{1}{2} \cdot m \cdot v^2,$$]] missä massan [[$m$]] yksikkö on kilogramma ja nopeuden [[$v$]] yksikkö on [[$\frac{m}{s}$]].
Potentiaalienergia
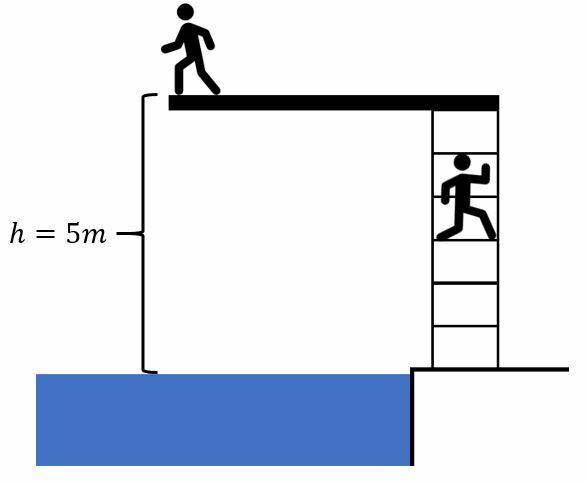
Jos hyppäät uimalassa hyppytornista, niin nopeutesi kasvaa suureksi ennen veteen osumista. Koska putoat kovaa vauhtia, niin sinulla on myös liike-energiaa. Mutta mistä kehosi on saanut vauhtiin tarvittavan liike-energian?
Kehosi on joutunut tekemään työtä painovoimaa vastaan kiivetessäsi hyppytorniin. Painovoimaa vastaan tehty työ "varastoituu" kehoosi potentiaalienergiaksi. Kun hyppäät tornista, niin potentiaalienergia muuttuu liike-energiaksi pudotessasi kohti vettä. Silmänräpäys ennen veteen osumista kaikki potentiaalienergia on muuttunut liike-energiaksi ja putoamisnopeus on suurimmillaan.
Kappaleen potentiaalienergia [[$E_P$]] riippuu sen massasta [[$m$]] ja korkeudesta [[$h$]] valittuun nollatasoon nähden. Potentiaalienergia lasketaan kaavalla [[$$E_p=m \cdot g \cdot h,$$]]missä [[$m$]] on massa, [[$h$]] on korkeus nollatasosta ja [[$g=10 \frac{m}{s^2}$]] on putoamiskiihtyvyys.
Mekaaninen energia
Mekaanisella energialla tarkoitetaan liike- ja potentiaalienergian summaa.
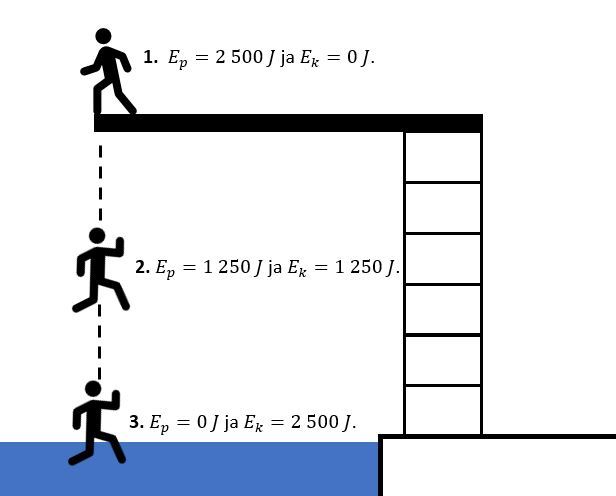
Edellisessä esimerkissä uimahyppääjän ollessa ylhäällä tornissa hänellä on vain potentiaalienergiaa eikä yhtään liike-energiaa (1).
Hyppääjän ollessa puolivälissä putoamistaan potentiaalienergiasta on jäljellä puolet alkuperäisestä, jolloin toinen puolisko on muuttunut liike-energiaksi (2).
Osuessaan veteen hyppääjällä ei ole enää potentiaalienergiaa, eli kaikki potentiaalienergia on muuttunut liike-energiaksi (3).
Hypyn jokaisessa vaiheessa hyppääjän potentiaali- ja liike-energian summa, eli mekaaninen energia, on [[$2 \ 500 \ J$]] eli [[$E_p+E_k=2 \ 500 \ J$]].
Liike-energia
Mikään liikkeessä oleva kappale ei ole saavuttanut liiketilaansa "ilmaiseksi". Saadaksesi polkupyörän liikkeelle sinun on uhrattava kehosi kemiallista energiaa. Auton moottorissa polttoaineen kemiallinen energia muuttuu ensin lämmöksi, joka edelleen muuttuu liikkeeksi. Aseen luodin huima nopeus on seurausta laukaisussa tapahtuvan räjähdyksen vapauttamasta energiasta.
Kaikilla liikkeessä olevilla kappaleilla on liike-energiaa. Liike-energia on muodostunut tavalla tai toisella muista energiamuodoista. Kappaleen liike-energian suuruus riippuu kahdesta tekijästä: kappaleen massasta ja nopeudesta.
Mitä suurempi kappaleen massa on, niin sitä enemmän sillä on liike-energiaa liikkuessaan tietyllä nopeudella. Keilapallon heittäminen tekee paljon enemmän vahinkoa kuin tennispallo, sillä keilapallolla on massansa takia paljon liike-energiaa.
 Henkilöauton ja kuorma-auton törmäyksessä henkilöautolle käy huonosti, sillä kuorma-autolla on suuremman massansa takia enemmän liike-energiaa.
Henkilöauton ja kuorma-auton törmäyksessä henkilöautolle käy huonosti, sillä kuorma-autolla on suuremman massansa takia enemmän liike-energiaa.Mitä nopeammin kappale liikkuu, niin sitä enemmän sillä on liike-energiaa. Aseen kevyt luoti ei tee vahinkoa heitettäessä, mutta kun luoti saa suuren nopeuden aseella ammuttaessa, niin sen vaikutukset ovat tuhoisat suuren liike-energian takia.
Liike-energiaa merkitään lyhyessä muodossa [[$E_k$]] (engl. kinetic energy) ja sen yksikkö on energian yksikkö joule ([[$J$]]).
Kappaleen, jonka massa on [[$m$]] ja nopeus on [[$v$]], liike-energia lasketaan kaavalla [[$$E_k=\frac{1}{2} \cdot m \cdot v^2,$$]] missä massan [[$m$]] yksikkö on kilogramma ja nopeuden [[$v$]] yksikkö on [[$\frac{m}{s}$]].
| Esimerkki Rynnäkkökiväärin luodin nopeus on [[$715 \frac{m}{s}$]] ja luodin massa on [[$8$]] grammaa. Tällöin luodin liike-energia [[$E_k$]] on [[$$ \begin{align} E_k &=\frac{1}{2} \cdot m \cdot v^2 \\ &=\frac{1}{2} \cdot 0,008kg \cdot (715\frac{m}{s})^2\approx2040 \ J. \end{align}$$]] Vertailun vuoksi keilaradalla vierivän keilapallon, jonka massa on [[$5 \ kg$]] ja nopeus [[$5 \frac{m}{s}=18 \frac{km}{h}$]], liike-energia [[$E_k$]] on [[$$E_k=\frac{1}{2} \cdot 5kg \cdot (5 \frac{m}{s})^2 \approx 63 \ J.$$]] Luodin liike-energia on siis yli 30-kertainen keilapalloon verrattuna! |
Potentiaalienergia
Jos hyppäät uimalassa hyppytornista, niin nopeutesi kasvaa suureksi ennen veteen osumista. Koska putoat kovaa vauhtia, niin sinulla on myös liike-energiaa. Mutta mistä kehosi on saanut vauhtiin tarvittavan liike-energian?
Kehosi on joutunut tekemään työtä painovoimaa vastaan kiivetessäsi hyppytorniin. Painovoimaa vastaan tehty työ "varastoituu" kehoosi potentiaalienergiaksi. Kun hyppäät tornista, niin potentiaalienergia muuttuu liike-energiaksi pudotessasi kohti vettä. Silmänräpäys ennen veteen osumista kaikki potentiaalienergia on muuttunut liike-energiaksi ja putoamisnopeus on suurimmillaan.
Kappaleen potentiaalienergia [[$E_P$]] riippuu sen massasta [[$m$]] ja korkeudesta [[$h$]] valittuun nollatasoon nähden. Potentiaalienergia lasketaan kaavalla [[$$E_p=m \cdot g \cdot h,$$]]missä [[$m$]] on massa, [[$h$]] on korkeus nollatasosta ja [[$g=10 \frac{m}{s^2}$]] on putoamiskiihtyvyys.
Mekaaninen energia
Mekaanisella energialla tarkoitetaan liike- ja potentiaalienergian summaa.
Edellisessä esimerkissä uimahyppääjän ollessa ylhäällä tornissa hänellä on vain potentiaalienergiaa eikä yhtään liike-energiaa (1).
Hyppääjän ollessa puolivälissä putoamistaan potentiaalienergiasta on jäljellä puolet alkuperäisestä, jolloin toinen puolisko on muuttunut liike-energiaksi (2).
Osuessaan veteen hyppääjällä ei ole enää potentiaalienergiaa, eli kaikki potentiaalienergia on muuttunut liike-energiaksi (3).
Hypyn jokaisessa vaiheessa hyppääjän potentiaali- ja liike-energian summa, eli mekaaninen energia, on [[$2 \ 500 \ J$]] eli [[$E_p+E_k=2 \ 500 \ J$]].