8.2 Radioaktiivisuus ja ydinreaktiot

Radioaktiivisuus

Monet isotoopit ovat radioaktiivisia eli hajoavat spontaanisti. Tavanomaiset hajoamisen tavat ovat alfa- ja beetahajoaminen sekä elektronisieppaus. Isotooppitaulukkoon on kirjattu eri isotooppien tyypillinen hajoamistapa, puoliintumisaika ja massa. Pysyvien isotooppien kohdalla on ilmaistu niiden prosenttiosuus luonnossa. Esimerkiksi berylliumin isotoopit ovat seuraavanlaiset.

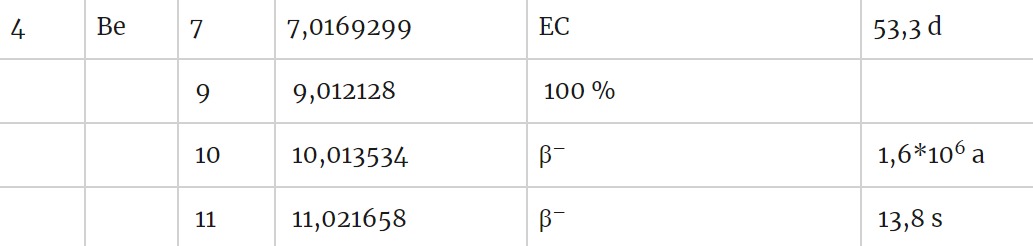
Alfahajoamisessa radioaktiivisen isotoopin ytimestä irtoaa alfahiukkanen eli heliumydin. Esimerkiksi:

[[$ \quad ^{211}_{83}\text{Bi} \rightarrow ^{207}_{81}\text{Au}+^4_2\text{He} $]]

Beeta^--hajoamisessa ytimen neutroni muuttuu protoniksi, elektroniksi ja antineutriinoksi. Kokonaissähkövaraus ja massaluku säilyvät. Esimerkiksi:

[[$ \quad ^{95}_{40}\text{Zr} \rightarrow ^{95}_{41}\text{Nb}+^0_{-1}\text{e}+\bar{v} $]]

Beeta⁺-hajoamisessa ytimen protoni muuttuu neutroniksi, positroniksi ja neutriinoksi. Kokonaissähkövaraus ja massaluku säilyvät. Esimerkiksi:

[[$ \quad ^{78}_{35}\text{Br} \rightarrow ^{78}_{34}\text{Se}+^0_{+1}\text{e}+v $]]

Elektronisieppauksessa ydin kaappaa elektronin omalta elektronikuoreltaan, jolloin sen protoni muuttuu neutroniksi ja neutriinoksi. Esimerkiksi:

[[$ \quad \text{e}+^{49}_{23}\text{V} \rightarrow ^{49}_{22}\text{Ti}+v $]]

Gammasäteilyä lähettävä ydin ei muutu toiseksi vaan kyse on ytimen viritystilan purkautuessa vapautuvasta energiasta. Usein radioaktiivisen hajoamisreaktion tytärydin jää viritystilaan, joka purkautuu myöhemmin. Gammasäteilyä havaitaan siis usein esim alfa- hajoamisen yhteydessä.

Aktiivisuus ja hajoamislaki

Näytteen aktiivisuus kertoo, kuinka monta hajoamista siinä tapahtuu sekunnissa. Aktiivisuuden yksikkö on becquerel, Bq (sama kuin 1/s). Aktiivisuus liittyy hajoamisvakion kautta radioaktiivisten ydinten määrään: [[$A=\lambda N$]]

Radioaktiivisesta näytteestä hajoaa tietyssä ajassa aina yhtä suuri prosenttiosuus.

Näytteessä jäljellä olevien radioaktiivisten ydinten määrä noudattaa mallia [[$N(t)=N_0e^{-\lambda t}$]], missä [[$\lambda$]] on hajoamisvakio. Mitä suurempi hajoamisvakio, sitä nopeammin näyte hajoaa.

Hajoamisvakion sijaan hajoamisnopeutta kuvataan usein puoliintumisajalla [[$T_{1/2}$]], joka kertoo, missä ajassa puolet radioaktiivisista ytimistä hajoaa. Puoliintumisaika liittyy hajoamisvakioon: [[$T_{1/2}=\dfrac{\ln 2}{\lambda}$]].

Radioaktiivisen hajoamisen ja muiden ydinreaktioiden energia

Ydinreaktiossa joko vapautuu energiaa tai siinä sitoutuu energiaa. Tulos riippuu siitä, kummassa tilanteessa nukleonit ovat tiiviimmin sitoutuneet toisiinsa: lähtöytimissä vai syntyvissä ytimissä. Radioaktiivisessa hajoamisessa vapautuu aina energiaa, sillä se tapahtuu spontaanisti.

Reaktion energia saadaan laskemalla "lopputuotteiden massat" - "alkutuotteiden massat" ja muuttamalla tämä massa energiaksi vastaavuuden [[$E=mc^2$]] mukaisesti.

Ydinreaktioihin osallistuvien ytimien massat saadaan vähentämällä isotooppitaulukon atomimassoista atomiin kuuluvien elektronien kokonaismassa.
Massan muutos on järkevää laskea välituloksena yksikössä u.
Energian laskemisessa voidaan hyödyntää yhtä atomimassayksikköä vastaavaa tunnettua energiamäärää: [[$ \mathrm{u}=931{,}49\ \dfrac{\mathrm{MeV}}{c^2} $]]

Esimerkki: Beetahajoamisen energia

Tarkastellaan hajoamisen laskennallista käsittelyä isotoopille Mg-23. Kyseessä on beeta+-aktiivinen isotooppi, jonka hajoamisen reaktioyhtälö on seuraava:

[[$\quad ^{23}_{12}\text{Mg} \rightarrow {^{23}_{11}\text{Na}}+{^{\ \ \ 0}_{+1}\text{e}}^++\nu $]]

Massan muutoksen laskemiseksi etsitään atomien massat isotoopppitaulukosta. Ydinten massat saadaan vähentämällä niistä atomin elektronien kokonaismassa:

[[$ \quad \begin{align}m_{\text{Mg-ydin}}&=m_{\text{Mg-atomi}}-12 m_\text{e} \\ \, \\ m_{\text{Na-ydin}}&=m_{\text{Na-atomi}}-11m_\text{e} \\ \end{align} $]]

Massan muutos saadaan vähentämällä emoytimen eli magnesiumin massasta reaktiossa syntyvien natriumytimen ja positronin massat. Positronin massa on sama kuin elektronin.

[[$ \quad \begin{align} \Delta m &=m_{\text{Mg-ydin}}-m_{\text{Na-ydin}}-m_{\text{positroni}} \\ \, \\ &=m_{\text{Mg-atomi}}-12 m_\text{e}-(m_{\text{Na-atomi}}-11m_\text{e})-m_\text{e} \quad \\ \, \\ &=m_{\text{Mg-atomi}}-m_{\text{Na-atomi}}-2m_\text{e} \\ \, \\ &= 22,994124 \text{ u}-22,989767 \text{ u}-2\cdot 5,485799\cdot 10^{-4} \text{ u} \\ \, \\ &=0,0032598402 \text{ u}\approx 0,003260 \text{ u} \\ \end{align} $]]

Massan muutos on 0,003260 u. Huomataan, että vähennyslaskun vastaus saadaan neljän merkitsevän numeron tarkkuudella. Reaktioenergia on siis

[[$ \quad Q=\Delta m c^2=0,0032598402 \cdot 931,49 \text{ MeV/c}^2\cdot c^2 \approx 3,037 \text{ MeV} $]]