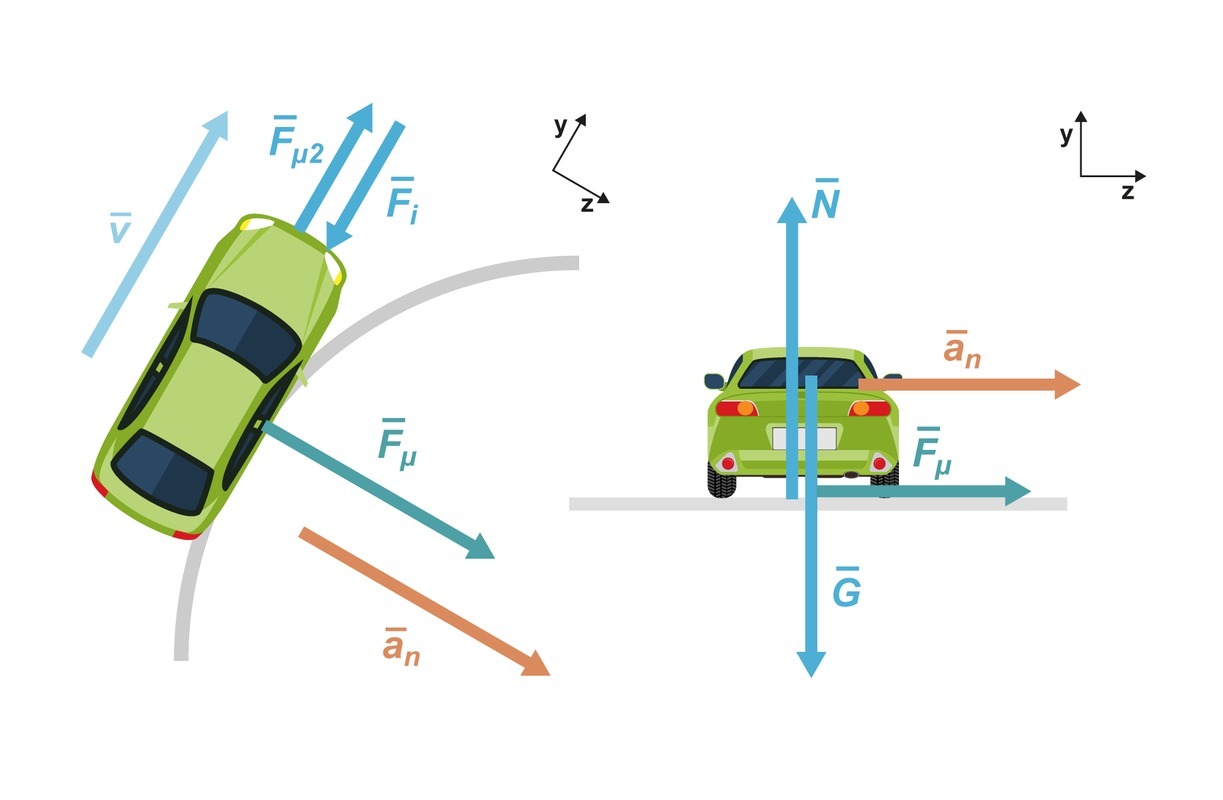
Auto ympyräradalla
Auto ajaa vaakasuoralla tiellä ympyränmuotoisessa kaarteessa, jonka ratasäde on 55 m. Auton nopeus on 78 km/h. Kuinka suuri kitkakerroin renkaiden ja tien välillä tulee olla, jotta auto pysyy radallaan?
RatkaisuMääritetään aluksi autoon vaikuttavat voimat. Piirretään tilanteesta voimakuvio. Koska nopeus ei muutu, pysyy voimakuvio samanlaisena koko liikkeen ajan.
Vasen voimakuvio on piirretty ylhäältä ja oikea takaa siten, että ympyräradan keskipiste on oikealla. [[$G$]] on auton paino, ja [[$N$]] tienpinnan tukivoima. Jos oletetaan liikettä vastustavien voimien [[$F_\text{i}$]] olevan vähäisiä, liikkeen suunnassa ([[$x$]]-suunta) ei ole lainkaan voimia (koska ratanopeus on vakio) ja kitkavoima [[$F_\mu$]] suuntautuu pelkästään kohti ympyräradan keskipistettä pitäen auton ympyräradalla. Ympyrärataehdon mukaan normaalikiihtyvyys [[$a_n=\dfrac{v^2}{r}$]], mikä on [[$z$]]-suunnan kiihtyvyys. Auto ei liiku pystysuunnassa, joten y-suunnassa kiihtyvyys on nolla. Dynamiikan peruslain mukaan [[$\Sigma \bar{F}=m\bar{a}$]]. Kirjoitetaan liikeyhtälöt [[$z$]]- ja [[$y$]]-suunnassa:
[[$\quad \begin{cases} F_\mu=ma_n \\ N-G=0 \\ \end{cases}$]]
[[$\quad \begin{cases} N\mu=m\dfrac{v^2}{r} \\ N-mg=0 \\ \end{cases}$]]
Alemmasta yhtälöstä saadaan [[$N=mg$]]. Sijoitetaan tämä ylempään yhtälöön, ja ratkaistaan kitkakerroin. Tulokseksi saadaan:
[[$ \begin{align*} \quad mg\mu&=m\dfrac{v^2}{r} \\ \, \\ \mu & =\dfrac{v^2}{gr} \\ \, \\ & =\dfrac{\left(\dfrac{78}{\text{3,6}}\text{ m/s}\right)^2}{\text{9,81 m/s}^2\cdot 55\text{ m}} \\ \, \\ &=\text{0,870}\dotso\approx \text{0,87} \\ \end{align*} $]]
Kitkakertoimen on oltava vähintään 0,87. Tämä on varsin suuri kitkakerroin. Kun otetaan huomioon kaarteen jyrkkyys, auto ajaa vaarallisen suurella nopeudella.