2.3 Graafisia tehtäviä

Graafisia perustehtäviä

Tehtävät 1-30 sisältävät erityyppisiä graafisia tehtäviä monista eri aiheista.
Tehtävät 31-40 ovat haastavampia graafisia tehtäviä. Nämä ovat laajempia tehtäviä tai edellyttävät vaativampaa teoreettista käsittelyä.

1. YO s2011

Luiden kimmoisuus vähenee ihmisen ikääntyessä. Luun kimmoisuutta voidaan tutkia kuormittamalla luuta erilaisilla voimilla ja mittaamalla luun venymä tai taipuma. Kohtuullisilla kuormituksilla luu noudattaa Hooken lakia σ = Eε , jossa σ on jännitys, E on luun kimmokerroin ja ε on suhteellinen venymä. Oheisessa taulukossa on eräässä kokeessa mitatut reisiluun suhteelliset venymät ja vastaavat jännitykset.
 

σ (MN/m2)

0,0

5,00

10,0

15,0

20,0

25,0

30,0

35,0

ε

0,0

0,00031

0,00063

0,00094

0,0013

0,0016

0,0019

0,0022

 a) Piirrä jännitys suhteellisen venymän funktiona.
b) Määritä kuvaajan avulla reisiluun kimmokerroin.

1.

  • Palauta vastaus

Sinulla ei ole tarvittavia oikeuksia lähettää mitään.

1.

  • Palauta kuva tai muu tiedosto
  • Palauta merkintä
  • Palauta linkki

Sinulla ei ole tarvittavia oikeuksia lähettää mitään.

2. YO k2012 #2

Kumilankaa venytetään erisuuruisilla voimilla ja mitataan langan pituus. Voimat ja niitä vastaavat pituudet on esitetty oheisessa taulukossa ja tiedostossa:YO k2012 #2.cmbl

Voima (N)

0,5

1,0

2,0

3,0

4,0

5,0

6,0

8,0

10,0

12,0

x (mm)

92

105

143

190

241

284

321

367

395

416

a) Piirrä F(x).
b) Määritä kuvaajan perusteella kumilangan pituus, kun sitä venytetään 7,0 N voimalla.
c) Arvioi kuvaajan perusteella kumilangan pituus, kun sitä ei venytetä.

2.

  • Palauta vastaus

Sinulla ei ole tarvittavia oikeuksia lähettää mitään.

3. YO s2012

Fysiikan työkurssilla annettiin tehtäväksi mitata putoamiskiihtyvyys. Lukiolainen kuvasi videokameralla putoavaa palloa, määritti videolta pallon nopeuksia ja kirjasi ne oheisen taulukon mukaisesti. Määritä tuloksista graafisesti pallon putoamiskiihtyvyys.

t (s)

1,48

1,52

1,56

1,60

1,64

1,68

1,72

1,76

v (m/s)

0,22

0,64

1,04

1,40

1,79

1,57

2,57

2,95

3.

  • Palauta vastaus

Sinulla ei ole tarvittavia oikeuksia lähettää mitään.

4. YO s2017

Liikennevaloista suoraan eteenpäin lähtevän auton nopeus mitattiin ajan funktiona. Mitatut
arvot on annettu oheisessa taulukossa ja tiedostossa.
YOs2017.cmbl

t (s) 0,0 1,0 2,0 3,0 4,0 6,0 8,0 10,0 12,0 14,0
v (m/s) 0,0 0,1 0,5 2,0 4,0 8,5 12,5 15,0 16,0 16,0

a) Piirrä kuvaaja auton nopeudesta v ajan t funktiona. (3 p.)
b) Määritä auton kulkema matka aikavälillä 0,0...14,0 s. (2 p.)
c) Määritä auton keskinopeus aikavälillä 0,0...14,0 s. (1 p.)

4

  • Palauta vastaus

Sinulla ei ole tarvittavia oikeuksia lähettää mitään.

5. YO s2013

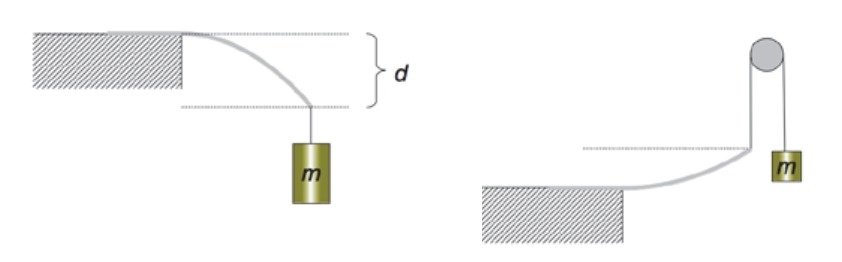Pöydän reunaan kuvan mukaisesti kiinnitettyä kevyttä, symmetristä viivoitinta kuormitetaan sen päästä eri massaisilla punnuksilla. Viivoittimen taipuma d eri punnuksen massoilla on esitetty taulukossa.

m (g)

0

25

50

75

100

150

200

300

400

500

d (cm)

0

1,1

2,1

3,1

4,0

5,9

7,5

10,1

12,1

13,5

a) Piirrä kuvaaja, joka esittää taipumaa kuormittavan voiman funktiona. (3 p.)

b) Kuinka paljon viivoitin taipuu, kun sitä kuormitetaan 350 g:n punnuksella? (1 p.)

c) Samaa viivoitinta taivutetaan ylöspäin langan, kitkattoman väkipyörän ja 65 g:n punnuksen avulla kuvan mukaisesti. Täydennä kohdan a kuvaaja niin, että se sisältää tätä tilannetta kuvaavan pisteen. (2 p.)

5.

  • Palauta kuva tai muu tiedosto
  • Palauta merkintä
  • Palauta linkki

Sinulla ei ole tarvittavia oikeuksia lähettää mitään.

6. YO k1997

Pistemäisestä lähteestä tulevan gammasäteilyn voimakkuutta mitattiin geigerputkella. Kun putken etäisyyttä säteilylähteestä muutettiin, laskentataajuus I pieneni oheisen taulukon mukaisesti:

YO k1997 graafinen.csv​ YO k1997 graafinen.cmbl

a) Piirrä I (r) -kuvaaja.
b) Määritä laskentataajuus, kun etäisyys on 7,0 cm.
c) Millainen matemaattinen riippuvuus näyttää vallitsevan säteilyn voimakkuuden ja etäisyyden välillä?
d) Selitä, miksi laskentataajuus pienenee em. tavalla, vaikka ilma ei juurikaan absorboi gammasäteilyä.

6.

  • Palauta kuva tai muu tiedosto
  • Palauta merkintä
  • Palauta linkki

Sinulla ei ole tarvittavia oikeuksia lähettää mitään.

7. Tehtävä laajalla data-aineistolla

Kingi on Linnanmäen huvipuiston suosittu laite, jonka kyydissä matkustajat hinataan kymmenien metrien korkeuteen, jonka jälkeen he putoavat miltei vapaasti lähelle lähtökorkeutta. Koehenkilö mittasi älypuhelimella kiihtyvyyttään Kingin noustua ylös. Positiivinen suunta oli valittu ylöspäin. Tulokset ovat tiedostossa.
Lisätehtävä laajalla aineistolla FY9.csv​

a) Esitä tulokset aika–kiihtyvyys-koordinaatistossa.

b) Mikä on suurin kiihtyvyyden arvo? Selitä, missä liikkeen vaiheessa tämä saavutetaan.

c) Määritä kuvaajan perusteella matkustajan maksimivauhti.

:left:right

7.

  • Palauta kuva tai muu tiedosto
  • Palauta merkintä
  • Palauta linkki

Sinulla ei ole tarvittavia oikeuksia lähettää mitään.

8. YO k2005

Härkäsammakoille (Rana catesbeiana) pidetään hyppykilpailuja, joissa parhaat yksilöt hyppäävät yli kaksi metriä pitkiä loikkia. Biologit videoivat tuhansia kilpailuhyppyjä. Taulukko esittää erään härkäsammakon ratanopeuden sammakon ponnistaessa.
 

t (s)

0,00

0,04

0,08

0,12

0,16

0,20

0,24

0,28

0,32

0,36

0,40

v (m/s)

0,00

0,31

1,02

1,99

2,85

3,57

4,22

4,56

4,57

4,35

3,86

a) Piirrä sammakon ratanopeuden kuvaaja ajan funktiona. (3 p.)
b) Merkitse ratanopeuden kuvaajalle piste, jossa sammakon ratanopeus on suurin. (1 p.)
c) Määritä ratanopeuden kuvaajasta sammakon kiihtyvyys hetkellä 0,24 s. (2 p.)

8.

  • Palauta kuva tai muu tiedosto
  • Palauta merkintä
  • Palauta linkki

Sinulla ei ole tarvittavia oikeuksia lähettää mitään.

9. YOs2018 #2 kahvin jäähtyminen

Pekka tutki kahvin jäähtymistä emalimukissa. Hän kaatoi kahvia mukiin, mittasi kahvin lämpötilan minuutin välein ja kirjasi tulokset tietokoneelle. Pekan mittaussarjan tulokset on annettu oheisessa taulukossa.

kahvi.cmbl

2.1 Laadi valitsemallasi ohjelmalla mittaussarjan tuloksista kahvin lämpötilan kuvaaja ajan funktiona ja liitä kuvaaja kuvakaappauksena vastauslaatikkoon. (5 p.)

2.2 Kahvia oli mukissa 192 ml. Kuinka paljon lämpöä kahvi luovutti ympäristöön aikavälillä 2,5 min – 5,5 min? (5 p.)

2.3 Kahvia oli mukissa 192 ml. Kuinka suurella teholla kahvia pitäisi lämmittää mukissa, että kahvin lämpötila pysyisi 65 °C:ssa? (5 p.)

9.

  • Palauta vastaus

Sinulla ei ole tarvittavia oikeuksia lähettää mitään.

10. Sovitettavan käyrän parametrien hyödyntäminen

Radioaktiivista näytettä havainnoitiin säteilymittarilla. Mittarin sekunnin kuluessa mittaama säteily muuttui 8 tunnin aikana oheisen taulukon mukaisesti. ​Mitatu säteily.csv​

Määritä mittausdatan perusteella tutkitun isotoopin puoliintumisaika.

10.

  • Palauta vastaus

Sinulla ei ole tarvittavia oikeuksia lähettää mitään.

11. Tehtävä sovituksen parametreista ja lasketun sarakkeen käytöstä

Puhallinmoottorilla varustettu vaunu eteni vaunuradan päästä päähän. Mittauksen alussa ja lopussa vaunu oli levossa. 
Vaunun paikan mittaus.cmbl

a) Sovita mittauspisteisiin sopiva käyrä ja osoita, että vaunun nopeus kasvoi tasaisesti sen liikkuessa. 
b) Esitä vaunun nopeus ja kiihtyvyys erillisinä kuvaajina.

11.

  • Palauta kuva tai muu tiedosto
  • Palauta merkintä
  • Palauta linkki

Sinulla ei ole tarvittavia oikeuksia lähettää mitään.

12. Tehtävä idealisoidusta kuvaajasta

Herkkäliikkeinen vaunu liikkui vaunuradalla. Sen nopeutta mitattiin optisella anturilla. Tulokset ovat alla erillisenä tiedostona. 

a) Hahmottele vaunun kiihtyvyyden periaatekuvaaja. (Huom. piirrä murtoviiva, jossa erottuvat olennaisimmat kohdat ja kiihtyvyyden muutokset. Voit piirtää kuvaajan esim. Loggerprolla muutamia yksittäisiä pisteitä yhdistävänä murtoviivana)

b) Esitä tarkka mittauspisteiden perusteella määritetty kiihtyvyyden kuvaaja. (Määritä esim. Loggerpro:lla sopivasti määritellyn lasketun sarakkeen avulla.)

Vaunun nopeus.cmbl

12.

  • Palauta vastaus

Sinulla ei ole tarvittavia oikeuksia lähettää mitään.

31. YO s2019 #11

Maanjäristykset aiheuttavat korkeissa rakennuksissa värähtelyjä, jotka saattavat olla tuhoisia. Värähtelyjä voidaan tutkia pienoismallien ja kiihtyvyysantureiden avulla. Videossa 11.A on esitetty korkean rakennuksen puinen pienoismalli, joka saatetaan värähtelemään. Havaitaan, että värähtely vaimenee. Pienoismallin yläpinnan kiihtyvyys on mitattu ajan funktiona, ja mittaustulokset ovat tiedostossa 11.B.

Yksinkertaisin matemaattinen malli värähtelijän kiihtyvyydelle vaimenevassa värähtelyssä on [[$ a\left(t\right)=Ae^{^{-Bt}}\cos\left(Ct\right) $]]​, jossa A, B ja C ovat parametreja. Parametri A on värähtelyn amplitudi hetkellä t. Parametri [[$ B=\frac {\ln 2}{T_{1/2}} $]]​, jossa [[$ T_{1/2} $]]​ on aika, jossa värähtelyn amplitudi pienenee puoleen. Parametri [[$ C=2\pi f $]]​, jossa f on värähtelyn taajuus. Mallissa funktio [[$ a\left(t\right)=Ae^{^{-Bt}} $]]​on värähtelyn eksponentiaalisesti vaimeneva amplitudi ja funktio [[$ \cos\left(Ct\right) $]]​ kuvaa puolestaan värähtelyn periodista vaihtelua.

Aineisto: 11.A Video: rakennuksen pienoismalli 11.B Mittaustulokset T11_B.cmbl

11.1
Kuinka suuri on pienoismallin värähtelyn taajuus? (5 p.)
 
11.2
Yksi maanjäristyksen riskeistä on, että esineet rakennusten sisällä eivät pysy paikoillaan, vaan alkavat liukua ja aiheuttavat tuhoa. Tämän tutkimiseksi pienoismallin päälle asetetaan pieni laakea kivi, jonka massa on 21 g. Pysyykö kivi liukumatta paikallaan värähtelyn ajan? Oletetaan, että pienoismalli värähtelee samalla tavalla kuin ilman kiveä. (10 p.)
 
11.3
Missä ajassa värähtelijän kiihtyvyyden kunkin värähdyksen aikana saavuttama suurin arvo pienenee kahdeksasosaan? (5 p.)

31.

  • Palauta kuva tai muu tiedosto
  • Palauta merkintä
  • Palauta linkki

Sinulla ei ole tarvittavia oikeuksia lähettää mitään.

32. YO k200X

Kalorimetrissä, jonka lämpökapasiteetti on 120 J/ᵒC, on 150 g punaista pakkasnestettä. Nestettä lämmitetään uppokuumentimella 15,2 W:n vakioteholla, jolloin nesteen lämpötila muuttuu ajan funktiona oheisen taulukon mukaisesti.

Määritä taulukon perusteella piirrettyä kuvaajaa hyväksi käyttäen pakkasnesteen ominaislämpökapasiteetti.

t (min) 0 2,0 4,0 6,0 8,0 10,0 12,0 14,0 16,0
T ([[$ ^{\circ}C $]]​ 21,8 25,8 30,1 34,2 38,1 42,0 45,6 49,8 53,6



32

.
  • Palauta vastaus

Sinulla ei ole tarvittavia oikeuksia lähettää mitään.

33. YO2013 tehtävä 10

Pikajuoksua lyhyillä matkoilla voidaan kuvata niin, että aluksi juoksija kiihdyttää tasaisesti huippunopeuteen vmax, jolla hän sitten juoksee maaliin saakka. Oletetaan, että kiihtyvyys on aina sama maksimikiihtyvyys amax ja että kiihdytysaika t1 on sama kaikilla juoksumatkoilla. Kokonaisaika t2 on on kiihdytysajan ja huippunopeudella vmax juostun ajan summa.

a) Hahmottele kuvaaja, josta ilmenee juoksijan nopeus ajan funktiona. (2 p.)
b) Oheisessa taulukossa on esitetty suoralla radalla saavutettavia huippuaikoja. Esitä graafisesti matka ajan funktiona ja määritä amax, vmax ja t1. (4 p.)

Matka 50 yd 50 m 60 m 100 yd 100 m
Aika (s) 5,22 5,33 6,38 9,00 9,58

33.

  • Palauta kuva tai muu tiedosto
  • Palauta merkintä
  • Palauta linkki

Sinulla ei ole tarvittavia oikeuksia lähettää mitään.

34. YO k2012 (tehtävä 10)

Testattaessa erään auton suurinta kiihtyvyyttä saatiin oheinen nopeuden kuvaaja.

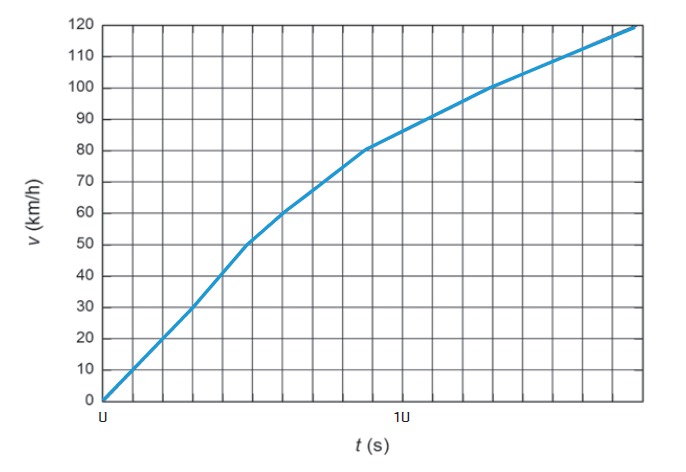
a) Määritä tarkoituksenmukaista kuvaajaa käyttäen teho, jolla auton liike-energia kasvaa välillä 30 km/h – 120 km/h. Auton massa on 1 420 kg. (4 p.)

b) Auton moottorin suurimmaksi tehoksi on ilmoitettu 77 kW. Mistä mahdollinen ero a-kohdan tulokseen voi johtua? (2 p.)

34.

  • Palauta kuva tai muu tiedosto
  • Palauta merkintä
  • Palauta linkki

Sinulla ei ole tarvittavia oikeuksia lähettää mitään.

35. YO k2018 jokeritehtävä +13

Veden pinta-aaltojen nopeuden riippuvuutta veden syvyydestä tutkittiin aaltoammekokeessa, jossa veden syvyyttä voitiin muuttaa. Vesiaallot synnytettiin värähtelijällä, jonka taajuus oli 10,0 Hz. Aallonpituuden λ mittaustulokset eri veden syvyyksillä h on annettu taulukossa.

h (mm)  3,0 3,5 4,0 4,5 5,0 5,3 6,3  
λ (mm) 13,9 14,5 16,0 16,8 17,7 18,3 19,6  


a) Selvitä, mikä seuraavista malleista i–iii kuvaa aaltojen nopeuden riippuvuutta veden sy-
vyydestä kaikkein parhaiten:

i) [[$ v=kh $]]​
ii) [[$ v=kh^2 $]]​
iii) ​[[$ v=k\sqrt h $]]​

Perustele vastauksesi graafisesti mittaustulosten avulla. (4 p.)

b) Määritä valitsemassasi mallissa esiintyvä verrannollisuuskerroin k yksikköineen. (2 p.)

c) Aaltoammeen pohjalle asetetaan koroke, joka on esitetty keltaisella kuvassa ylhäältä
päin. Ennen koroketta veden syvyys on 6,0 mm, ja korokkeen kohdalla 3,2 mm. Aaltorin-
tamat saapuvat jyrkkäreunaisen korokkeen muodostamaan rajapintaan vinosti kuvan
mukaisesti 63°:n tulokulmassa. Määritä aaltorintamien etenemissuunta korokkeen pääl-
lä. Kopioi kuva vastauspaperiisi, ja täydennä siihen tilanne, jossa aaltorintamat osuvat ra-
japintaan ja ylittävät sen. Kuvassa pitää näkyä aaltorintamat ja niiden etenemissuunta
ennen koroketta ja korokkeen päällä. (3 p.)

35.

  • Palauta kuva tai muu tiedosto
  • Palauta merkintä
  • Palauta linkki

Sinulla ei ole tarvittavia oikeuksia lähettää mitään.