3.1 Vetyatomin energiatasot ja säteily

Elektronin energiatilat vetyatomissa

Vetyatomin ydin on positiivisesti varautunut protoni. Se ja negatiivisesti varautunut elektroni vetävät toisiaan puoleensa, mikä selittää elektronin pysymisen protonin lähellä. Havaintojen mukaan vetyatomi on paljon suurempi kuin pelkkä protoni, eli jostain syystä elektroni ei vetovoimasta huolimatta liiku aivan kiinni protoniin. Ennen kvanttimekaniikkaa tämä selitettiin mallilla, jossa elektroni kiersi protonia samaan tapaan kuin planeetat kiertävät Aurinkoa. Mallin ongelma oli, että ympyrärataliikkeessä olevan elektronin pitäisi sähkömagnetismin teorian mukaan säteillä sähkömagneettista säteilyä, menettää energiaa ja pudota kiinni protoniin.

Kvanttimekaanisessa mallissa elektronilla ei ole täsmällistä paikkaa, vaan elektronin sijainnin todennäköisyysjakauma ratkaistaan Schrödingerin yhtälöstä. Todennäköisyysjakauma protonin ympärillä voi saada erilaisia pysyviä muotoja, joita kutsutaan orbitaaleiksi. Ei voida kuitenkaan sanoa, että elektroni liikkuisi orbitaalilla, tai että se ylipäänsä olisi jossain tietyssä pisteessä. Täten kysymys siitä, miksi elektroni ei putoa kohti ydintä, ei ole mielekäs kvanttimekaanisessa mallissa. Oikealla on eri orbitaalien muotoja. Elektroni sijaitsee todennäköisimmin valkoisilla ja epätodennäköisimmin violeteilla alueilla. Kuvat ovat poikkileikkauksia kolmiulotteisista orbitaaleista. Vety-ydin (protoni) on kuvissa keskellä.

Kuva oikealla: Elektronin sijainnin todennäköisyysjakaumia eri energiatiloilla ja vedyn aaltofunktio. Wikimedia Commons

Jokaista elektronin mahdollista tilaa, orbitaalia, vastaa tietty energia. Nämä energiat ovat Schrödingerin yhtälön ratkaisuja samaan tapaan kuin edellisessä aliluvussa laatikossa olevan elektronin energiat. Lukiotason ylittävän laskun lopputuloksena saadaan elektronin energiatiloiksi vetyatomissa seuraava kaava:

Elektronin energiatilat vetyatomissa

[[$ \quad E_n=-\dfrac{1}{n^2}\dfrac{m_\text{e}e^4}{8\epsilon_0^2h^2}\approx-\dfrac{1}{n^2}\cdot 13,6\text{ eV}$]]

Tässä [[$m_\text{e}$]] on elektronin massa, ja [[$e$]] on sen varaus, [[$\epsilon_0$]] on tyhjiön permittiivisyys ja [[$h$]] on Planckin vakio. [[$n$]] on jokin positiivinen kokonaisluku.

Laskujen kannalta on yleensä riittävää käyttää likiarvoa 13,6 eV luonnonvakioiden yhdistelmälle.

Tilassa [[$n=1$]] elektronin energia on -13,6 eV. Tätä kutsutaan elektronin perustilaksi, koska sen energia on pienin. Seuraavan tilan [[$n=2$]] energia on [[$E_2=-\dfrac{1}{2^2}\cdot 13,6\text{ eV}=-3,4\text{ eV}$]]. Tätä kutsutaan ensimmäiseksi viritystilaksi. Energiat ovat negatiivisia, koska elektroni on sidottu atomiytimeen. Jos elektronille annetaan riittävästi energiaa niin, että sen energia kasvaa positiiviseksi, elektroni irtoaa ytimestä ja vetyatomi ionisoituu.

Emissio ja absorptio

Koska vetyatomin elektronin energialla on vain tiettyjä arvoja, se voi siirtyä yhdestä energiatilasta toiseen vain saamalla tai luovuttamalla juuri sopivan energian. Energian suuruus on yhtä suuri kuin tilojen energioiden erotus. Tämä energia saadaan absorboimalla fotoni tai luovutetaan emittoimalla fotoni. Energian ja aallonpituuden välisestä yhteydestä [[$E=\dfrac{hc}{\lambda}$]] seuraa, että fotonin aallonpituudella on myös tietyt arvot. Siirtymistä ylemmälle energiatilalle kutsutaan virittymiseksi ja siirtymistä takaisin alemmalle energiatilalle viritystilan purkautumiseksi.

Virittymiseen vaadittuja tai viritystilan purkautumisessa vapautuvia energioita on helppo määrittää, kun ensin on määritetty siirtymään liittyvien energiatilojen arvot. Oheiseen kaavioon on merkitty kaavalla [[$E_n=-\dfrac{1}{n^2}\cdot 13,6\text{ eV}$]] laskettuja energiatiloja. Tarkastellaan, millainen fotoni tarvitaan virittämään perustilassa oleva vetyatomi ensimmäiselle viritystilalle.

Fotonin energian on oltava

[[$ \quad E_\text{fotoni}=E_2-E_1=-3,4\text{ eV}-\left(-13,6\text{ eV}\right)=10,2\text{ eV}$]].

Lasketaan tätä vastaava aallonpituus: [[$E_\text{fotoni}=\dfrac{hc}{\lambda}$]], joten

[[$ \quad \lambda=\dfrac{hc}{E_\text{fotoni}}=\dfrac{4,136\cdot 10^{-15}\text{ eVs}\cdot 2,998\cdot 10^8\text{ m/s}}{10,2\text{ eV}}=1,215\dotso\cdot 10^7\text{ m}\approx 122\text{ nm}$]]

Tämä on ultraviolettisäteilyä. Jos vetyatomiin kohdistuu juuri tällaista säteilyä, säteily absorboituu vetyatomiin ja elektroni virittyy. Vastaavasti viritystilan purkautuessa vetyatomi emittoi tätä aallonpituutta olevan fotonin.

Emittoituvan tai absorboituvan fotonin aallonpituus

Fotonin energian täytyy olla yhtä suuri kuin elektronin kahden energiatilan erotus: [[$E_\text{fotoni}=\Delta E$]]

Fotonin aallonpituus ratkaistaan energiaerotuksesta fotonin energian ja aallonpituuden välisen yhteyden avulla.

[[$\quad E_\text{fotoni}=\dfrac{hc}{\lambda}$]]

[[$ \quad \lambda=\dfrac{hc}{\Delta E}$]]

Viivaspektrin synty

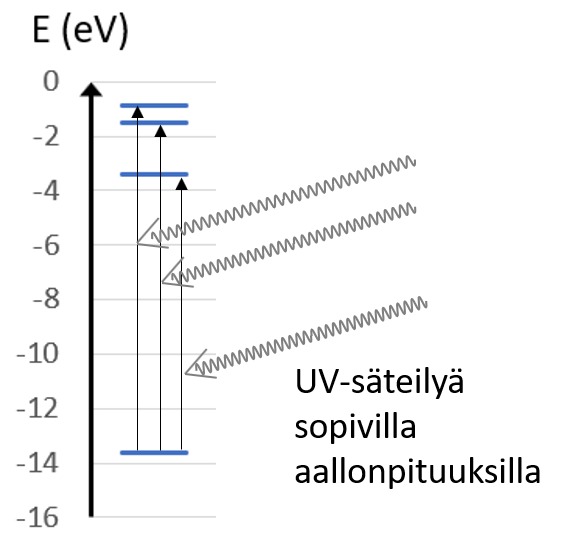Edellisessä kappaleessa laskettiin aallonpituus fotonille, joka virittää vetyatomin elektronin perustilasta ensimmäiselle viritystilalle. Vety absorboi tätä aallonpituutta olevia fotoneja, mutta myös fotoneja, jotka virittävät elektronin korkeammille viritystiloille. Näissä siirtymissä tilojen välinen energiaero on suurempi ja fotonilta vaadittu aallonpituus siten pienempi. Absorboituvat aallonpituudet muodostavat viivaspektrin UV-alueelle. Absorptio ilmenee vetykaasun absorptiospektrissä tummina viivoina, puuttuvina aallonpituuksina. Muunlaiset fotonit eivät vuorovaikututa vetykaasun kanssa, vaan kulkevat kaasun läpi. Oikealla on kaaviokuva energiatasojen välisistä siirtymistä absorptiossa.

Viritystilat purkautuvat nopeasti takaisin perustilaan. Tällöin vapautuu energiaa, mikä havaitaan emittoituvina fotoneina. Vapautuvan energian suuruus ja fotonin aallonpituus riippuvat siitä, miltä viritystilalta elektroni palaa perustilaan. Mahdolliset emittoituvat aallonpituudet ovat samat, kuin mitä vety voi absorboida. Emissiospektrissä havaitaan kuitenkin myös muita aallonpituuksia. Elektronin ei tarvitse palata suoraan perustilaan, vaan se voi esimerkiksi siirtyä 3. viritystilalta ensin 1. viritystilalle ja vasta sitten perustilalle. Mahdollisia siirtymiä on siten enemmän kuin absorptiospektrissä. Koska viritystilat purkaantuvat nopeasti, on epätodennäköistä, että virititystilalla oleva elektroni absorboi sopivan fotonin virittyäkseen korkeammalle energiatilalle. Täten nämä viivat näyttävät puuttuvan absorptiospektristä.

Eri siirtymiä ja vapautuvaa säteilyä on havainnollistettu allaolevassa kuvassa. On syytä huomata, että viritystilojen väliset energiaerot ovat huomattavasti pienempiä kuin viritystilojen ja perustilan väliset erot. Pienempi energia tarkoittaa suurempaa aallonpituutta, ja siten vedyn emissiospektrissä on mukana UV-säteilyn lisäksi näkyvää valoa ja infrapunasäteilyä.