3. FUNKTIO
Määritelmä
Funktio on sääntö, joka liittää lähtöjoukon alkion johonkin maalijoukon alkioon
Funktion lähtö- ja maalijoukot jätetään usein merkitsemättä, jos ne voidaan päätellä asiayhteydestä. Tällä kurssilla funktiot ovat yleensä kuvauksia reaaliluvuilta reaaliluvuille.
Funktion nimeäminen ja funktion arvon laskeminen
Lausekkeen [[$3x-5$]] arvo riippuu muuttujasta [[$x$]]. Jos nimeämme kyseisen lausekkeen vaikkapa kirjaimella [[$f$]], niin merkintä [[$f(x)$]] tarkoittaa funktiota, jossa on muuttujana [[$x$]] ja jossa funktion arvo voidaan laskea lausekkeesta [[$3x-5$]].Funktion määritelmän mukaan kuvaus on funktio vain, jos jokaista muuttujan arvoa vastaa tasan yksi arvojoukon piste. Toisin sanoen, funktio ei voi koskaan saada useampaa eri arvoa samalla muuttujan arvolla, vaan jokainen kuvapiste on yksikäsitteinen.
Katso video aiheesta (kesto n. 9 min.)
Video: Funktio ja funktion kuvaaja (Pekka Peura) Funktion kuvaaja
Kuvaajan [[$y=f(x)$]] avulla havainnollistetaan graafisesti, millä tavoin [[$y$]] riippuu muuttujasta [[$x$]].
Kuvaaja on pisteiden [[$(x,f(x))$]] joukko
- Funktion kuvaaja saadaan piirrettyä, kun asetetaan [[$y = f(x)$]].
- Käydään läpi kaikki määrittelyjoukkoon kuuluvat muuttujan [[$x$]] arvot ja lasketaan niitä vastaavat funktion arvot.
- Piirretään muuttujan [[$x$]] kohdalle piste siihen y-akselin kohtaan, mikä vastaa funktion arvoa kohdassa [[$x$]].
- Kuvaaja muodostuu siis pisteistä [[$(x,y)$]], joissa y-koordinaatti on funktion [[$f$]] arvo kohdassa [[$x$]].
- Kuvaajan pisteet ovat muotoa [[$(x,f(x))$]].
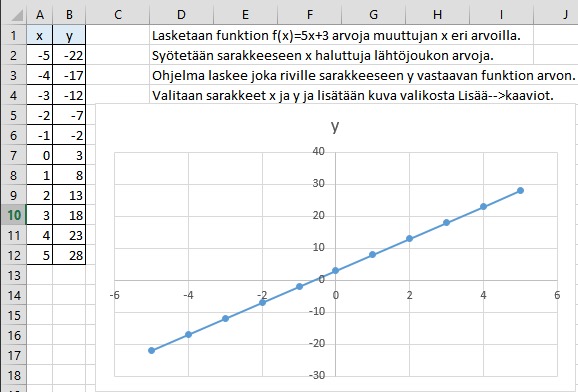
Kuvaajan piirto taulukkolaskentaohjelmalla
- Luodaan muuttujasarake [[$x$]]
- Lasketaan vastaavat funktion arvot sarakkeeseen [[$y$]]
- Muodostetaan [[$x$]] ja [[$y$]] -sarakkeista graafi, eli piirretään pisteet xy-koordinaatistoon
Kuvaajan piirto GeoGebralla
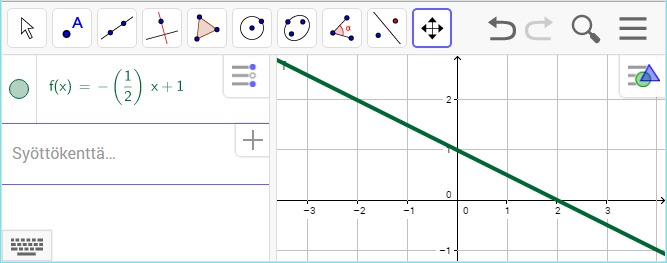GeoGebra -ohjelma piirtää funktion kuvaajan, kun funktio kirjoitetaan syöttökenttään. Kokeile itse erilaisten funktioiden kuvaajien piirtoa osoitteessa: http://web.geogebra.org/#algebra. Voit muuttaa funktiota klikkaamalla syöttämäsi funktion lauseketta.Kuvaajan tulkitseminen, kuvaajan [[$y=f(x)$]] piste [[$(x,y)$]]
on piste [[$\left(x,f(x)\right)$]]
- muuttuja-akseli on [[$x$]]-akseli
- funktion arvoakseli on [[$y$]]-akseli
- Selvitä yllä olevan sovelman avulla, mikä on lausekkeen [[$\frac{1}{8}\cdot 2^3$]] arvo.
- Selvitä millä muuttujan [[$x$]] arvolla pätee [[$x=\frac{1}{8}\cdot x^3$]].
Määrittely- ja arvojoukko
Kaksi funktiota [[$f_1$]] ja [[$f_2$]] ovat samat, jos niillä on samat määrittelyjoukot ja molemmat funktiot saavat samat arvot kaikilla määrittelyjoukon alkioilla.
Funktion määrittelyjoukko [[$M_f$]]
Funktion määrittelyjoukolla ilmaistaan, mitä arvoja funktion lausekkeessa oleva muuttuja voi saada. Toisin sanoen määrittelyjoukkoon kuuluvat kaikki ne muuttujan arvot, joilla funktion arvo voidaan laskea.Funktion arvojoukko [[$ A_f$]]
Funktion arvojoukolla tarkoitetaan kaikkien funktion arvojen muodostamaa joukkoa, joita funktio voi määrittelyjoukossaan saada. Toisin sanoen arvojoukkoon kuuluvat kaikilla mahdollisilla muuttujan arvoilla lasketut funktion arvot.Esimerkkinä potenssifunktio
Määritelmä
Funktiota
[[$$ f(x)=a\cdot x^p, \qquad a\neq 0$$]]
kutsutaan potenssifunktioksi. Eksponenttia [[$p$]] kutsutaan potenssifunktion asteeksi.
Potenssifunktion määrittelyjoukko riippuu asteesta [[$p$]]. Mikäli [[$p$]] on positiivinen kokonaisluku, funktio on määritelty kaikilla reaaliluvuilla. Mikäli [[$p$]] on murtoluku tai irrationaaliluku, määrittelyjoukko joudutaan rajoittamaan ei-negatiivisiin reaalilukuihin. Tällä kurssilla käsitellään vain sellaisia potenssifunktioita, joiden eksponentti on kokonaisluku. Näihin palataan myöhemmin potenssimerkinnän yhteydessä.
Esimerkkinä eksponenttifunktio
Potenssifunktiossa [[$f(x) = x^n$]] muuttuja [[$x$]] on kantalukuna. Jos muuttuja [[$x$]] on sen sijaan eksponenttina, saadaan joukko funktioita, joita kutsutaan eksponenttifunktioiksi.
Määritelmä
Määritelmä
Funktiota [[$$f(x)=a^x, \qquad a>0 \text{ ja } a\ne 1 $$]]
kutsutaan eksponenttifunktioksi. Muuttuja [[$x$]] on eksponenttina ja lukua [[$a$]] kutsutaan kantaluvuksi.
Huomaa, että funktiota [[$1^x$]] ei luokitella eksponenttifunktioksi, vaikka funktio [[$1^x$]] on määritelty. Syy tähän on se, että [[$f(x)=1^x$]] on suora [[$y=1$]].
Eksponentiaalinen muutos
Mikäli jokin arvo kertautuu vakiokertoimella tietyin tarkasteluvälein, muutos on eksponentiaalista. Tällöin suureen arvoa kuvaa eksponenttifunktio. Mikäli opettaja antaa kotitehtäviä aina edelliseen viikkoon verrattuna kaksinkertaisesti, on muutos eksponentiaalista. Jos ensimmäisellä viikolla on kolme kotitehtävää, on seuraavalla 6, seuraavalla 12, seuraavalla 24... Vertaa lineaariseen muutokseen, jossa muutos olisi sama jokaisella viikolla. Esimerkiksi aluksi 3 tehtävää, seuraavalla viikolla 5, seuraavalla 7, seuraavalla 9...
Esimerkki 1. Onko kyseessä funktio?
Mitkä seuraavista ovat funktioita joukolta A joukolle B?
Ratkaisu:
a) Kyseessä on funktio joukolta A joukolle B, sillä jokaista joukon A alkiota (lukua) vastaa täsmälleen yksi joukon B alkio.
b) Kyseessä on funktio joukolta A joukolle B, sillä jokaista joukon A alkiota (lukua) vastaa täsmälleen yksi joukon B alkio. Huomaa, että funktio voi saada saman arvon useilla määrittelyjoukon arvolla.
c) Kyseessä ei ole funktio, sillä alkiolla 2 ei ole yksikäsitteistä kuvaa.
d) Kyseessä ei ole funktio joukolta A joukolle B, sillä luvulla 2 ja 4 ei ole kuvaa.
Ratkaisu:
a) Kyseessä on funktio joukolta A joukolle B, sillä jokaista joukon A alkiota (lukua) vastaa täsmälleen yksi joukon B alkio.
b) Kyseessä on funktio joukolta A joukolle B, sillä jokaista joukon A alkiota (lukua) vastaa täsmälleen yksi joukon B alkio. Huomaa, että funktio voi saada saman arvon useilla määrittelyjoukon arvolla.
c) Kyseessä ei ole funktio, sillä alkiolla 2 ei ole yksikäsitteistä kuvaa.
d) Kyseessä ei ole funktio joukolta A joukolle B, sillä luvulla 2 ja 4 ei ole kuvaa.
Esimerkki 2. Erilaisia funktioita
Funktio [[$osake(t)$]] esittää osakkeen arvoa euroina ajan [[$t$]] funktiona. Funktio [[$a(p)$]] esittää erään kurssin arvosanaa kurssin pisteiden funktiona ja [[$T(l)$]] esittää heilurin heilahdusaikaa langan pituuden funktiona. Määritä osakkeen arvo kesäkuun 15. päivänä, [[$a(20)$]] ja heilahdusaika 2 metrin pituisella langalla.
[[$ a(p) = \begin{cases} 4, \quad 0 \leq p < 12 \\5, \quad 12\leq p < 15 \\ 6, \quad 15\leq p < 18 \\ 7, \quad 18\leq p < 21\\8, \quad 21\leq p < 24\\9, \quad 24\leq p < 27\\10, \quad 27\leq p < 32 \end{cases} $]]
[[$ T(l) = 2\pi \sqrt{\dfrac{\text{l}}{\text{9,80665} \dfrac{\text{m}}{\text{s}^2}}} $]]
Ratkaisu:
Funktion [[$osake(t)$]] kuvaajasta katsomalla nähdään, että kesäkuun puolessa välissä osakkeen arvo on noin 13,1 euroa.
Funktio [[$a(p)$]] on esimerkki paloittain määritellystä funktiosta. Funktion arvoa laskiessa arvo lasketaan sen mukaan, mille välille muuttuja [[$p$]] kuuluu. Muuttuja [[$p$]] on välillä [[$18\leq p<21$]], joten funktion arvo on 7. Kokeile määritellä paloittain määritelty funktio laskimelle tai tietokoneella.
Heilahdusaika 2 metrin pituisella langalla saadaan laskettua, kun sijoitetaan muuttujan arvo lausekkeeseen. Arvoksi saadaan [[$T(2\text{ m})=2\pi\sqrt{\dfrac{2\text{ m}}{9,80665 \dfrac{\text{ m}}{\text{ s}^2}}}\approx 2,8\text{ s}$]]. Kokeile käytännössä! Tarvitset vain lankaa, punnuksen ja kellon.
[[$ a(p) = \begin{cases} 4, \quad 0 \leq p < 12 \\5, \quad 12\leq p < 15 \\ 6, \quad 15\leq p < 18 \\ 7, \quad 18\leq p < 21\\8, \quad 21\leq p < 24\\9, \quad 24\leq p < 27\\10, \quad 27\leq p < 32 \end{cases} $]]
[[$ T(l) = 2\pi \sqrt{\dfrac{\text{l}}{\text{9,80665} \dfrac{\text{m}}{\text{s}^2}}} $]]
Ratkaisu:
Funktion [[$osake(t)$]] kuvaajasta katsomalla nähdään, että kesäkuun puolessa välissä osakkeen arvo on noin 13,1 euroa.
Funktio [[$a(p)$]] on esimerkki paloittain määritellystä funktiosta. Funktion arvoa laskiessa arvo lasketaan sen mukaan, mille välille muuttuja [[$p$]] kuuluu. Muuttuja [[$p$]] on välillä [[$18\leq p<21$]], joten funktion arvo on 7. Kokeile määritellä paloittain määritelty funktio laskimelle tai tietokoneella.
Heilahdusaika 2 metrin pituisella langalla saadaan laskettua, kun sijoitetaan muuttujan arvo lausekkeeseen. Arvoksi saadaan [[$T(2\text{ m})=2\pi\sqrt{\dfrac{2\text{ m}}{9,80665 \dfrac{\text{ m}}{\text{ s}^2}}}\approx 2,8\text{ s}$]]. Kokeile käytännössä! Tarvitset vain lankaa, punnuksen ja kellon.
Esimerkki 3. Määrittely- ja arvojoukko
Määritä seuraavien funktioiden määrittely- ja arvojoukot
a) [[$f_1(x)=x^4$]]
b) [[$f_2(x)=2x$]]
c) [[$f_3(x)=-2^x$]].
Ratkaisu:
a) Funktion [[$f_1(x)=x^4$]] arvo voidaan laskea kaikilla reaaliluvuilla, joten funktion määrittelyjoukko on reaalilukujen joukko [[$\mathbb{R}$]]. Koska kyseessä on parillinen eksponentti, kaikki funktion arvot ovat ei-negatiivisia. Eikä ole olemassa sellaista ei-negatiivista arvoa, jota funktio ei saisi, joten funktion arvojoukko on kaikkien ei-negatiivisten lukujen joukko.
b) Funktion [[$f_2(x)=2x$]] arvo voidaan laskea kaikilla reaaliluvuilla. Funktio saa myös kaikki reaalilukuarvot, joten funktion määrittely- ja arvojoukko on reaalilukujen joukko [[$\mathbb{R}$]]
c) Funktion [[$f_3(x)=-2^x$]] määrittelyjoukko on reaalilukujen joukko, sillä funktion arvo voidaan laskea kaikilla reaaliluvuilla. Funktio [[$2^x$]] saa ainoastaan positiivisia arvoja, joten funktio [[$f_3(x)=-2^x$]] saa ainoastaan negatiivisia arvoja. Funktio myös saa kaikki negatiiviset reaalilukuarvot, joten arvojoukko on negatiivisten reaalilukujen joukko. Huomaa, että luku nolla ei kuulu arvojoukkoon, sillä [[$f_3(x)=-2^x$]] ei ole millään muuttujan [[$x$]] arvolla nolla.
a) [[$f_1(x)=x^4$]]
b) [[$f_2(x)=2x$]]
c) [[$f_3(x)=-2^x$]].
Ratkaisu:a) Funktion [[$f_1(x)=x^4$]] arvo voidaan laskea kaikilla reaaliluvuilla, joten funktion määrittelyjoukko on reaalilukujen joukko [[$\mathbb{R}$]]. Koska kyseessä on parillinen eksponentti, kaikki funktion arvot ovat ei-negatiivisia. Eikä ole olemassa sellaista ei-negatiivista arvoa, jota funktio ei saisi, joten funktion arvojoukko on kaikkien ei-negatiivisten lukujen joukko.
b) Funktion [[$f_2(x)=2x$]] arvo voidaan laskea kaikilla reaaliluvuilla. Funktio saa myös kaikki reaalilukuarvot, joten funktion määrittely- ja arvojoukko on reaalilukujen joukko [[$\mathbb{R}$]]
c) Funktion [[$f_3(x)=-2^x$]] määrittelyjoukko on reaalilukujen joukko, sillä funktion arvo voidaan laskea kaikilla reaaliluvuilla. Funktio [[$2^x$]] saa ainoastaan positiivisia arvoja, joten funktio [[$f_3(x)=-2^x$]] saa ainoastaan negatiivisia arvoja. Funktio myös saa kaikki negatiiviset reaalilukuarvot, joten arvojoukko on negatiivisten reaalilukujen joukko. Huomaa, että luku nolla ei kuulu arvojoukkoon, sillä [[$f_3(x)=-2^x$]] ei ole millään muuttujan [[$x$]] arvolla nolla.
