Geometria
Kolmion geometrian kertausta
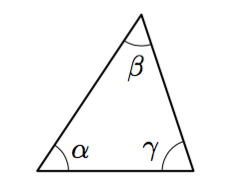
Tapana on merkitä kulmia kreikkalaisilla aakkosilla, kuten tässäkin kolmiossa. Mikäli halutaan nimetä kolmion kärkiä, Niille annetaan vastaavasti ISOT kirjaimet A, B ja C jne. Edelleen sivuille annetaan nimet pienillä kirjaimilla.
Kolmion kulmien summa on aina:
[[$ \alpha+\beta+\gamma=180^{\circ}$]]
Suorakulmaisessa kolmiossa on nimensä mukaisesti yksi suora kulma.
Myös trigonometriset funktiot toimivat vain suorakulmaisessa kolmiossa. Niiden avulla voi ratkaista kulman suuruutta tai sivun pituutta.
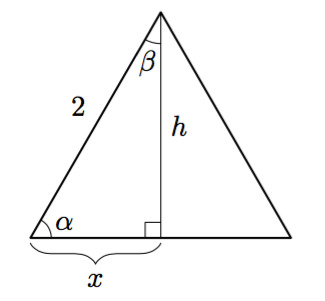
Laske kuvan kolmion korkeus, kun x = 0,8.
Kuva kisallioppiminen.fi
Ratkaisu:
Muodostetaan Pythagoraan lause ja ratkaistaan se:
[[$$ \begin{split} 0,8^{2}+h^{2}&=2^{2} ~~ |- 0,8^{2}\\ h^{2}&=2^{2}-0,8^{2}\\ h^{2}&=3,36 ~~ | \sqrt{}\\ h&= \sqrt{3,36} \\ &\approx 1,8 \end{split}$$]]
Korkeus on siis 1,8.
Ratkaisu:
Jompi kumpi kulmista on ratkaistava trigonometrisen funktion avulla. Valitaan vaikka α. Valitaan sopiva trigonometrinen yhtälö:
[[$$ \begin{split} \cos\alpha&=\frac{0,8}{2}\\ &=0,4 ~~|cos^{-1}\\ \alpha&\approx 66 ^{\circ} \end{split} $$]]
Nyt kun tiedetään α-kulman suuruus, voidaan β laskea vähennyslaskulla:
[[$$ β= 180 ^{\circ}-90^{\circ}-66^{\circ}=34^{\circ} $$]]
Kolmion kulmien summa on aina:
[[$ \alpha+\beta+\gamma=180^{\circ}$]]
Kuva kisallioppiminen.fi
Suorakulmaisessa kolmiossa on nimensä mukaisesti yksi suora kulma.
Kuva kisallioppiminen.fi
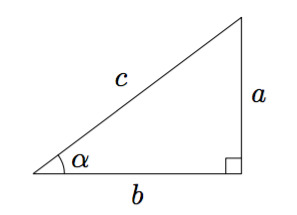
Suorakulmaiseen kolmioon voidaan soveltaa pariakin sääntöä. Ensimmäinen niistä on Pythagoraan lause:[[$ a^{2}+b^{2}=c^{2}$]]
Myös trigonometriset funktiot toimivat vain suorakulmaisessa kolmiossa. Niiden avulla voi ratkaista kulman suuruutta tai sivun pituutta.
[[$ \sin\alpha=\frac{a}{c}\\$]]
[[$ \cos\alpha=\frac{b}{c}\\$]]
[[$ \tan\alpha=\frac{a}{b}\\$]]
Esimerkki 1:
Laske kuvan kolmion korkeus, kun x = 0,8.
Kuva kisallioppiminen.fiRatkaisu:
Muodostetaan Pythagoraan lause ja ratkaistaan se:
[[$$ \begin{split} 0,8^{2}+h^{2}&=2^{2} ~~ |- 0,8^{2}\\ h^{2}&=2^{2}-0,8^{2}\\ h^{2}&=3,36 ~~ | \sqrt{}\\ h&= \sqrt{3,36} \\ &\approx 1,8 \end{split}$$]]
Korkeus on siis 1,8.
Esimerkki 2:
Ratkaise edellisen esimerkin kolmion kulmat α ja β.Ratkaisu:
Jompi kumpi kulmista on ratkaistava trigonometrisen funktion avulla. Valitaan vaikka α. Valitaan sopiva trigonometrinen yhtälö:
[[$$ \begin{split} \cos\alpha&=\frac{0,8}{2}\\ &=0,4 ~~|cos^{-1}\\ \alpha&\approx 66 ^{\circ} \end{split} $$]]
Nyt kun tiedetään α-kulman suuruus, voidaan β laskea vähennyslaskulla:
[[$$ β= 180 ^{\circ}-90^{\circ}-66^{\circ}=34^{\circ} $$]]
Pinta-aloja
Myös sekalaisia pinta-alaan ja tilavuuteen liittyviä geometrisia probleemia on ainakin vanhoissa pääsykokeissa nähty. Alla joitain esimerkkejä.
Ratkaisu:
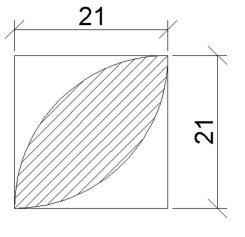
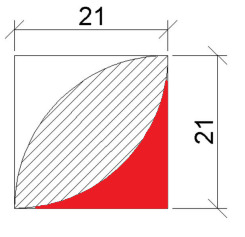
Viivoitetun alueen muodostavat kaaret ovat sellaisen ympyrän kaaria, jonka säde on 21 cm. Koko muodon ulkoreunat muodostavat neliön, jonka särmä on 21 cm.
Lasketaan ensin neliön pinta-ala neliödesimetreinä:
[[$ A_{neliö}=2,1 ~dm\cdot2,1~dm=4,41~dm^2 $]]
Lasketaan sitten 1/4 ympyrän pinta-ala:
[[$ A_{sektori}=\frac{1}{4}\cdot\pi r^2=\frac{1}{4}\cdot\pi \cdot (2,1 ~dm)^2~=3,463... ~dm^2 $]]
Lasketaan edellämainittujen erotus, joka on siis nyt tuo värillä korostettu alue.
[[$ A_{neliö}- A_{sektori}=4,41~dm^2-3,463... ~dm^2=0,946... ~dm^2 $]]
Kuvasta näkee, että koko neliö koostuu kolmesta osasta. Kun reunapalat vähentää neliön pinta-alasta, saadaan viivoitetun alueen pinta-ala:
[[$ A_{viivoitettu ~alue}=4,41~dm^2-2\cdot 0,946...~dm^2\approx 2,5 ~dm^2$]]
Esimerkki 3.
Laske viivoitetun alueen pinta-ala. Ilmoita vastaus neliödesimetreinä, yhden desimaalin tarkkuudella. Kuvan mitat on ilmoitettu senttimetreinä.
Ratkaisu:
Viivoitetun alueen muodostavat kaaret ovat sellaisen ympyrän kaaria, jonka säde on 21 cm. Koko muodon ulkoreunat muodostavat neliön, jonka särmä on 21 cm.
Lasketaan ensin neliön pinta-ala neliödesimetreinä:
[[$ A_{neliö}=2,1 ~dm\cdot2,1~dm=4,41~dm^2 $]]
Lasketaan sitten 1/4 ympyrän pinta-ala:
[[$ A_{sektori}=\frac{1}{4}\cdot\pi r^2=\frac{1}{4}\cdot\pi \cdot (2,1 ~dm)^2~=3,463... ~dm^2 $]]
Lasketaan edellämainittujen erotus, joka on siis nyt tuo värillä korostettu alue.
[[$ A_{neliö}- A_{sektori}=4,41~dm^2-3,463... ~dm^2=0,946... ~dm^2 $]]Kuvasta näkee, että koko neliö koostuu kolmesta osasta. Kun reunapalat vähentää neliön pinta-alasta, saadaan viivoitetun alueen pinta-ala:
[[$ A_{viivoitettu ~alue}=4,41~dm^2-2\cdot 0,946...~dm^2\approx 2,5 ~dm^2$]]