The Pythagorean theorem can be used to solve any of the side lengths of a triangle if the lengths of its two other sides are known. When placing a value in a Pythagorean theorem, one must be careful to place the lengths of the legs and the length of the hypotenuse in their correct places. The unknown variable is then solved according to normal equation-solving rules.

Example 1

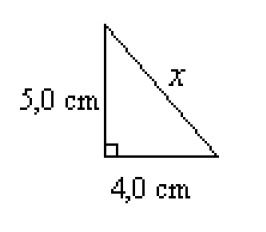
Calculate the length of the hypotenuse of the adjacent right triangle. The lengths of the legs are known.

Place the length of the sides in the Pythagorean theorem.

 

[[$ x^2 = 4,0^2 + 5,0^2 $]]​
[[$ x^2 = 16,0 + 25,0 $]]​
[[$ x^2 = 41,0 $]]​	Taking a square root cancels raising a number to its square. Because of this, we can remove the power of x by taking a square root from both sides of the equation.
[[$ x = \sqrt{41,0} $]]​
[[$ x \approx 6,4 $]]​

Answer: The length of the hypotenuse is [[$ 6,4 $]] cm.

Example 2

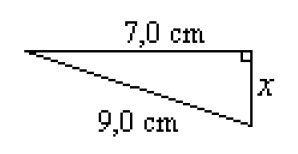
Calculate the side length [[$ x $]] from the adjacent right triangle.

Since the triangle is a right triangle, the Pythagorean theorem can be applied. The side whose length is requested is a leg. The other leg has a length of [[$ 7,0 $]] cm. The length of the hypotenuse is [[$ 9,0 $]] cm.

[[$ \quad \begin{align} x^2 + 7,0^2 &= 9,0^2 \\ \\ x^2 &= 9,0^2 - 7,0^2 \\ \\ x^2 &= 32,0 \\ \\ x &= \sqrt{32,0} \\ \\ x &\approx 5,7 \end{align} $]]​

Answer: The side [[$ x $]] is [[$ 5,7 $]] cm long.

Example 3

The coordinates of point [[$ A $]] are ([[$ -4, 1 $]]) and the coordinates of point [[$ B $]] ([[$ 2, 3 $]]). Calculate how far the two points are from one another.

Solution:

Place the points [[$ A $]] and [[$ B $]] in the coordinate system and connect them with a line segment. Complete the pattern into a right triangle.

The distance between the points is the length of the triangle's hypotenuse. This can be calculated using the Pythagorean theorem.

[[$ \quad \begin{align} AB^2 &= 6^2 + 2^2 \ \\ AB^2 &= 36 + 4 \ \\ AB^2 &= 40 \ \\ AB &= \sqrt{40} \ \\ AB &\approx 6,3 \end{align} $]]​

Answer: The distance between point [[$ A $]] and point [[$ B $]] is [[$ 6,3 $]].