7. Rotation and translation
Rotation and translation
Translation
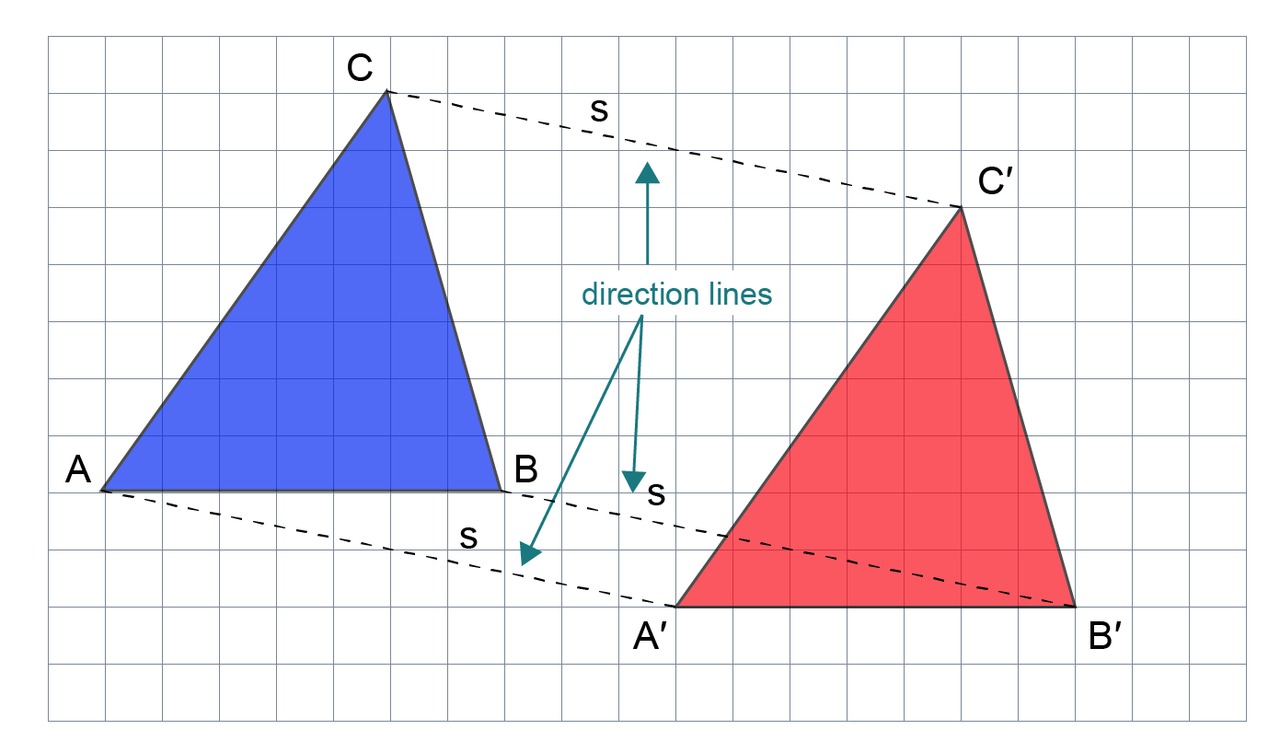
In translation orparallel transportation, all the points of a figure are moved an equal distance in the same direction.Example 1
Move the triangle [[$ ABC $]] in the direction [[$ s $]] = ”[[$ 2 $]] units down and [[$ 10 $]] units to the right".
Rotation
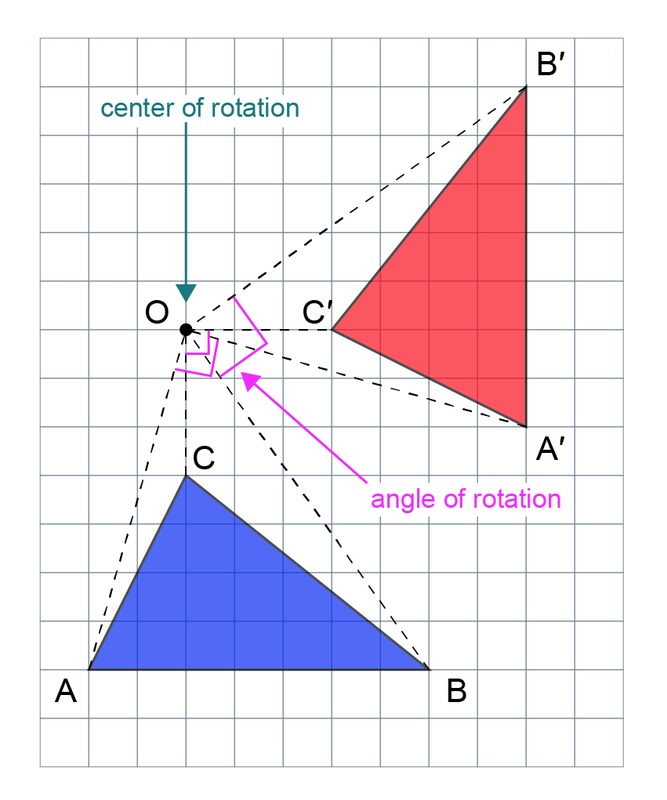
In rotation, each point of a figure is rotated around a center of rotation. Each point is rotated by the angle of rotation [[$ \ alpha $]] [[$ O $]], so that the distance between each point and the center of rotation [[$ O $]] remains the same.A rotationally symmetric figure is reflected as a rotation of the angle [[$ \ alpha $]] for itself, in which case it is said that the figure is symmetric with respect to rotation at an angle of [[$ \ alpha $]].
Example 2
Rotate the triangle [[$ ABC $]] counterclockwise by [[$ 90 $]] degrees around point [[$ O $]].
Example 3
If the adjacent figure is rotated around its center by [[$ 180 ° $]], it will look exactly the same as the original pattern, and it will be in exactly the same place. Therefore, the figure can be considered rotationally symmetric at an angle of [[$ 180 ° $]].
Since a [[$ 180 ° $]] rotation with respect to the figure's center can be performed twice before a full rotation is reached, the figure's order of rotational symmetry is two.
Exercises
Basic exercises
Applied exercises
Challenging exercises
3/07. Submission folder for answers
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.