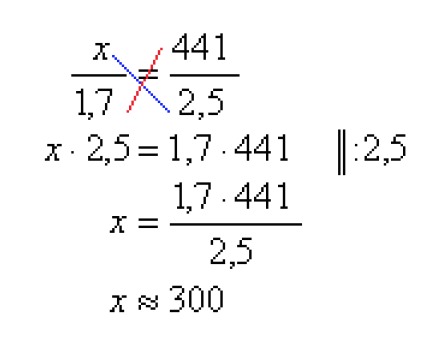3. The similarity of triangles
The similarity of triangles
If a triangle is divided into two parts by some line parallel to the side of the triangle, a triangle within the original triangle, or [[$ ABC \sim DBE $]], is formed.
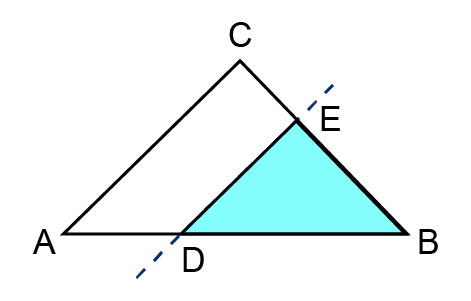
The triangles [[$ ABC $]] and [[$ DBE $]] are similar if all their opposite angles are equal to each other.
However, when analysing similarities, it is sufficient to show only two corresponding angles as equal. Since the sum of the angles of the triangle is [[$ 180° $]], the remaining corresponding angles must also be equal.
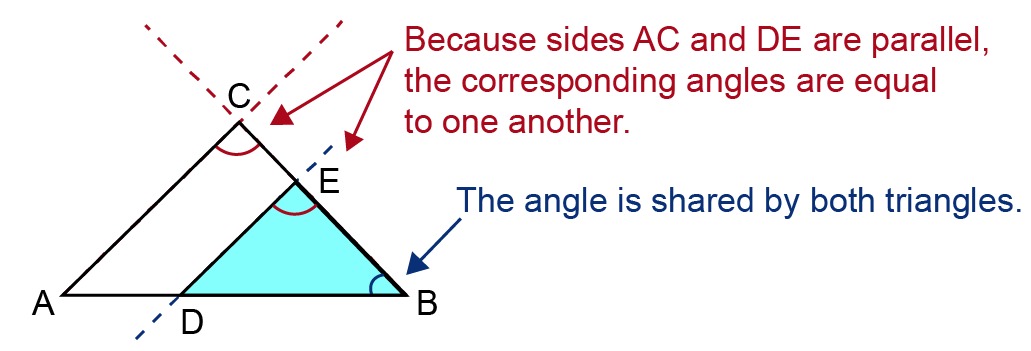
Once the similarity of the two triangles has been proven, all the corresponding sides of the triangle can be compared with one another. The length ratio of the two triangles is obtained by comparing any of their corresponding side pairs.
[[$ \displaystyle\frac {AC} {DE} = \displaystyle\frac {CB} {EB} = \displaystyle\frac {AB} {DB} $]]
Example 1
The length of the shadow of a person [[$ 1,7 $]] m long is [[$ 2,5 $]] m. At the same time, the length of the shadow of the Eiffel Tower is [[$ 441 $]] m. How high is the tower?
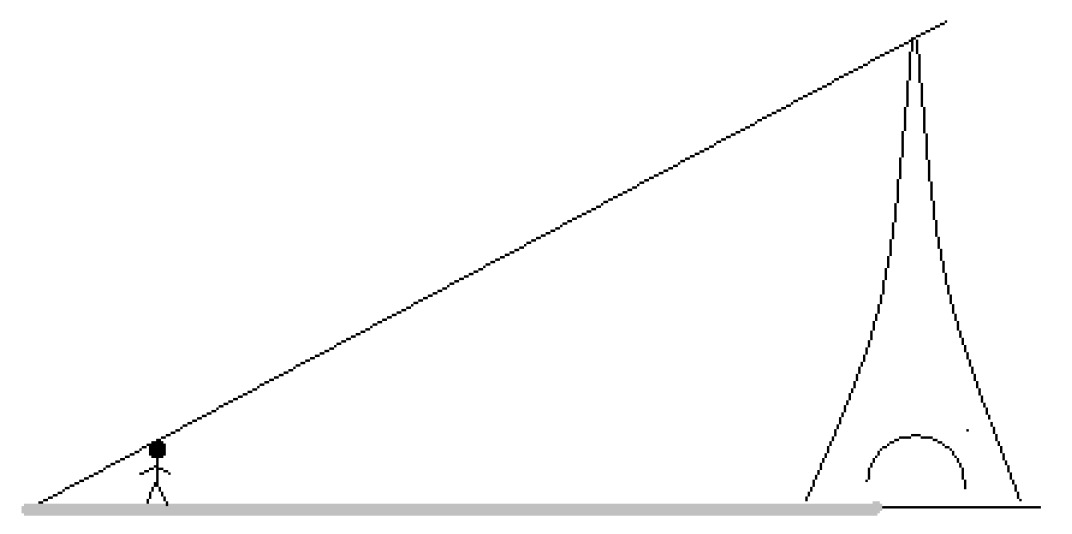
In the example, two similar triangles are formed, since the angle between the beam of light and the ground is the same in both cases. In addition, the Eiffel Tower and the person are perpendicular to the ground.
The ratio of the length of the Eiffel Tower and the length of the person is the same as the ratio of the lengths of the two shadows. As a result of this, we get the following comparison:
[[$ \displaystyle\frac {x} {{1,7} \text {m}} = \displaystyle\frac {{441} \text{m}} {{2,5} \text{m}} $]]
This can be solved with cross multiplication:
Exercises
Basic exercises
Applied exercises
Challenging exercises
3/03. Submission folder for answers
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.