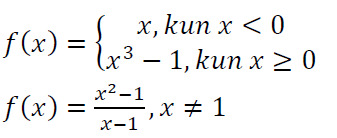Sähköisten välineiden ohjeita ja harjoittelua
7.10.2019 Tehtäviä
Harjoitellaan derivoituvuuden osoittamista ja derivoimista.
funktion määrittely
Raja-arvoja tarvitaan usein:
Teoria (opettele ulkoa)
Funktio f(x) on derivoituva kohdassa a, jos erotusosamäärän raja-arvo
[[$ \lim_{x\rightarrow a}\frac{\displaystyle f\left(x\right)-f\left(a\right)}{\displaystyle x-a} $]]
on olemassa. Eli tuon erotusosamäärän toispuoleiset raja-arvot ovat samat. Lisäksi funktion pitää olla jatkuva kyseisessä kohdassa eli funktion toispuoleiset raja-arvot ovat yhtä suuret funktion arvon kanssa.
Tehdään tehtävä 333. Opettajan johdolla funktio h(x) ja muut funktiot itsenäisesti
Esim 1 tehtävä 333 h(x):
Tehtävä 1 tehtävä 333 funktiot f(x) ja g(x) s.85
Tutki ensin jatkuvuus rajakohdassa. Ja vasta sitten derivoituvuus:
1. tee ensin vasemmanpuoleinen erotusosamäärän raja-arvo:
määritä molemmat palat erikseen, esim. ylempi pala k(x)=-x2+4x
muodosta erotusosamäärä kohdassa x=3 käyttämällä edellisen kohdan määrittelyä
2. tee oikeanpuoleinen erotusosamäärän raja-arvo samalla tavalla
3. vertaile toistpuoleisia erotusosamäärän raja-arvoja
4. Piirrä vielä kuvaaja ja tutki, miltä kuvaaja näyttää kohdassa x=3
Tee sama tehtävän funktiolle g(x). Huomaa, että sinun tarvitsee vain muokata edellisen kohdan oikean puoleista raja-arvoa. Piirrä kuvaaja ja tutki, miltä kuvaaja näyttää kohdassa x=3.
Kuvaaja geogebralla piirrettynä:

Derivaatan eli muutosnopeuden (=tangentin kulmakertoimen ) arvoja on hidas laskea erotusosamäärän avulla. On mahdollista määrittää derivoimalla derivaattafunktio f ' , jonka arvo f ' (x) on funktion derivaatan arvo kohdassa x.
Tehtävä 2 Tutkitaan polynomifunktion ja sen derivaattafunktion kuvaajia
Avaa tiedosto funktio ja sen derivaatta funktio.ggb geogebrassa ja tutki kuvaajia säätämällä liukukytkimiä ja pistettä A.
Vasemmanpuoleinen (piirtoalue 1) on funktion kuvaaja ja oikeanpuoleinen (piirtoalue 2) on derivaattafunktion kuvaaja.
a) Minkälainen on kolmannen asteen funktion derivaattafunktio?
b) Entä toisen asteen?
c) Tutki derivaattafunktion merkkejä ja nollakohtia. Miten ne liittyvät funktion kuvaajaan? Minkälainen on funktion kuvaaja, kun derivaatta on positiivinen? Negatiivinen? Nolla?
Derivaattafunktion selvittämiseksi on olemassa derivoimissääntöjä, joiden avulla derivaattafunktio voidaan selvittää.
Tehtävä 3 Tutkitaan polynomin derivoimissääntöjä
Derivoi erilaisia polynomifunktioita ja koita määrittää derivoimissääntöjä havaintojesi avulla.
geogebralla CAS-laskin toiminto f '
casion laskin math2 [[$ \frac d{dx}() $]]

Jos on vielä aikaa, niin tee tehtävät 336, 337, 339, 340.
Lisätehtävät jos vieläkin on aikaa 348 ja 349
- Asenna SpeedCrunch koneellesi (https://speedcrunch.org/download.html)
- muuta asetuksista näytön teemaksi standard ja fontiksi 12.
funktion määrittely
- A-osan laskin SpeedCrunch
- Classpad Casio
- Geogebra
Raja-arvoja tarvitaan usein:
- Classpad raja-arvo: mat2-valikosta, toispuoleiset raja-arvot saa lisäämällä - tai + rajaluvun jälkeen.
- Geogebra: kirjoittamalla raja saat eri raja-arvojen komennot..
- avaa läksyvihko tai https://math-demo.abitti.fi/
- kirjan tehtävä 330 A-osan välineillä
- mikä on suorien kohtisuoruusehto
- miten voi laskea tangentin kulmakertoimen
- vastaus: tangentin kulmakerrroin = derivaatan arvo kyseisessä kohdassa
- erotusosamäärän raja-arvokaava löytyy koejärjestelmän ohjeista, josta sen voi kopioida klikkaamalla: https://cheat.abitti.fi
- kirjan tehtävä 331b)-kohta A-osan välineillä
- harjoittele funktion määrittäminen SpeedCrunchilla
- harjoittele toisen asteen yhtälön ratkaisukaava SpeedCrunchilla (tekijöihin jako)
Teoria (opettele ulkoa)
Funktio f(x) on derivoituva kohdassa a, jos erotusosamäärän raja-arvo
[[$ \lim_{x\rightarrow a}\frac{\displaystyle f\left(x\right)-f\left(a\right)}{\displaystyle x-a} $]]
on olemassa. Eli tuon erotusosamäärän toispuoleiset raja-arvot ovat samat. Lisäksi funktion pitää olla jatkuva kyseisessä kohdassa eli funktion toispuoleiset raja-arvot ovat yhtä suuret funktion arvon kanssa.
Tehdään tehtävä 333. Opettajan johdolla funktio h(x) ja muut funktiot itsenäisesti
Esim 1 tehtävä 333 h(x):
- poistetaan ensin itseisarvomerkit eli ilmaistaan funktion paloittain merkittynä
- Classpadissa paloittain määrittely työkalu on mat.3 -valikossa, geogebrassa paloittain määrittely kirjoitettiin jos -komennon avulla.
- Geogebralla (tekstirivejä=perusteluita saa kun laittaa riville päälle kirjoitustilan T)
- Casiolla sai toispuoleiset raja-arvot lisäämällä tavalliseen raja-arvoon merkin + tai - .
- Tutkitaan ensin funktion jatkuvuus raja-kohdassa.
- Tämän jälkeen tutkitaan erotusosamäärän toispuoleiset raja-arvot
Tehtävä 1 tehtävä 333 funktiot f(x) ja g(x) s.85
Tutki ensin jatkuvuus rajakohdassa. Ja vasta sitten derivoituvuus:
1. tee ensin vasemmanpuoleinen erotusosamäärän raja-arvo:
määritä molemmat palat erikseen, esim. ylempi pala k(x)=-x2+4x
muodosta erotusosamäärä kohdassa x=3 käyttämällä edellisen kohdan määrittelyä
2. tee oikeanpuoleinen erotusosamäärän raja-arvo samalla tavalla
3. vertaile toistpuoleisia erotusosamäärän raja-arvoja
4. Piirrä vielä kuvaaja ja tutki, miltä kuvaaja näyttää kohdassa x=3
Tee sama tehtävän funktiolle g(x). Huomaa, että sinun tarvitsee vain muokata edellisen kohdan oikean puoleista raja-arvoa. Piirrä kuvaaja ja tutki, miltä kuvaaja näyttää kohdassa x=3.
Kuvaaja geogebralla piirrettynä:

Derivaatan eli muutosnopeuden (=tangentin kulmakertoimen ) arvoja on hidas laskea erotusosamäärän avulla. On mahdollista määrittää derivoimalla derivaattafunktio f ' , jonka arvo f ' (x) on funktion derivaatan arvo kohdassa x.
Tehtävä 2 Tutkitaan polynomifunktion ja sen derivaattafunktion kuvaajia
Avaa tiedosto funktio ja sen derivaatta funktio.ggb geogebrassa ja tutki kuvaajia säätämällä liukukytkimiä ja pistettä A.
Vasemmanpuoleinen (piirtoalue 1) on funktion kuvaaja ja oikeanpuoleinen (piirtoalue 2) on derivaattafunktion kuvaaja.
a) Minkälainen on kolmannen asteen funktion derivaattafunktio?
b) Entä toisen asteen?
c) Tutki derivaattafunktion merkkejä ja nollakohtia. Miten ne liittyvät funktion kuvaajaan? Minkälainen on funktion kuvaaja, kun derivaatta on positiivinen? Negatiivinen? Nolla?
Derivaattafunktion selvittämiseksi on olemassa derivoimissääntöjä, joiden avulla derivaattafunktio voidaan selvittää.
Tehtävä 3 Tutkitaan polynomin derivoimissääntöjä
Derivoi erilaisia polynomifunktioita ja koita määrittää derivoimissääntöjä havaintojesi avulla.
geogebralla CAS-laskin toiminto f '
casion laskin math2 [[$ \frac d{dx}() $]]

Jos on vielä aikaa, niin tee tehtävät 336, 337, 339, 340.
Lisätehtävät jos vieläkin on aikaa 348 ja 349
Geogebra (harjoittelua 27.9.2019)
- tehdään opettajan johdolla tehtävä 142 hyödyntäen sähköisiä apuvälineitä
- Tehtävä 206 (taulukkolaskenta raja-arvolle)
- paloittain määritelty funktio
- Paloittain määriteltyjen funktioiden sekä funktioiden, joiden määrittelyjoukko ei ole koko reaalilukujen joukko, piirtämistä varten GeoGebrassa on komento Jos[]:
- Jos[jos,niin] Jos[ehto, lauseke]
- Jos[jos,niin,muuten] Jos[ehto, lauseke, lauseke muualla]
- Toinen tapa: kirjoita syöttökenttään f(x)=(lauseke)(ehto)+(lauseke)(ehto)
- Kokeile, mitä saat kun piirrät (kopioi syöttökenttään)
- f(x)=Jos[-3<x<3,sin(x)]
- g(x)=Jos[x<1,sin(x),x^2]
- h(x)=(x)(x<0)+(x^3-1)(x>=0)
- Harjoittele paloittain määritellyn funktion piirtämistä seuraavilla tehtävillä (yhtäsuuruusmerkkejä ja erisuurimerkki löytyy syöttökentän alphan alta
- Piirrä (vaihda eri nimi kahdelle funktioille esim. f(x), g(x) ja h(x) ) Seuraavassa tehtävässä jatketaan niiden tutkimista
- Tutki edellisen kohdan funktioita. Onko niillä raja-arvoa kohdassa 0? Jotta raja-arvo olisi olemassa, on vasemman ja oikean puoleisen raja-arvon oltava sama. Eli tutki, mitä arvoa funktion arvot lähestyy, kun x lähestyy nollaa sen oikealta puolelta ja toisaalta vasemmalta puolelta.
- Paloittain määriteltyjen funktioiden sekä funktioiden, joiden määrittelyjoukko ei ole koko reaalilukujen joukko, piirtämistä varten GeoGebrassa on komento Jos[]:
- piirrä kuvaajat geogebralla ja laske käyttämällä geogebran valmista raja-arvo-komentoa (kirjoita raja , niin saat useamman vaihtoehdon, valitse oikea)
- tehtävä 225
- 231
- 236 (liukusäätimellä)
- rationaalilausekkeiden käsittely (kokeile, jos ehdit)
- toiminnot:
- poista sulkeet (esim 108a)
- tekijöihin jako (104b)
- Casion Classpadilla
- simplify (sievennys)
- expand (sulkeiden poisto)
- combine (108c)
- toiminnot:
- rationaaliepäyhtälön ratkaisu
- muista tarkistaa yhtälö (tarkkana sulkeiden kanssa)
- kokeile CAS-laskimella: Millä x:n arvolla funktio [[$ f(x)=\frac{x+1}{x^2-1}$]]a) saa arvon 2 b) on positiivinen?
- Tutki oppikirjan applettia: https://www.geogebra.org/m/sAdxZ4en#material/PFUQJk85
Tutkimustehtäviä
Funktion raja-arvo
- tutki raja-arvoa taulukon avulla antamalla muuttujalle arvoja tutkittavan kohdan molemmilta puolelta (desimaalipilkun sijasta käytä pistettä), ohje appletin ylälaidassa:
- raja-arvo taulukon avulla
- kokeile eri funktioita, onko niillä raja-arvoa palojen rajakohdassa
- selvitä, milloin raja-arvo on olemassa seuraavien tiedostojen avulla: