The slope coefficients of lines can be used to examine whether two lines are parallel or perpendicular to one another. Lines that intersect perpendicularly are called perpendiculars.

Example 1

Examine whether the lines [[$ y = \displaystyle\frac {1} {2}x – 1 $]]​ and [[$ x – 2y + 6 = 0 $]]​ are parallel.

Solution:

The slope of the line [[$ y = \displaystyle\frac {1} {2}x – 1 $]]​ is [[$ \displaystyle\frac {1} {2} $]]​.

Convert the equation [[$ x - 2 y + 6 = 0 $]]​ into its slope-intercept form:

[[$ \quad \begin{align} x - 2y + 6 &= 0 \\ - 2y &= –x – 6 \space ||:(–2) \\ y &= \displaystyle\frac {1} {2}x + 3 \end{align} $]]​

Thus, the slope of the line [[$ x - 2y + 6 = 0 $]]​ is [[$ \displaystyle\frac {1} {2} $]]​.

Answer: Since the two lines have the same slope, the lines are parallel.

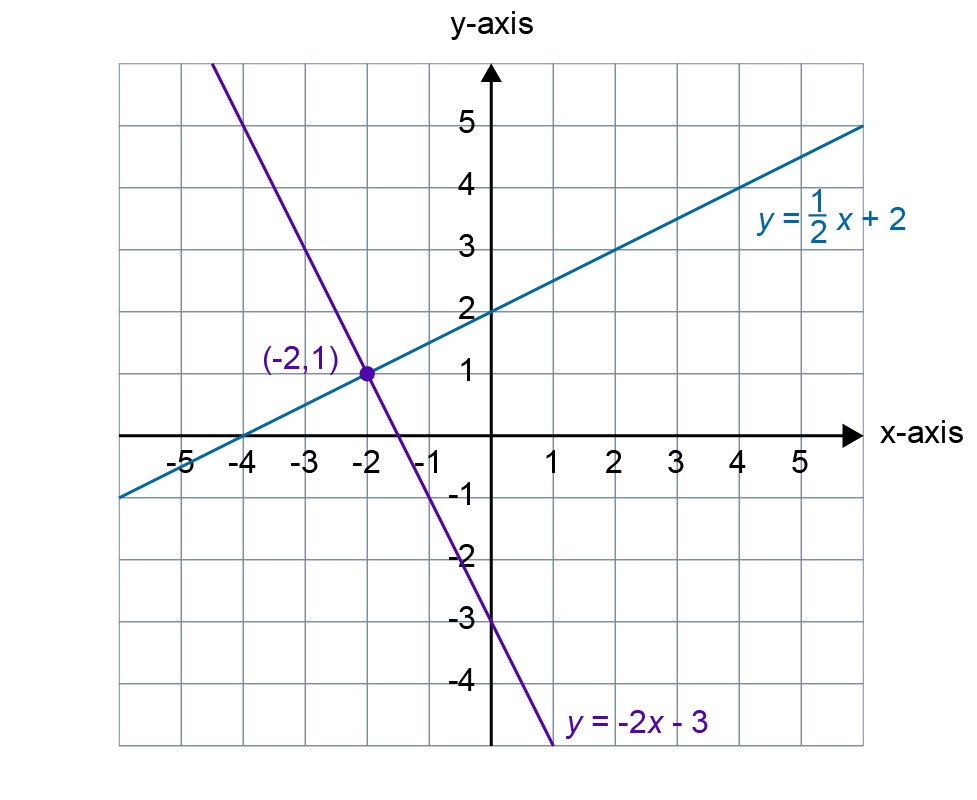
Example 2

Determine the equation of a line that passes through point [[$ (-2, 1) $]] and is perpendicular to the line [[$ y = \displaystyle\frac {1} {2}x + 2 $]]​.

Solution:

The slope of the given line is [[$ \displaystyle\frac {1} {2} $]]​.

Since the lines are perpendicular to one another, the product of their slope must be [[$ –1 $]]. Based on this, an equation can be used to solve the slope of the second line.

[[$ \quad \begin{align} \displaystyle\frac {1} {2} · k &= –1 \space ||· 2 \\ k &= –2 \end{align} $]]​​

Thus, the equation of the line is of the form [[$ y = -2x + b $]]. To solve the constant term [[$ b $]], place the point [[$ (-2, 1) $]] on the line expression, and solve the resulting equation for the variable [[$ b $]].

​[[$ \quad \begin{align}1 &= -2 · (-2) + b \ \\ 1 &= 4 + b \ \\ - b &= 4 -1 \ \\ - b &= 3 \space ||:(–1) \ \\ b &= -3 \end{align} $]]​

Answer: The equation of the line is [[$ y = –2x – 3 $]]​.

The answer can be checked by drawing the two lines in the same coordinate system: