The quotient of powers with same base
The quotient [[$ \dfrac{4^5}{4^2} $]] is called a quotient of powers with the same base.
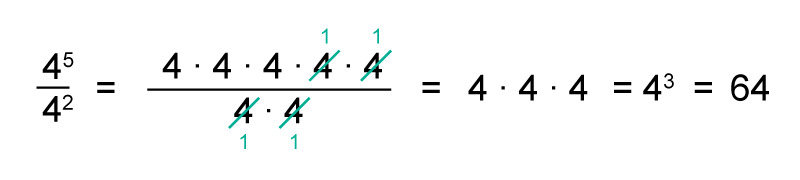
b) [[$ \dfrac{(-4)^7}{(-4)^5} = (-4)^{7-5} = (-4)^2 = 16 $]]
c) [[$ \dfrac{y^7}{y^3} = y^{7-3} = y^4 $]]
d) [[$ \dfrac{a^3 \cdot a^4 \cdot a^6}{a^2 \cdot a^5} = \dfrac{a^{3+4+6}}{a^{2+5}} = \dfrac{a^{13}}{a^7} = a^{13-7} = a^6 $]]
b) [[$ \dfrac{-3^8}{3^5} = -3^{8-5} = -3^3 = -27 $]]
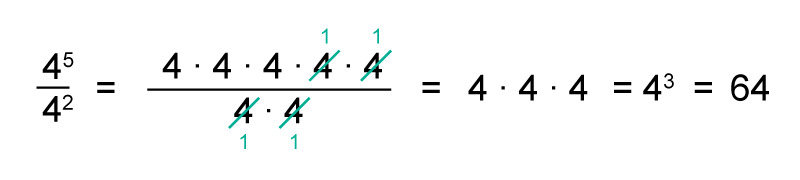
The quotient of powers with the same base
Powers with same base are divided so that the exponent of the denominator is subtracted from the exponent of the numerator. The base number stays the same.
[[$ \dfrac{a^m}{a^n} = a^{m-n}$]]
Example 1
Simplify the powers.
a) [[$ \dfrac{2^6}{2^3} = 2^{6-3} = 2^3 = 8 $]]b) [[$ \dfrac{(-4)^7}{(-4)^5} = (-4)^{7-5} = (-4)^2 = 16 $]]
c) [[$ \dfrac{y^7}{y^3} = y^{7-3} = y^4 $]]
d) [[$ \dfrac{a^3 \cdot a^4 \cdot a^6}{a^2 \cdot a^5} = \dfrac{a^{3+4+6}}{a^{2+5}} = \dfrac{a^{13}}{a^7} = a^{13-7} = a^6 $]]
There are often other factors involved in the quotient of powers with the same base, so you should be careful with the base number.
Example 2
Simplify the powers.
a) [[$ \dfrac{3x^4}{x} = 3x^{4-1} = 3x^3 $]]b) [[$ \dfrac{-3^8}{3^5} = -3^{8-5} = -3^3 = -27 $]]
| c) [[$ \dfrac{6a^4b^2}{3ab} = \dfrac{6}{3}a^{4-1}b^{2-1} = 2a^3b^1 = 2a^3b $]] | Divide the numbers and combine powers with same base. |