Example 1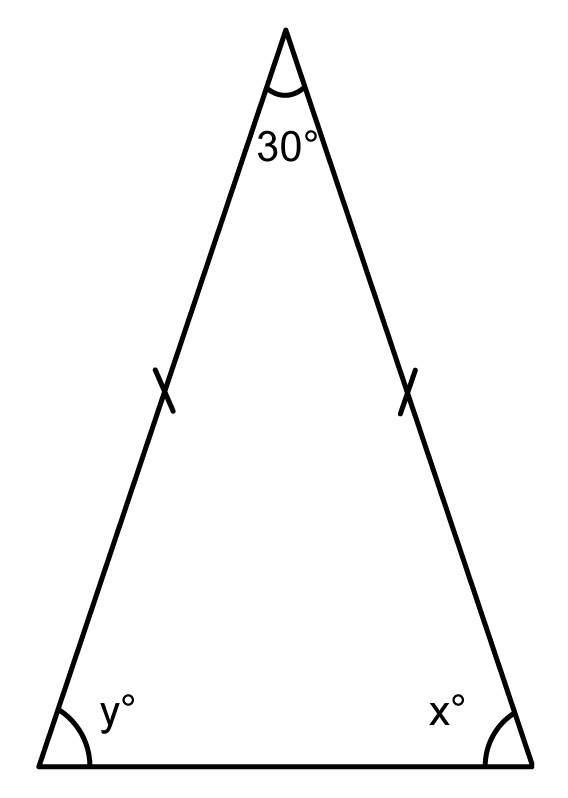

Deduce the magnitudes of angles x and y.

The sum of a triangle's angles is always [[$180°$]], so the sum of the angles x and y is [[$180° - 30° = 150° $]].

Since the triangle is an isosceles triangle , the base angles x and y must be equal. Therefore, the magnitudes of angles x and y are [[$ \dfrac{150°}{2} = 75°$]]

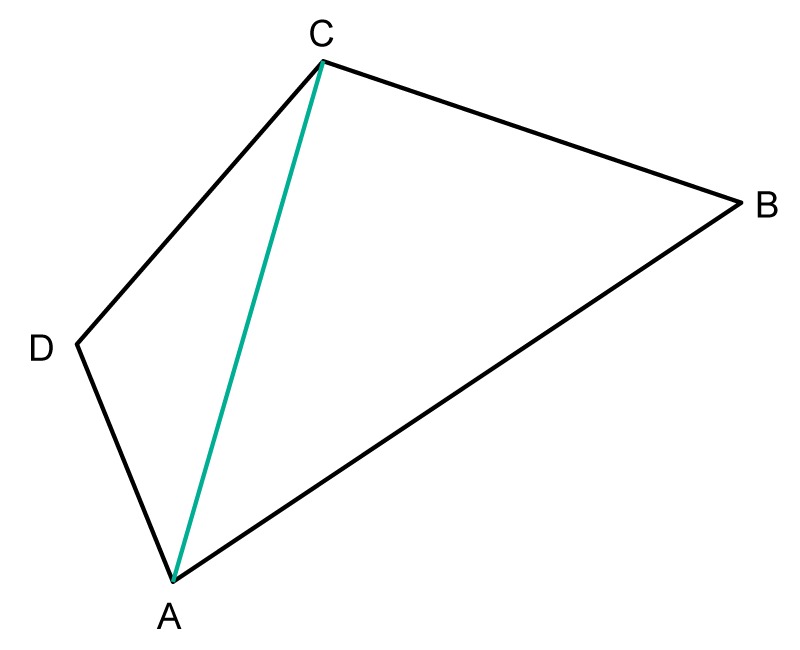
Example 2

Calculate the sum of the angles of the quadrilateral ABCD.

The quadrilateral ABCD can be divided into two triangles, ABC and ACD.

Since the sum of a triangle's angles is [[$180°$]], the sum of the angles of a quadrilateral is [[$ 2 \cdot 180° = 360°$]]. This is true for all quadrilaterals.