3. Angles
Exercises
Basic concepts and theory
An angle is a part of a figure that is bounded by two rays starting from the same point.
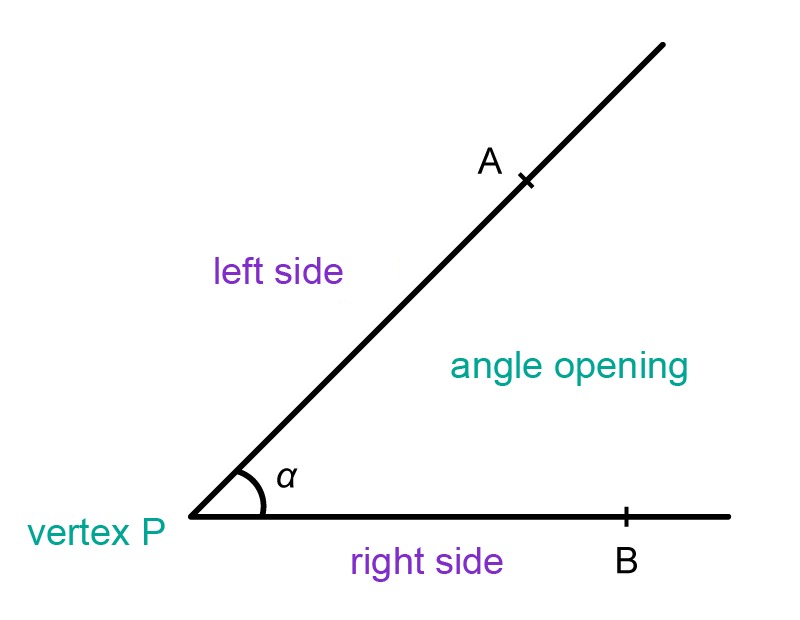
When drawing an angle, the plane is divided into two corners. Unless otherwise stated, the smaller of the resulting corners is usually the angle in question. The corner parts of the angle are the vertex and the rays. When looking to the open part from the tip of the angle, the sides are called the left side and the right side.
Angles are often named with Greek letters [[$ \alpha, \beta, \gamma, \delta, … $]] (read: alpha, beta, gamma, delta). An angle can also be named by its vertex and points selected from its rays (angle APB or [[$ \angle $]] APB), or by the vertex alone (angle P or [[$ \angle $]] P). The magnitude of an angle is measured in degrees.
Types of angles
- Zero angle 0°
- Right angle 90°
- Straight angle 180°
- Full angle 360°
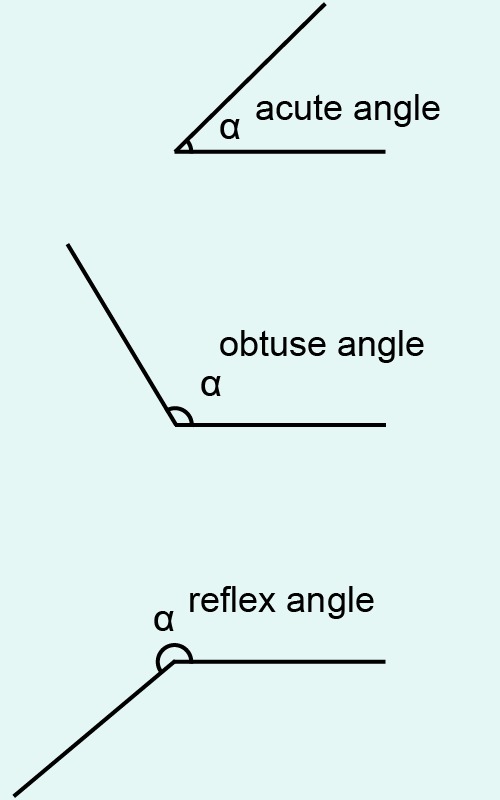
Oblique angles 0° < α < 180°
- acute angles 0° < α < 90°
- obtuse angles 0° < α < 180°
Measuring an angle with a protractor
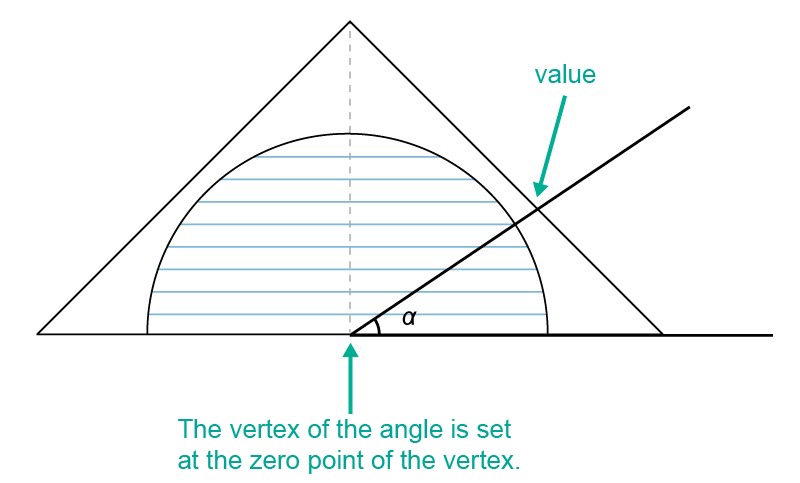 Concave angles can be measured directly with a protractor. The protractor is placed exactly on the angle's vertex, and the degree value is read from where the other side of the angle intersects the protactor. The protractor has two scales, and it is important to choose the correct scale when measuring an angle. The choice of an erroneous scale is avoided by keeping in mind what acute and obtuse angles look like and what their degree values must be.
Concave angles can be measured directly with a protractor. The protractor is placed exactly on the angle's vertex, and the degree value is read from where the other side of the angle intersects the protactor. The protractor has two scales, and it is important to choose the correct scale when measuring an angle. The choice of an erroneous scale is avoided by keeping in mind what acute and obtuse angles look like and what their degree values must be.Example 1
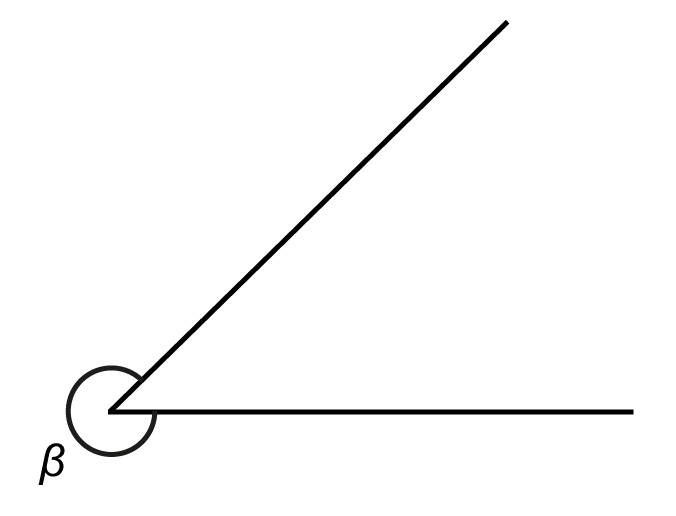
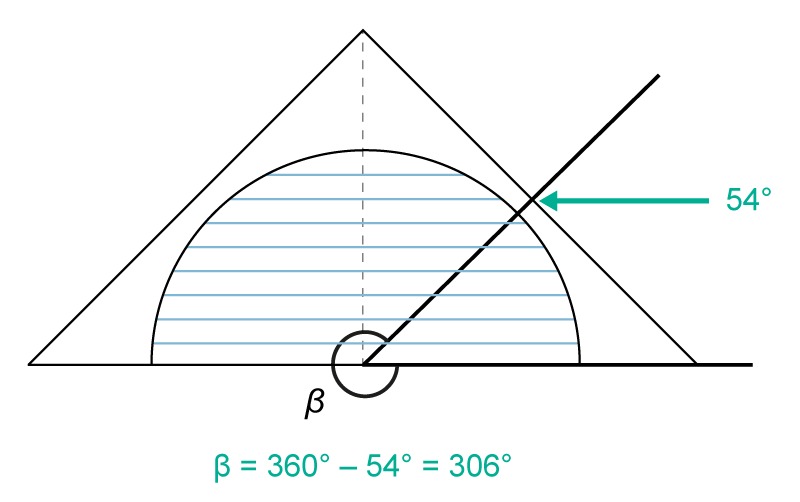
Measure the degree of the angle [[$\beta$]] .This angle is an example of a convex angle, the degree of which cannot be measured directly with a protractor. First, measure the proportion of the acute angle that is missing from the full angle. Subtracting this from 360 ° gives the angle asked.
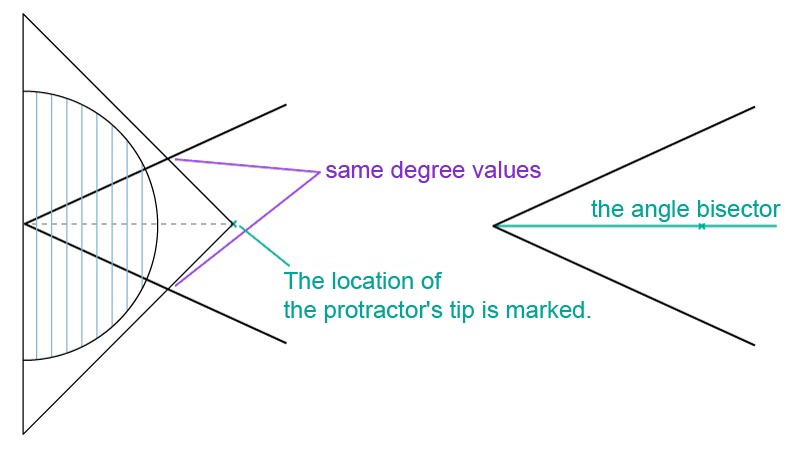
An angle bisectoris a ray that divides the angle into two equal parts.
Bisecting an angle with a protractor
An angle can be bisected with the help of a protractor.