3. Tangent
Tangent
Consider two right triangles, each with an acute angle of [[$ 39,8 ° $]]. The triangles are similar, because the third angles of both triangles are also equal.
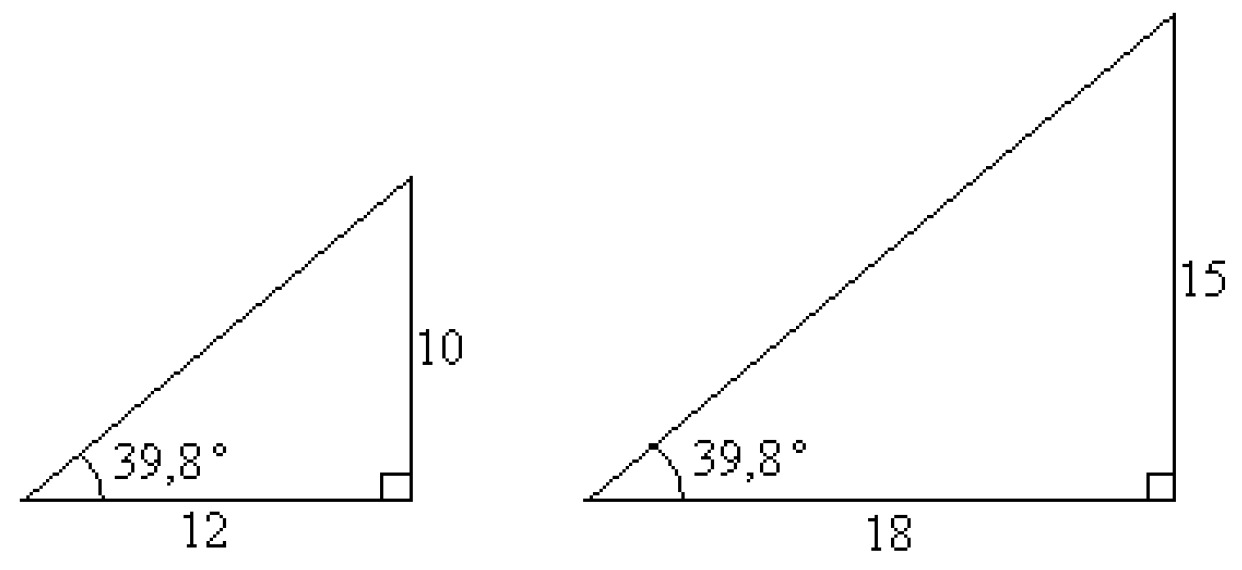
The ratios of the opposite sides of the similar triangles are the same. This means that a comparison can be made:[[$ \displaystyle\frac {12} {18} = \displaystyle\frac {10} {15} $]].
Multiply both sides of the comparison and convert it to another form.
[[$ \begin{align*} \displaystyle\frac {12} {18} &= \displaystyle\frac {10} {15} \;\;\;\;\;\;\;\;\;\;\; {\color {red} {\text {multiply both sides}}} \\ \\ 18 \cdot 10 &= 12 \cdot 15 \;\;\;\;\;\; {\color {blue} {|| :12}} \\ \\ \displaystyle\frac {18 \cdot 10} {12} &= \displaystyle\frac {12 \cdot 15} {12} \;\;\;\;\; {\color {blue} {|| :18}} \;\;\;\; {\color {green} {\text {you can reduce the answer}}} \\ \\ \displaystyle\frac {18 \cdot 10} {18 \cdot 12} &= \displaystyle\frac {15} {18} \\ \\ \displaystyle\frac {10} {12} &= \displaystyle\frac {15} {18} \\ \end{align*} $]]
The comparison expressed in this form means that the ratio between the leg opposite the angle [[$ 39,8 ° $]] and its adjacent leg is constant. The ratios [[$ \displaystyle\frac {10} {12} $]] and [[$ \displaystyle\frac {15} {18} $]] are formed by the lengths of only the sides of one triangle. These ratios are called the tangent of the angle [[$ 39,8 ° $]].
The tangent of a right triangle
In a right triangle, the tangent of the acute angle [[$ \ alpha $]] is the ratio of its opposite leg a to its adjacent leg b.
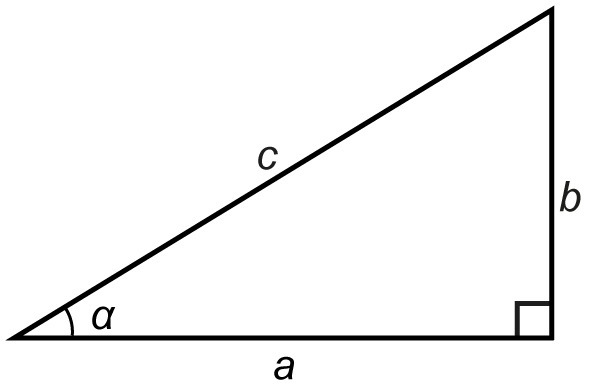
[[$$ \tan \alpha = \displaystyle\frac { \;\alpha\;\text {'s opposite leg}} {\;\alpha\;\text {'s adjacent leg}} = \displaystyle\frac {a} {b} $$]]
Trigonometry is based on the uniformity of right triangles. The values of the trigonometric functions are already tabulated, but they can also be conveniently calculated with function calculators. The tangent of the angle [[$ 39,8 °$]] can be solved by entering the following calculation into a calculator:
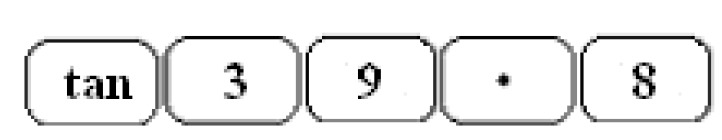 The calculation will give you the result [[$ 0,833 $]], which is the same result as that of the divition [[$ 10: 12 $]] or [[$ 15: 18 $]]. The use of trigonometric functions often facilitates calculations related to rectangular triangles, because the aspect ratios can be immediately exploited when one of the acute corners of the right triangle is known.
The calculation will give you the result [[$ 0,833 $]], which is the same result as that of the divition [[$ 10: 12 $]] or [[$ 15: 18 $]]. The use of trigonometric functions often facilitates calculations related to rectangular triangles, because the aspect ratios can be immediately exploited when one of the acute corners of the right triangle is known.
Similarly, if the lengths of both legs of a right triangle are known, the acute angles of the triangle can be determined by comparing them. The calculator then calculates the inverse of the tangent of the ratio between the lengths of the two legs, which results in the magnitude of the angle in degrees.

Example 1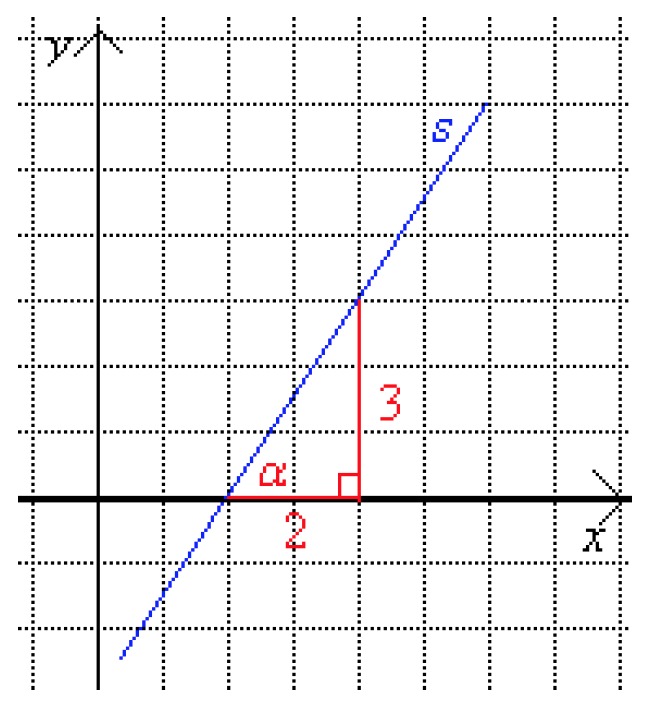
Calculate the angle of the line [[$ s $]] with the [[$ x $]]-axis. This angle is called the line's directional angle.[[$ \begin{align*}
\tan \alpha &= \displaystyle\frac {3} {2} \\
\\
\tan \alpha &= 1,5 \\
\alpha &≈ 56° \\
\end{align*} $]]
The angle [[$ \alpha $]] can be found by calculating the inverse of the tangent with a calculator.
Answer: The magnitude of the angle is 56 °.
Example 2
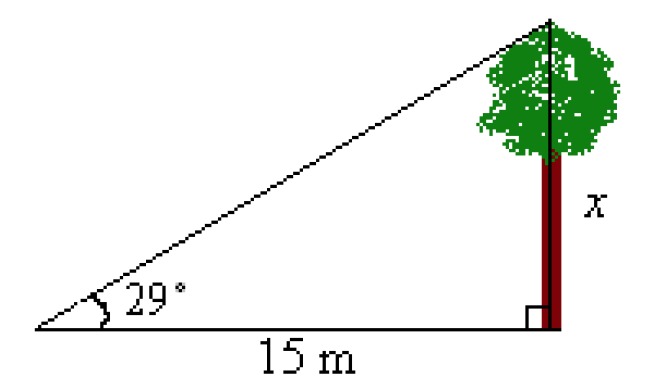
Calculate the height of the tree in the picture.
According to the definition of the tangent, an equation can be written:[[$ \; \tan 29° = \displaystyle\frac {x} {15 \text {m}} $]]
This equation can be solved as follows:
[[$ \begin{align*}
\tan 29° &= \displaystyle\frac {x} {15 \; \text m} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; {\color {blue} {|| \cdot 15 \; \text {m}}} \\
15 \; \text {m} \cdot \tan 29° &= x \\
-x &= -15 \; \text m \cdot \tan 29° \;\;\;\; {\color {blue} {|| \cdot \left (-1\right ) }}\\
x &= 15 \; \text m \cdot \tan 29° \\
x &≈ 8,3 \; \text m \\
\end{align*} $]]
The length of the leg [[$ x $]] can be calculated by entering the following calculation into a calculator:
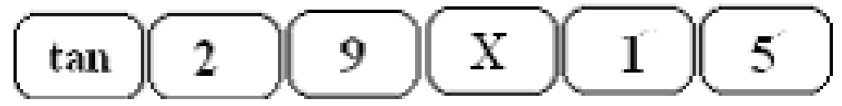
Answer: The height of the tree is [[$ 8,3 $]] m.
Exercises
Basic exercises
Applied exercises
Challenging exercises
2/03. Submission folder for answers
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.