The three squares are formed of similar patterns. Their length ratio is [[$ 1: 2: 3 $]], whereas their area ratio is [[$ 1: 4: 9 $]].

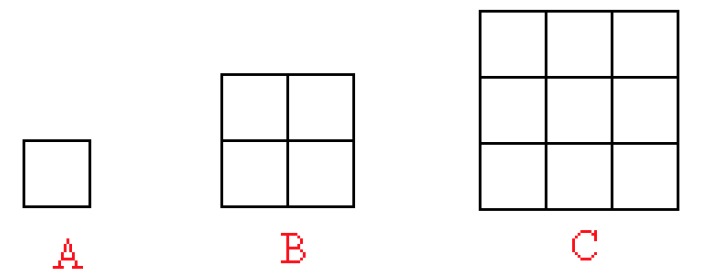
There is a relationship between length and area ratios. Area ratios can be written using length ratios as follows: [[$ 1^2 : 2^2 : 3^2 $]]​.

Similarity in space is defined in the same way as in a plane: two objects are similar if their corresponding lines are proportional. For example, the three cubes below are formed of similar pieces. The ratio of their edge lengths is [[$ 1: 2: 3 $]], whereas their volume ratio is [[$ 1: 8: 27 $]].

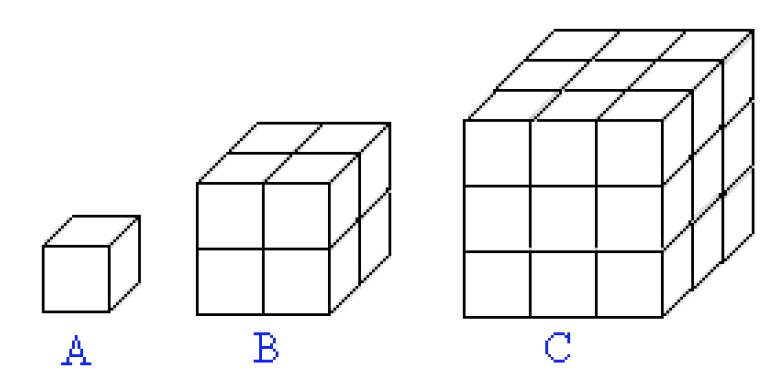
There is also a clear relationship between length and volume ratios. Volume ratios can be written using length ratios as follows: [[$ 1^3 : 2^3 : 3^3 $]]​.

Regular polyhedrons are similar objects. For example, all tetrahedra are similar with each other and all cubes are similar with each other.

Example 1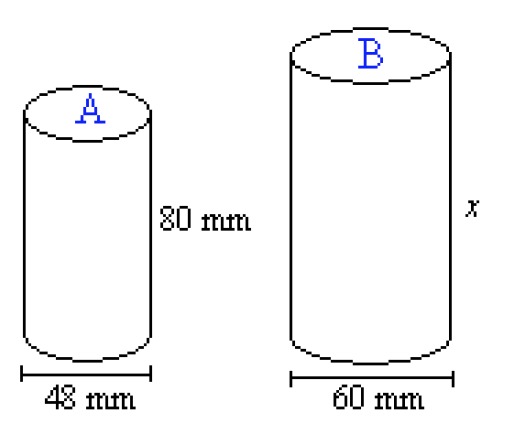

The cylinders [[$ A $]] and [[$ B $]] are similar. Cylinder [[$ A $]] has an area of [[$ 15700\;\text {mm} ^2 $]] and a volume of [[$ 145000 \;\text{mm}^3 $]]​.
Using the data of cylinder [[$ A $]], calculate cylinder [[$ B $]]'s

a) height.

b) area.

c) volume.

Solution:

a) The ratio of the lengths of similar objects is constant.

[[$ \displaystyle\frac {80 \;\text {mm}} {48 \;\text {mm}} = \displaystyle\frac {x} {60 \;\text {mm}} $]],​

and when multiplying both sides we get [[$ x = 100 \;\text {mm} $]]​.

b) The area ratio of similar objects is equal to the square of their length ratios.

[[$ \displaystyle\frac {x} {15700 \;\text {mm}^2} = \left ( \displaystyle\frac {60 \;\text {mm}} {48 \;\text {mm}}\right )^2\;\;\;\; {\color {red} {\text {Select the diameters of the cylinders as the observation lengths.}}} $]]​

Applying general power rules, the following equation is formed:

[[$ \displaystyle\frac {x} {15700 \;\text {mm}^2} = \displaystyle\frac {\left ( 60 \;\text {mm}\right )^2} {\left (48 \;\text {mm}\right )^2} $]]​

By multiplying both sides and using general equation solving rules, we get the result [[$ x = 24500 \;\text {mm}^2 $]]​.

c) The volume ratio of similar objects is equal to the cube of their length ratios.

[[$ \displaystyle\frac {x} {145\;000 \;\text {mm}^3} = \left ( \displaystyle\frac {60 \;\text {mm}} {48 \;\text {mm}}\right )^3 = \displaystyle\frac {\left ( 60 \;\text {mm}\right )^3} {\left (48 \;\text {mm}\right )^3} $]]​

This gives the result [[$ x = 283\;000\;\text{mm}^3 $]]​.

Answer: The height of cylinder [[$ B $]] is [[$ 100 \;\text{cm} $]]​, the area is [[$ 245 \;\text{cm}^2 $]]​ and the volume is [[$ 283 \;\text{cm}^3 $]]​.

Example 2

The right-angled polyhedrons pictured below are similar. The volume of the larger polyhedron is [[$ 36 \;\text{cm}^3 $]]​. What is the volume of the smaller polyhedron?

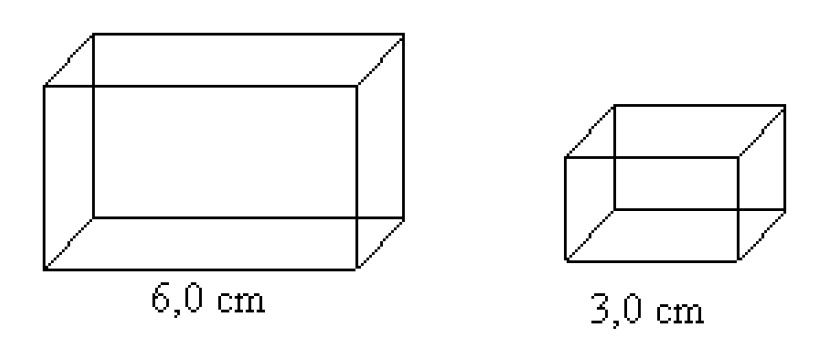
[[$ \begin{align*} \displaystyle\frac {x} {36 \;\text {cm}^3} &= \left ( \displaystyle\frac {3,0 \;\text {cm}} {6,0 \;\text {cm}}\right )^3 \\ \\ \displaystyle\frac {x} {36 \;\text {cm}^3} &= \displaystyle\frac {\left ( 3,0 \;\text {cm}\right )^3} {\left (6,0 \;\text {cm}\right )^3} \\ \\ \displaystyle\frac {x} {36 \;\text {cm}^3} &= \displaystyle\frac {27 \;\text {cm}^3} {216 \;\text {cm}^3} \;\;\;\;\;\;\;\;\;\;\;\;\;\;{\color {red} {\text {multiply both sides}}}\\ \\ 216 \;\text {cm}^3 \cdot x &= 36 \;\text {cm}^3 \cdot 27 \;\text {cm}^3 \;\;\;\;\; {\color {blue} {| \; : 216  \;\text {cm}^3}} \\ \\ x &= \displaystyle\frac {36 \;\text {cm}^3 \cdot 27 \;\text {cm}^3 } {216 \;\text {cm}^3} \\ \\ x &≈ 4,5  \;\text {cm}^3 \end{align*} $]]​

Answer: The volume of the smaller polyhedron is [[$ 4,5 \;\text {cm}^3 $]]​.