Powers and roots
Powers are an abbreviated way of noting multiplication when the same number is multiplied by itself several times.
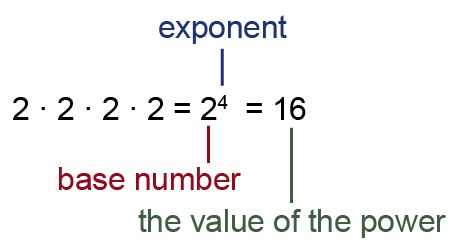
The base number of a power must be accurate. If brackets are not used, the exponent only affects the number directly below the exponent.
If the exponent is zero, the value of the power is always [[$ 1 $]]. However, the base number cannot be zero.
[[$$ a^0 = 1, \;\;\text {when} \;\; a ≠ 0 $$]]
Large and small numbers are usually denoted in a scientific notation form [[$ a \cdot 10^n $]] for the sake of clarity. In a scientific expression, the coefficient [[$ a $]] is always a number between one and ten.
The negative exponent of a power is equal to the corresponding positive power of the inverse of the base number.
[[$$ a ^{-n} = \displaystyle\frac {1} {a^n} \;\;\text{ja}\;\; \left ( \displaystyle\frac {a} {b} \right )^{-n} = \left ( \displaystyle\frac {b} {a} \right )^{n} $$]]If the exponent of a positive base number is a fraction, the same calculation can also be denoted with a root notation.
When [[$ n $]] is a positive integer and [[$ a > 0 $]], [[$ a^{\displaystyle\frac {1} {n}} = \sqrt [n] {a} $]].
The rules for calculating powers can be found in the Tables and formulas section of the book. These are especially needed to simplify power expressions that contain variables. The calculation rules apply to both positive and negative exponents. If the calculation rules are applied when the exponent is a fraction, the base number must be positive.
Example 1
Present the numbers without scientific notation.
a) [[$ 6 \cdot 10^{4} = 60\;000 $]]
b) [[$ 3,2 \cdot 10^{5} = 320\;000 $]]
c) [[$ 9 \cdot 10^{-4} = 0,0004 $]]
d) [[$ 5,8 \cdot 10^{-5} = 0,000058 $]]
Example 2
Simplify using power calculation rules.
a) [[$ 2^0 = 1 $]]b) [[$ 5^3 \cdot 5^4 = 5^{3 + 4} = 5^7 $]]
c) [[$ \displaystyle\frac {6^9} {6^2} = 6^{9 - 2} = 6^7 $]]
d) [[$ \left ( 4^2 \right )^3 = 4^{2 \cdot 3} = 4^6 $]]
Example 3
Simplify the following negative powers.
a) [[$ 2^{-1} = \displaystyle\frac {1} {2^1} = \displaystyle\frac {1} {2} $]]
b) [[$ 5^{-6} = \displaystyle\frac {1} {5^6} $]]
c) [[$ \left ( \displaystyle\frac {3} {4} \right )^{-2} = \left ( \displaystyle\frac {4} {3} \right )^{2} = \displaystyle\frac {16} {9} =1 \displaystyle\frac {7} {9} $]]
Example 4
Simplify the following powers.
a) [[$ 36^{\displaystyle\frac {1} {2}} = \sqrt {36} = 6 $]], because [[$ 6^2 = 36 $]]. "The square root of 36 is 6."
Example 5
Simplify the following root expressions.
a) [[$ \sqrt {90} = \sqrt {9 \cdot 10} = \sqrt {9} \cdot \sqrt {10} = 3\sqrt {10} $]]
b) [[$ \sqrt {20}\sqrt {5} = \sqrt {20 \cdot 5} = \sqrt {100} = 10 $]]
c) [[$ \displaystyle\frac {\sqrt {8}} {\sqrt {2}} = \sqrt {\displaystyle\frac {8} {2}} = \sqrt {4} = 2 $]]