5. Quadratic polynomial functions
Quadratic polynomial functions
A quadratic polynomial function is of the form
[[$ f(x) = ax^2 + bx +c $]],
where [[$ a $]], [[$ b $]] and [[$ c $]] are constants and [[$ a ≠ 0 $]].
The graph of a quadratic polynomial function is a parabola.
Example 1
The simplest quadratic polynomial function is of the form [[$ f (x) = x^2 $]]. Calculate a few points on the curve, place them in the coordinate system, and combine them into a graph. This parabola is called the basic parabola.
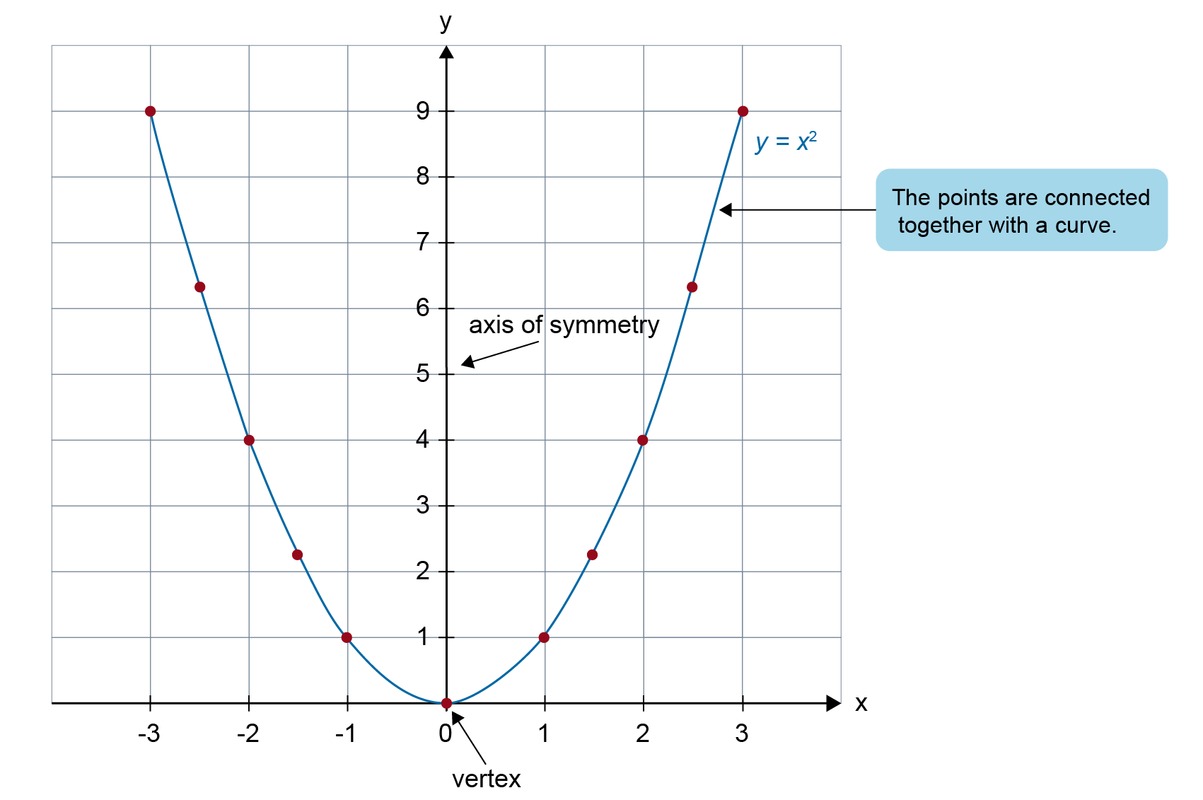
Note! The points of the parabola must not be connected with straight lines. In that case, it would be a piecewise function consisting of many different first-order equations. The graph of a first-order function is always straight, whereas the graphs of higher-order functions are always curvilinear.
The parabola [[$ y = x ^ 2 $]] is symmetric about the [[$ y $]] axis. The point of intersection of the parabola and its axis of symmetry is called the vertex. The points where the graph intersects the [[$ x $]] axis are called the zeros of the parabola.
Example 2
Let us examine the graphs of various functions of the form [[$ f (x) = ax^2 $]]. Draw a few curves in the coordinate system, varying the value of the coefficient [[$ a $]].
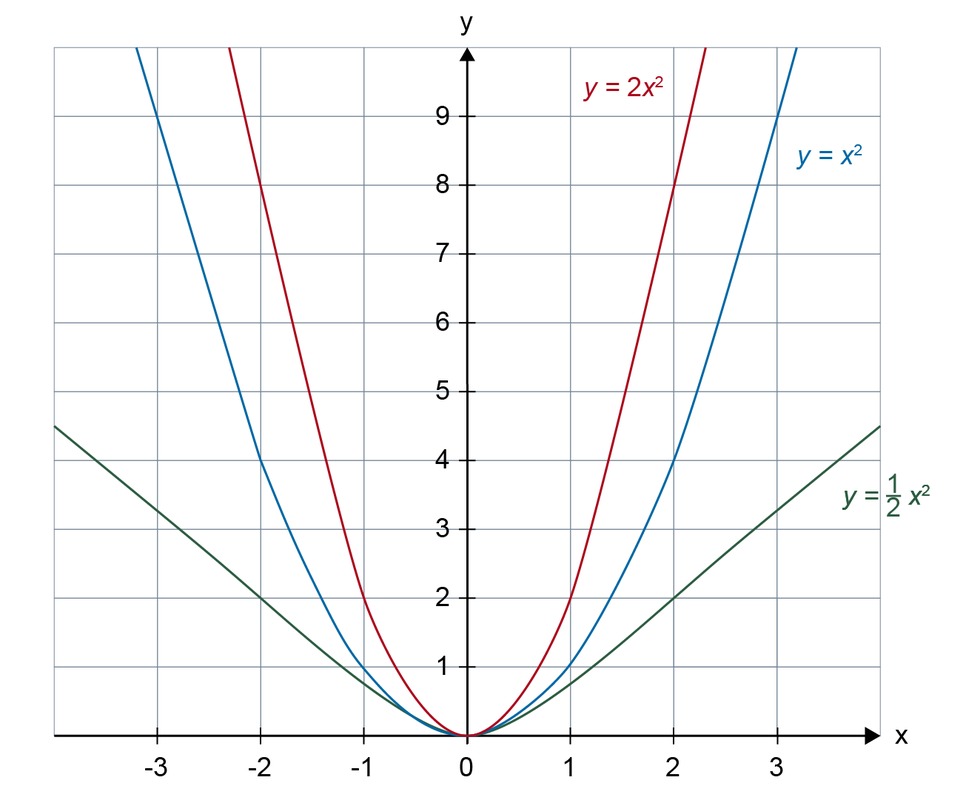
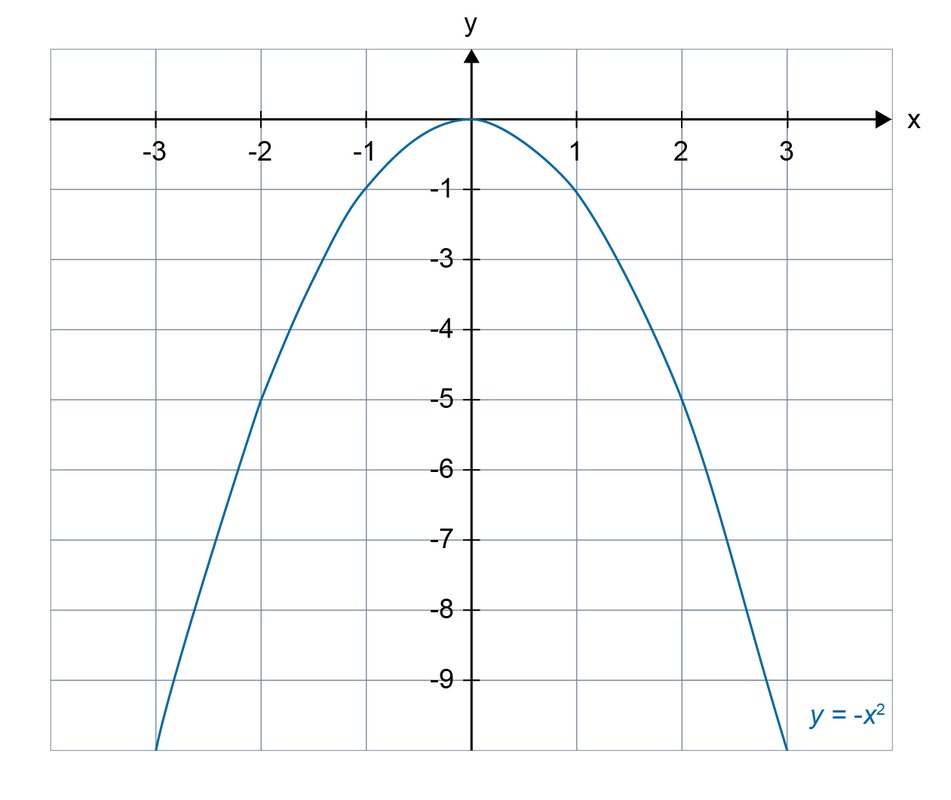
The coefficient of the quadratic variable does not affect the position of the axis of symmetry or the vertex of the curve, but it has a clear effect on the width of the parabola. The graph of the parabola [[$ y = -x^2 $]] is a mirror of the parabola [[$ y = x^2 $]] with respect to the [[$ x $]] axis.
- If [[$ a > 0 $]], the parabola opens upwards.
- If [[$ a < 0 $]], the parabola opens downwards.
- If [[$ |a| $]] is small, the parabola is wide.
- If [[$ |a| $]] is great, the parabola is narrow.
If the graph of a polynomial function is an upward-opening parabola, the function gets its smallest value at the top of the parabola, but the maximum value of the function cannot be determined. Instead, if the graph is a downward-opening parabola, the function gets its maximum value at the top of the parabola, but the minimum value of the function cannot be determined.
Example 3
The minimum value of the functions of the previous example ([[$ f(x) = 2x^2 $]], [[$ f(x) = x^2 $]], [[$ f(x) = \displaystyle\frac {1} {2} x^2 $]]) is [[$ 0 $]], but their maximum value cannot be determined. In contrast, the maximum value of the function [[$ f(x) = -x^2 $]] is [[$ 0 $]], but the minimum value cannot be determined.
Exercises
Basic exercises
Applied exercises
Challenging exercises
3/05. Submission folder for answers
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.