12. Direct and inverse proportionality

Direct and inverse proportionality

Proportionalities can be used to solve various kinds of problems. Before forming a relationship between two quantities, it must be concluded whether there is direct or inverse proportionality between them. Directly proportional quantities change in the same proportion and can be illustrated by a line passing through the origin.

If the quantities [[$ x $]] and [[$ y $]] are directly proportional, their number pairs [[$ (x_1, y_1) $]] and [[$ (x_2, y_2) $]] carry out the comparison [[$ \displaystyle\frac {y_1} {x_1} = \displaystyle\frac {y_2} {x_2} $]].

This can also be written in the form [[$ \displaystyle\frac {y_1} {y_2} = \displaystyle\frac {x_1} {x_2} $]]

Inversely proportional quantities change so that as one quantity grows, the other one decreases. However, the product of the variables always remains the same.

If the quantities [[$ x $]] and [[$ y $]] are inversely proportional, their number pairs [[$ (x_1, y_1) $]] and [[$ (x_2, y_2) $]] carry out the comparison [[$ x_1y_1 = x_2y_2 $]].

This can also be written in the form [[$ \displaystyle\frac {x_1} {x_2} = \displaystyle\frac {y_2} {y_1} $]]

Example 1

Susanne spent [[$ 12 $]] minutes rollerblading a distance of five kilometers. How long would it take for her to skate [[$ 23 \; \text {km} $]]? Suppose that Susanne skates at a constant, stable speed.

Solution:

A model can be used to help create a comparison. Mark the requested time with [[$ x $]] and determine whether the time spent increases or decreases as the distance increases.

Since the arrows are parallel, the qualities are directly proportional. When the comparison is made, the arrows on both sides of the equation must be parallel.

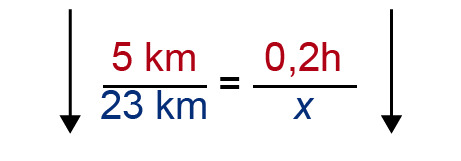
Solve the equation by first performing the multiplication.

[[$ \begin{align*} 5 \;\text{km} \cdot x &= 23 \;\text{km} \cdot 0,2 \;\text{h} \;\;\;\; || : 5 \;\text{km} \\ x &= \displaystyle\frac {23 \;\text{km} \cdot 0,2 \;\text{h}} {5 \;\text{km}} \\ x &= 0,92 \;\text{h} \\ x &≈ 55 \;\text{min} \end{align*} $]]

Answer: Susanne skates [[$ 23 \;\text{km} $]] in [[$ 55 $]] minutes.

Example 2

If Susanne skates at a speed of [[$ 20 \;\text{km/h} $]], the journey from home to her grandmother's house takes [[$ 45 \;\text {min} $]]. How much time would be saved if her speed was [[$ 25 \;\text{km/h} $]]?

Solution:

Let's start by solving how long it takes to travel at the speed of [[$ 25 \;\text{km/h} $]]. Mark the travel time with [[$ x $]] and create a set of speeds and times. The higher the speed, the less time it takes to travel the same length. The same units must be used for calculations, so the time is converted to hours.

Since the arrows point in different directions, the quantities are inversely proportional. In order to make a comparison between the two quantities, the direction of one of the arrows must be changed.

Solve the equation by first performing the multiplication.

[[$ \begin{align*} 25 \;\text{km/h} \cdot x &= 20 \;\text{km/h} \cdot 0,75 \;\text{h} \;\;\;\; || : 25 \;\text{km/h} \\ x &= \displaystyle\frac {20 \;\text{km/h} \cdot 0,75 \;\text{h}} {25 \;\text{km/h}} \\ x &= 0,6 \;\text{h} \\ x &≈ 36 \;\text{min} \\ \end{align*} $]]

The difference between the times is [[$ 45 \;\text {min} - 36 \;\text {min} = 9 \;\text {min} $]].

Answer: The trip takes [[$ 9 $]] minutes less when traveling at a speed of [[$ 25 \;\text {km/h} $]].