1.2. Tilastollisia tunnuslukuja
.
1.2. tilastollisia tunnuslukuja
Sähköisten työvälineiden käyttöohjeet löydät vasemmalta.

Luokitellun aineiston tunnusluvut GeoGebralla
Geogebran käyttö LUMA
Luokiteltu aineisto LUMA
- jos luokiteltava aineisto on jatkuva, ota luokan todelliset ylä- ja alarajat tarkempana kuin tehtävässä annetut arvot. Esim. aika, pituus
- jos luokiteltava aineisto on diskreetti, ota rajat kokonaislukuna.
- jos luokiteltavan aineiston alarajana on nolla (0) mieti voiko todellinen alaraja olla negatiivinen vai ei.
vaihteluvälin pituus = suurin havaintoarvo – pienin havaintoarvo
keskiarvo
keskihajonta
Luokiteltu aineisto
[[$ \bar{x}=\dfrac{\sum\limits_{i=1}^{k}{{{f}_{i}}{{x}_{i}}}}{\sum\limits_{i=1}^{k}{{{f}_{i}}}} $]]
keskiarvo
x= arvo
f= esiintymiskertojen lukumäärä (=frekvenssi)
n=esiintymiskerrat
∑ =summan merkki
keskihajonta
Diskreetin aineiston [[$ \color{green}{luokkien \ luokkakeskusten} $]] määrittäminen:
Esimerkki 1.
Kuusi henkilöä arvioi elokuvan asteikolla 0–5 pistettä. Arviot olivat 5, 0, 2, 5, 1 ja 5. Määritä elokuvan saamien arvioiden
a) moodi
b) keskiarvo
c) mediaani
d) keskihajonta.

Laskut tulee osata tehdä itse A-osassa!
B-osassa voit käyttää apunasi sähköisiä työvälineitä.
E1. Tilastollisia tunnuslukuja GG6:lla
Esimerkki luokitellun aineiston tutkimisesta:
Esimerkki 2
https://vimeo.com/user44764609/review/273292817/5f8bcbbe41
Luokitellun aineiston todelliset rajat ja luokkakeskukset
Keskiluvut LibreOffice Calcilla
Ratkaisut:
Kopioi taulukko LibreOffice Calkiin
Ota seuraavat kuvakaappaukset ratkaisuusi. Ovat perustelu vastauksellesi!

tai esitä laskuna:
Muista laskujen kaavat löytyvät MAOLsta, kannattaa aina tarkistaa ne sieltä. MAOLsta löytyy myös selitykset termeille.



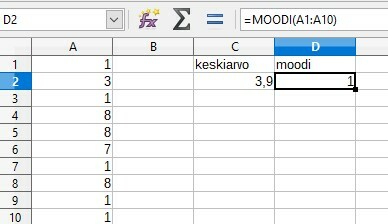
tai esitä laskuna
kirjoita arvot suuruusjärjestyksessä 1111137888
kirjoita esiintymiskerrat taulukkoon

tai esitä laskuna
Kirjoita taulukon luvut suuruusjärjestykseen, huomioi myös jokaisen luvun esiintymiskerrat:
1111 13 7888 kahden keskimmäisen luvun 1 ja 3 keskiarvo on Md=2
Md=2
V:


Ota seuraavat kuvakaappaukset ratkaisuusi. Ovat perustelu vastauksellesi!

tai esitä laskuna:
Muista laskujen kaavat löytyvät MAOLsta, kannattaa aina tarkistaa ne sieltä. MAOLsta löytyy myös selitykset termeille.

tai esitä laskuna
kirjoita arvot suuruusjärjestyksessä 1111137888
kirjoita esiintymiskerrat taulukkoon
| luku | f, esiintymiskertojen lukumäärä(kpl) | |
| 1 | 5 | Mo=1, sillä se esiintyy useimmin, f=5 kpl |
| 3 | 1 | |
| 7 | 1 | |
| 8 | 3 | |
| yhteensä | taulukossa on yhteensä 5+1+1+3= 10 lukua |

tai esitä laskuna
Kirjoita taulukon luvut suuruusjärjestykseen, huomioi myös jokaisen luvun esiintymiskerrat:
1111 13 7888 kahden keskimmäisen luvun 1 ja 3 keskiarvo on
V:
Regressiosuora
Kahden muuttujan välillä on lineaarinen riippuvuus, jos niiden välinen yhteys voidaan kuvata suoralla tai sen osalla.
Lineaarisen riippuvuuden voimakkuuden tunnuslukuna käytetään korrelaatiokerrointa r, jonka arvo on välillä [-1,1]
Kuva 1. Kuva 2.


Kuva 3.

 , joka kuvaa kuinka monta prosenttia toisistaan riippuvat tilastomuuttujat selittävät toistensa vaihtelusta. (Kertaa MAB5 kurssista)
, joka kuvaa kuinka monta prosenttia toisistaan riippuvat tilastomuuttujat selittävät toistensa vaihtelusta. (Kertaa MAB5 kurssista)
Korrelaation määrittäminen(MAB5) r
Selitysasteen määrittäminen(MAB5) R2
Esimerkki 3.



Ohjeet tehtävän ratkaisuun:
Siirrä aineisto GeoGebra 6:n taulukkolaskentaan.


Muodosta lineaalinen malli Asunnon koon ja hinnan välille

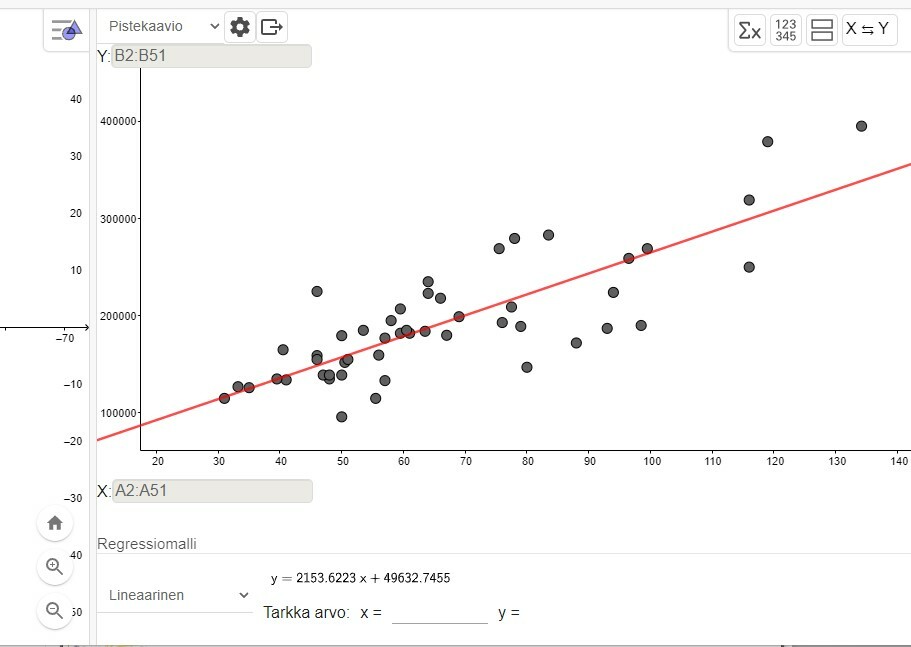

Vastauksena esimerkin kysymyksiin sinun tulee liittää kuvakaappaus ja kertoa sen perusteellla vastauksesi:
a)

a) Asuntojen korrelaatiokerroin on r= 0,8157 eli noi 0,82. Asunnon kokojen ja hintojen välillä on voimakas positiivinen korrelaatio.
Selitys aste r2 = 0,6654 eli noin 0,67 . Asunnon pinta-ala selittää noin 67% asunnon hinnan vaihtelusta.
b) Regressiosuoran yhtälö on y = 2153,62x + 49632,75

V: Regressiosuoran avulla, kun asunnon koko on 30 m2 saadaan asunnon hinnaksi noin 114 000 euroa.
c)
y=100 000
Ratkaistu CAS-lasmimella

V: Asunnon jonka koko on noin 23 m2 saa 100 000 euroa
Lineaarisen riippuvuuden voimakkuuden tunnuslukuna käytetään korrelaatiokerrointa r, jonka arvo on välillä [-1,1]
- Kun
on kyseessä voimakas positiininen korrelaatio, eli pisteet menevät lähelle samaa nousevaa suoraa (kuva 1)
- Kun
on kyseessä voimakas negatiivinen korrelaatio, eli pisteet menevät lähelle samaa laskevaa suoraa (kuva 2)
- Kun
ei korrelaatiota ole (kuva 3)
Kuva 1. Kuva 2.


Kuva 3.

Korrelaation määrittäminen(MAB5) r
Selitysasteen määrittäminen(MAB5) R2
Esimerkki 3.



Ohjeet tehtävän ratkaisuun:
Siirrä aineisto GeoGebra 6:n taulukkolaskentaan.


Muodosta lineaalinen malli Asunnon koon ja hinnan välille



Vastauksena esimerkin kysymyksiin sinun tulee liittää kuvakaappaus ja kertoa sen perusteellla vastauksesi:
a)

a) Asuntojen korrelaatiokerroin on r= 0,8157 eli noi 0,82. Asunnon kokojen ja hintojen välillä on voimakas positiivinen korrelaatio.
Selitys aste r2 = 0,6654 eli noin 0,67 . Asunnon pinta-ala selittää noin 67% asunnon hinnan vaihtelusta.
b) Regressiosuoran yhtälö on y = 2153,62x + 49632,75

V: Regressiosuoran avulla, kun asunnon koko on 30 m2 saadaan asunnon hinnaksi noin 114 000 euroa.
c)
y=100 000
Ratkaistu CAS-lasmimella

V: Asunnon jonka koko on noin 23 m2 saa 100 000 euroa

