Regressiosuora
Kahden muuttujan välillä on lineaarinen riippuvuus, jos niiden välinen yhteys voidaan kuvata suoralla tai sen osalla.
Lineaarisen riippuvuuden voimakkuuden tunnuslukuna käytetään korrelaatiokerrointa r, jonka arvo on välillä [-1,1]
Kuva 1. Kuva 2.
Kuva 3.
, joka kuvaa kuinka monta prosenttia toisistaan riippuvat tilastomuuttujat selittävät toistensa vaihtelusta. (Kertaa MAB5 kurssista)
Korrelaation määrittäminen(MAB5) r
Selitysasteen määrittäminen(MAB5) R2
Esimerkki 3.
Ohjeet tehtävän ratkaisuun:
Siirrä aineisto GeoGebra 6:n taulukkolaskentaan.
Muodosta lineaalinen malli Asunnon koon ja hinnan välille
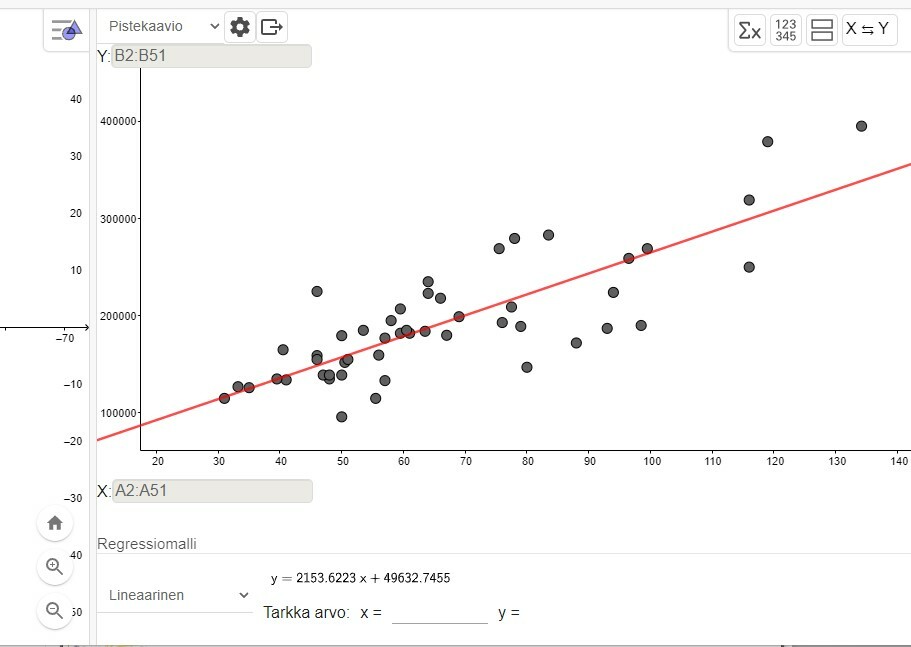
Vastauksena esimerkin kysymyksiin sinun tulee liittää kuvakaappaus ja kertoa sen perusteellla vastauksesi:
a)
a) Asuntojen korrelaatiokerroin on r= 0,8157 eli noi 0,82. Asunnon kokojen ja hintojen välillä on voimakas positiivinen korrelaatio.
Selitys aste r2 = 0,6654 eli noin 0,67 . Asunnon pinta-ala selittää noin 67% asunnon hinnan vaihtelusta.
b) Regressiosuoran yhtälö on y = 2153,62x + 49632,75
V: Regressiosuoran avulla, kun asunnon koko on 30 m2 saadaan asunnon hinnaksi noin 114 000 euroa.
c)
y=100 000
Ratkaistu CAS-lasmimella
V: Asunnon jonka koko on noin 23 m2 saa 100 000 euroa
Lineaarisen riippuvuuden voimakkuuden tunnuslukuna käytetään korrelaatiokerrointa r, jonka arvo on välillä [-1,1]
- Kun
on kyseessä voimakas positiininen korrelaatio, eli pisteet menevät lähelle samaa nousevaa suoraa (kuva 1) - Kun
on kyseessä voimakas negatiivinen korrelaatio, eli pisteet menevät lähelle samaa laskevaa suoraa (kuva 2) - Kun
ei korrelaatiota ole (kuva 3)
Kuva 1. Kuva 2.
Kuva 3.
, joka kuvaa kuinka monta prosenttia toisistaan riippuvat tilastomuuttujat selittävät toistensa vaihtelusta. (Kertaa MAB5 kurssista)Korrelaation määrittäminen(MAB5) r
Selitysasteen määrittäminen(MAB5) R2
Esimerkki 3.
Ohjeet tehtävän ratkaisuun:
Siirrä aineisto GeoGebra 6:n taulukkolaskentaan.
Muodosta lineaalinen malli Asunnon koon ja hinnan välille
Vastauksena esimerkin kysymyksiin sinun tulee liittää kuvakaappaus ja kertoa sen perusteellla vastauksesi:
a)
a) Asuntojen korrelaatiokerroin on r= 0,8157 eli noi 0,82. Asunnon kokojen ja hintojen välillä on voimakas positiivinen korrelaatio.
Selitys aste r2 = 0,6654 eli noin 0,67 . Asunnon pinta-ala selittää noin 67% asunnon hinnan vaihtelusta.
b) Regressiosuoran yhtälö on y = 2153,62x + 49632,75
V: Regressiosuoran avulla, kun asunnon koko on 30 m2 saadaan asunnon hinnaksi noin 114 000 euroa.
c)
y=100 000
Ratkaistu CAS-lasmimella
V: Asunnon jonka koko on noin 23 m2 saa 100 000 euroa