Ratkaisu esimerkki 2
a) Alla aika-nopeus -kuvaaja esitettynä graafisesti.
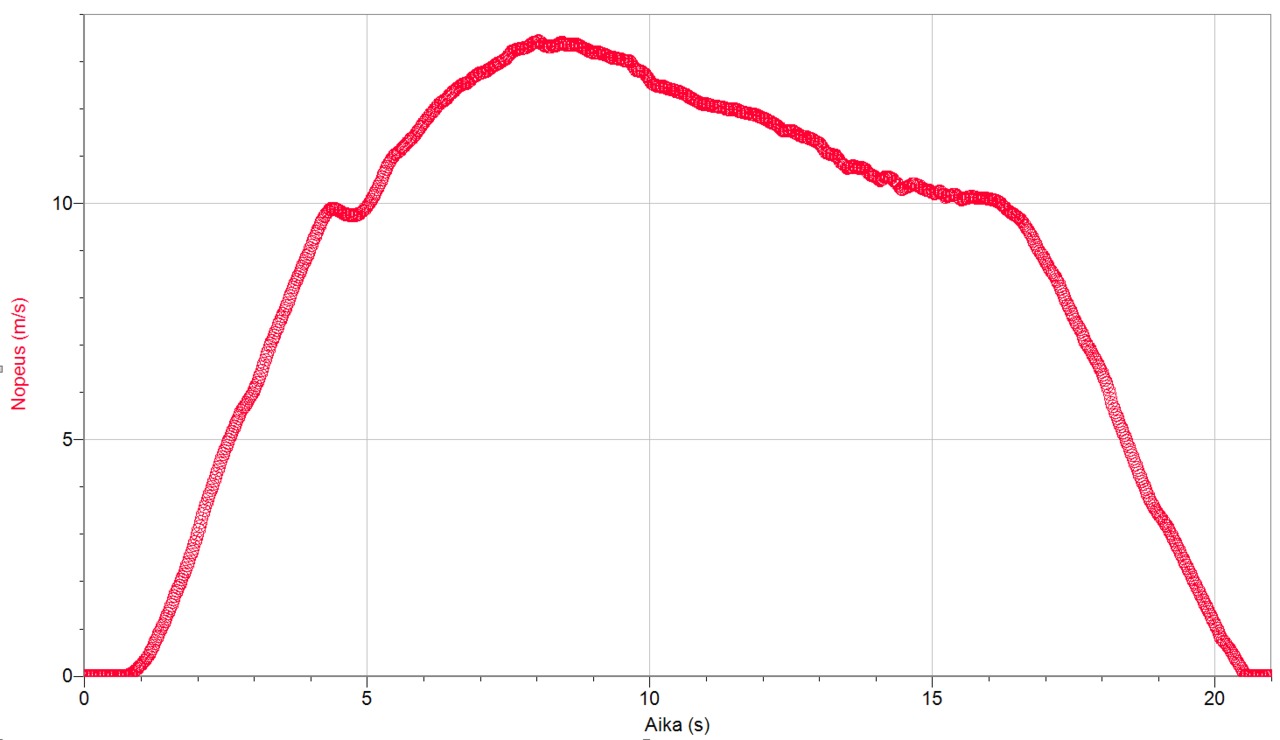
b) Kuvaajalta voidaan löytää suurin nopeus 13,43 m/s kohdasta 8,04 s. Kuvaaja alla.

Kysytyssä yksikössä tämä on
[[$ 13,43 \text{ m/s}=13,43 \cdot 3,6 \text{ km/h}\approx 48 \text{ km/h} $]]
c) Kiihtyvyys on nopeuden kuvaajan derivaatta. Mittausohjelmistolla voidaan määrittää derivaatan eli tangentin kulmakertoimen arvoja eri kohdissa. Suurin arvo on noin 3,7 m/s2 kohdassa 3,2 s. Kuva alla.

d) Kuljettu matka on kuvaajan integraali eli kuvaajan ja x-akselin välinen pinta-ala. Mittausohjelmistolla saadaan määritettyä matkaksi
[[$ s=177,9 \text{ m}\approx 180\text{ m} $]]
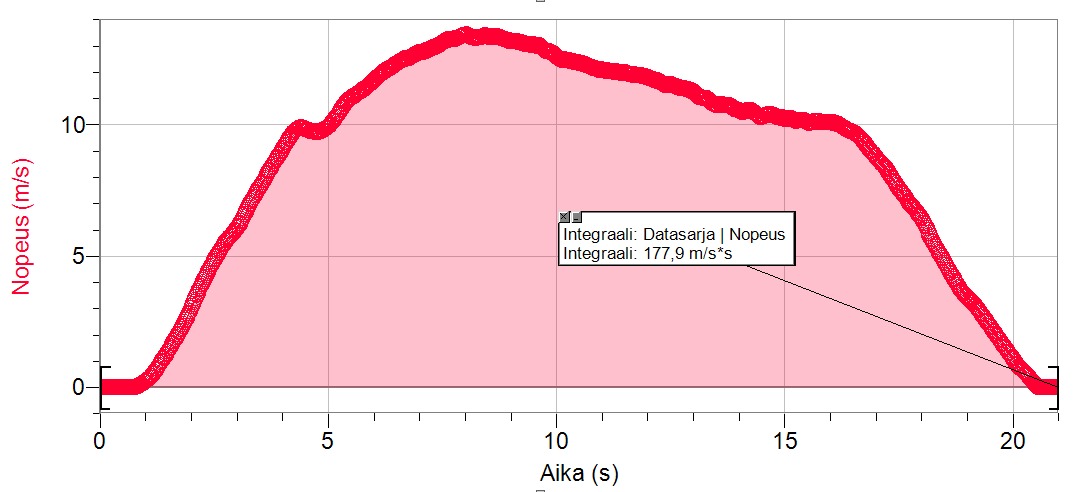
e) Keskinopeus on siirtymä jaettuna ajalla. Siirtymä on yhtä suuri kuin matka, sillä liike etenee koko ajan samaan suuntaan. Koko mittauksen kesto on 21 s.
[[$ v_k=\dfrac{\Delta x}{\Delta t}=\dfrac{177,9\text{ m}}{21 \text{ s}}\approx 8,5 \text{ m/s} $]]

b) Kuvaajalta voidaan löytää suurin nopeus 13,43 m/s kohdasta 8,04 s. Kuvaaja alla.

Kysytyssä yksikössä tämä on
[[$ 13,43 \text{ m/s}=13,43 \cdot 3,6 \text{ km/h}\approx 48 \text{ km/h} $]]
c) Kiihtyvyys on nopeuden kuvaajan derivaatta. Mittausohjelmistolla voidaan määrittää derivaatan eli tangentin kulmakertoimen arvoja eri kohdissa. Suurin arvo on noin 3,7 m/s2 kohdassa 3,2 s. Kuva alla.

d) Kuljettu matka on kuvaajan integraali eli kuvaajan ja x-akselin välinen pinta-ala. Mittausohjelmistolla saadaan määritettyä matkaksi
[[$ s=177,9 \text{ m}\approx 180\text{ m} $]]

e) Keskinopeus on siirtymä jaettuna ajalla. Siirtymä on yhtä suuri kuin matka, sillä liike etenee koko ajan samaan suuntaan. Koko mittauksen kesto on 21 s.
[[$ v_k=\dfrac{\Delta x}{\Delta t}=\dfrac{177,9\text{ m}}{21 \text{ s}}\approx 8,5 \text{ m/s} $]]