Graafisten esimerkkien ratkaisut
Esimerkki 1 malliratkaisu
Kommentti: Tiheyden määritelmä on [[$ \rho=m/V $]]. Tämän voi ilmaista myös muodossa [[$ m=\rho V $]]. Tiheys on siis suoran kulmakerroin kun massa esitetään tilavuuden funktiona (Kuten suoran yhtälö y=kx matematiikassa). Kirjataan tulokset Loggerpro:n sarakkeisiin. Nimetään sarakkeet ja niiden yksiköt sarakkeen ominaisuuksista. Tehdään lineaarinen sovitus ja otetaan kuvaajasta kuvankaappaus, jossa sovitus näkyy parametreineen.
a) Määritelmän [[$ \rho=m/V $]] nojalla tiheys on tilavuus-massa -kuvaajan fysikaalinen kulmakerroin. Alla olevan suoran sovituksen mukaan tiheys on 0,87 g/ml.
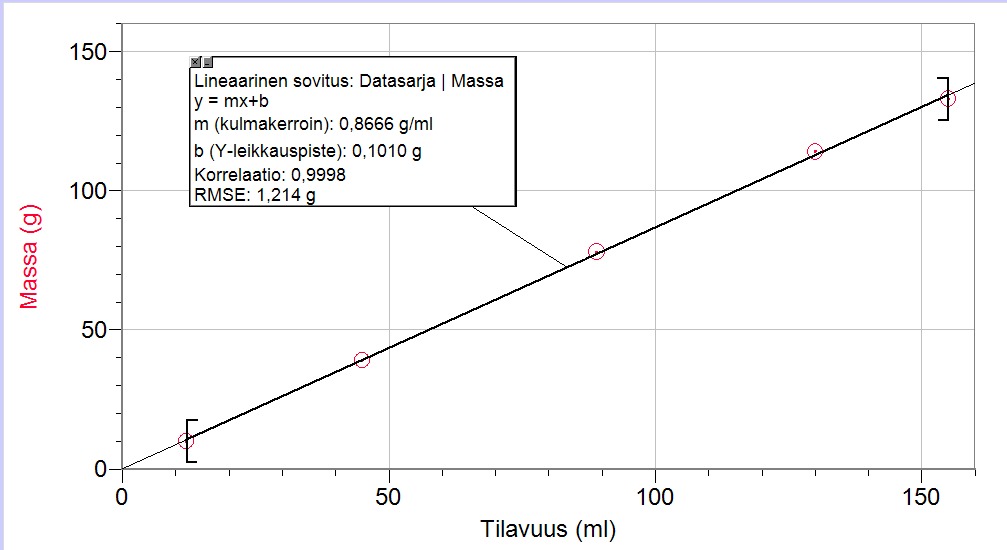
Kommentti: Perustellaan ja ilmoitetaan vastaus yksiköineen ja pyöristettynä sopivaan tarkkuuteen. Sopiva tarkkuus riippuu mittaustulosten ja suoran sovituksen tarkkuudesta. 2 numeron tarkkuus on graafisissa tehtävissä tavanomainen.
b) Kuvaajasta voidaan lukea massan arvo kohdassa, jossa tilavuus on 0,85 litraa eli 850 ml. Alla olevan kuvaajan mukaisesti kysytty massa on 740 g.
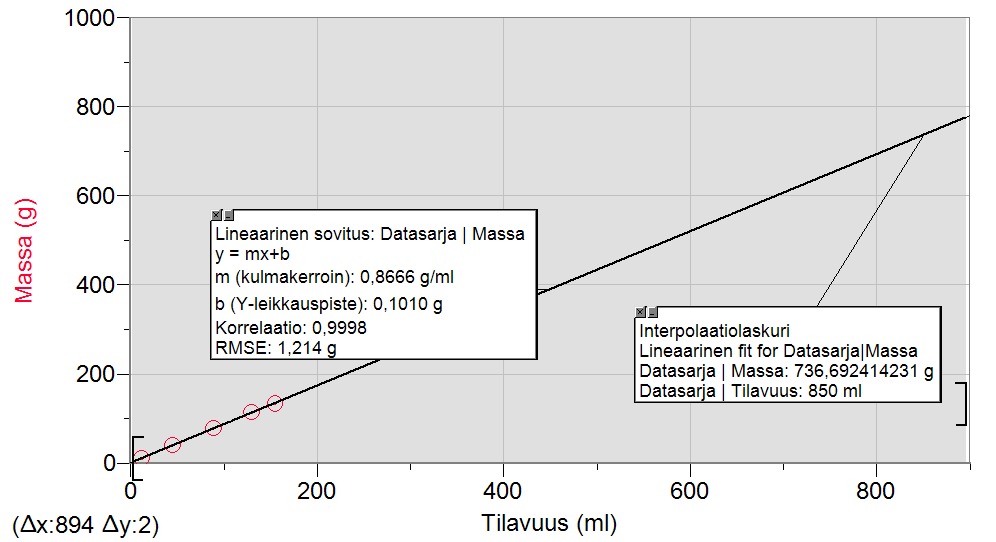
Kommentti: Tilavuuden määritys pitää perustelella tekemällä merkintä kuvaajaan ja liittämällä uusi kuvankaappaus. Pelkästä lukuarvon maininnasta ei saa pisteitä vaikka arvo olisi oikein. Merkintä onnistuu Loggerpron "interpolaatiolaskuri"-työkalulla, mutta laskuria varten akseleita sekä lineaarisen sovituksen maalattua aluetta tulee skaalata niin, että kysytty kohta on näkyvissä. Kuvaajaa voi skaalata klikkaamalla akselin suurinta lukuarvoa.
a) Määritelmän [[$ \rho=m/V $]] nojalla tiheys on tilavuus-massa -kuvaajan fysikaalinen kulmakerroin. Alla olevan suoran sovituksen mukaan tiheys on 0,87 g/ml.

Kommentti: Perustellaan ja ilmoitetaan vastaus yksiköineen ja pyöristettynä sopivaan tarkkuuteen. Sopiva tarkkuus riippuu mittaustulosten ja suoran sovituksen tarkkuudesta. 2 numeron tarkkuus on graafisissa tehtävissä tavanomainen.
b) Kuvaajasta voidaan lukea massan arvo kohdassa, jossa tilavuus on 0,85 litraa eli 850 ml. Alla olevan kuvaajan mukaisesti kysytty massa on 740 g.

Kommentti: Tilavuuden määritys pitää perustelella tekemällä merkintä kuvaajaan ja liittämällä uusi kuvankaappaus. Pelkästä lukuarvon maininnasta ei saa pisteitä vaikka arvo olisi oikein. Merkintä onnistuu Loggerpron "interpolaatiolaskuri"-työkalulla, mutta laskuria varten akseleita sekä lineaarisen sovituksen maalattua aluetta tulee skaalata niin, että kysytty kohta on näkyvissä. Kuvaajaa voi skaalata klikkaamalla akselin suurinta lukuarvoa.
Ratkaisu esimerkki 2
a) Alla aika-nopeus -kuvaaja esitettynä graafisesti.
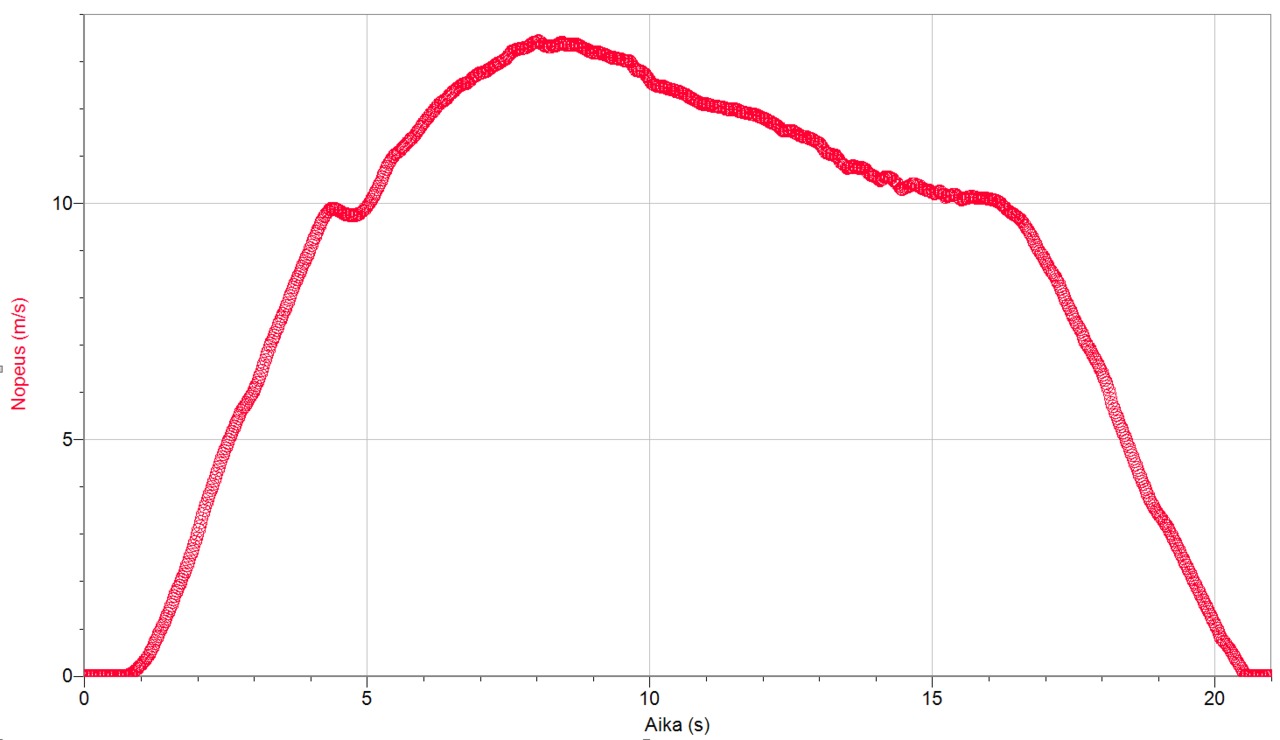
b) Kuvaajalta voidaan löytää suurin nopeus 13,43 m/s kohdasta 8,04 s. Kuvaaja alla.

Kysytyssä yksikössä tämä on
[[$ 13,43 \text{ m/s}=13,43 \cdot 3,6 \text{ km/h}\approx 48 \text{ km/h} $]]
c) Kiihtyvyys on nopeuden kuvaajan derivaatta. Mittausohjelmistolla voidaan määrittää derivaatan eli tangentin kulmakertoimen arvoja eri kohdissa. Suurin arvo on noin 3,7 m/s2 kohdassa 3,2 s. Kuva alla.

d) Kuljettu matka on kuvaajan integraali eli kuvaajan ja x-akselin välinen pinta-ala. Mittausohjelmistolla saadaan määritettyä matkaksi
[[$ s=177,9 \text{ m}\approx 180\text{ m} $]]
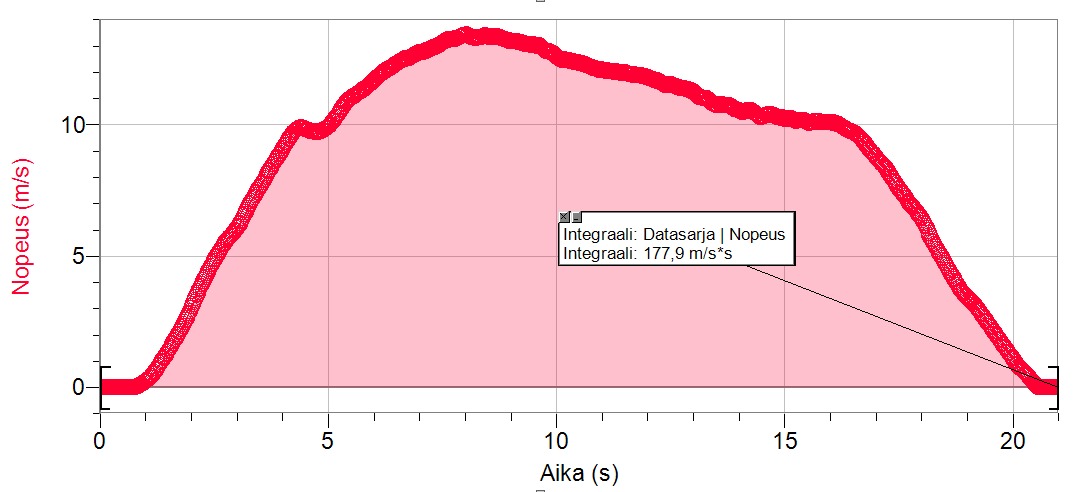
e) Keskinopeus on siirtymä jaettuna ajalla. Siirtymä on yhtä suuri kuin matka, sillä liike etenee koko ajan samaan suuntaan. Koko mittauksen kesto on 21 s.
[[$ v_k=\dfrac{\Delta x}{\Delta t}=\dfrac{177,9\text{ m}}{21 \text{ s}}\approx 8,5 \text{ m/s} $]]

b) Kuvaajalta voidaan löytää suurin nopeus 13,43 m/s kohdasta 8,04 s. Kuvaaja alla.

Kysytyssä yksikössä tämä on
[[$ 13,43 \text{ m/s}=13,43 \cdot 3,6 \text{ km/h}\approx 48 \text{ km/h} $]]
c) Kiihtyvyys on nopeuden kuvaajan derivaatta. Mittausohjelmistolla voidaan määrittää derivaatan eli tangentin kulmakertoimen arvoja eri kohdissa. Suurin arvo on noin 3,7 m/s2 kohdassa 3,2 s. Kuva alla.

d) Kuljettu matka on kuvaajan integraali eli kuvaajan ja x-akselin välinen pinta-ala. Mittausohjelmistolla saadaan määritettyä matkaksi
[[$ s=177,9 \text{ m}\approx 180\text{ m} $]]

e) Keskinopeus on siirtymä jaettuna ajalla. Siirtymä on yhtä suuri kuin matka, sillä liike etenee koko ajan samaan suuntaan. Koko mittauksen kesto on 21 s.
[[$ v_k=\dfrac{\Delta x}{\Delta t}=\dfrac{177,9\text{ m}}{21 \text{ s}}\approx 8,5 \text{ m/s} $]]
Esimerkki 3 malliratkaisu
a) Paikka on esitetty graafisesti ajan funktiona alla.
b) Putoamisliikettä voidaan mallintaa tasaisesti kiihtyvänä liikkeenä, jossa paikan yleinen lauseke on
[[$ x=x_0+v_0 t +\frac{1}{2}at^2 $]]
Lähdettäessä levosta kohdasta nolla lauseke on
[[$ x=\frac{1}{2}at^2 $]]
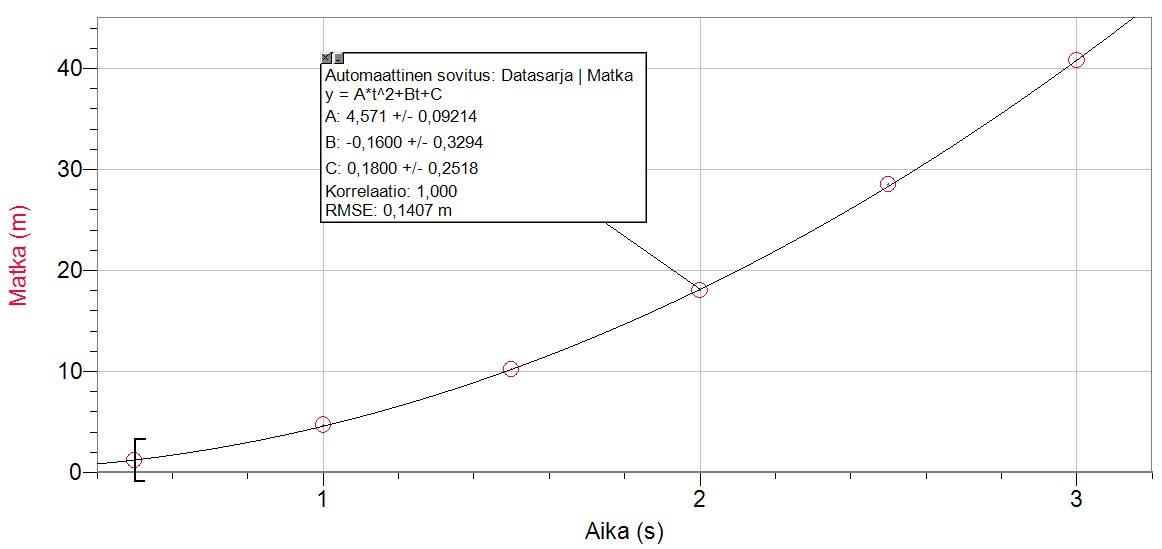
Paikan kuvaajaa voidaan siis mallintaa paraabelilla. Kun pistejoukkoon sovitetaan paraabeli, saadaan mittausohjelmistolla sen toisen asteen termin kertoimeksi 4,571 (m/s2) (Kuva alla). Paikan lausekkeessa tämä kerroin on puolet kiihtyvyydestä, eli
[[$ \frac{1}{2}a=4,571 \text { m/s}^2 $]].
Putoamiskiihtyvyys on siis mittauksen perusteella
[[$ a=2\cdot 4,571 \dfrac{\text{m}}{\text{s}^2}\approx 9,1 \dfrac{\text{m}}{\text{s}^2} $]]
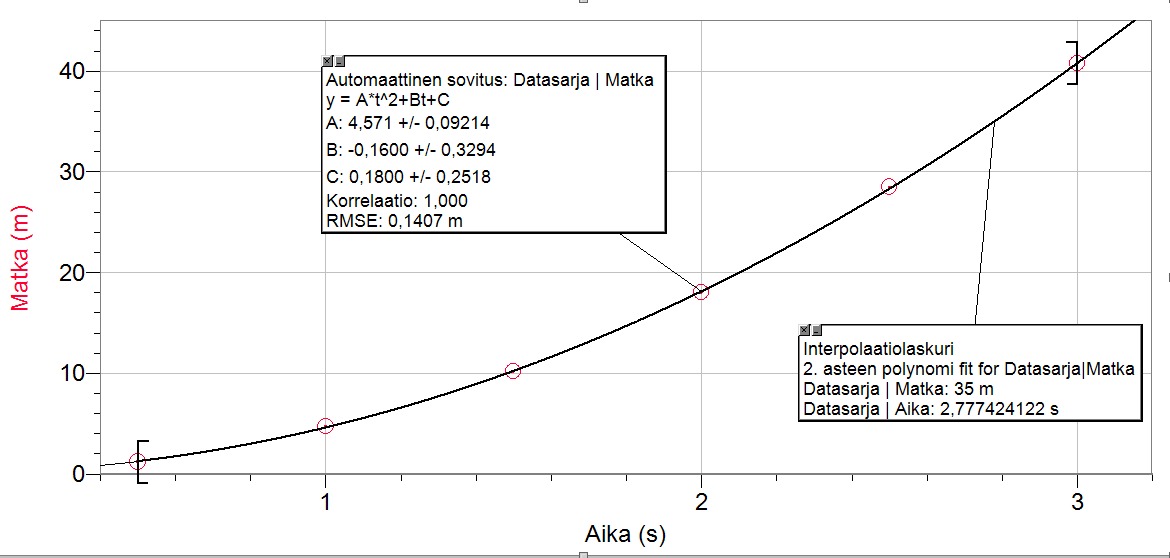
c) Mittausohjelmiston interpolointitoiminnolla voidaan määrittää ajanhetki, jolloin metka on 35 m. Alla olevan kuvaajan mukaan aika on noin 2,8 s.


b) Putoamisliikettä voidaan mallintaa tasaisesti kiihtyvänä liikkeenä, jossa paikan yleinen lauseke on
[[$ x=x_0+v_0 t +\frac{1}{2}at^2 $]]
Lähdettäessä levosta kohdasta nolla lauseke on
[[$ x=\frac{1}{2}at^2 $]]
Paikan kuvaajaa voidaan siis mallintaa paraabelilla. Kun pistejoukkoon sovitetaan paraabeli, saadaan mittausohjelmistolla sen toisen asteen termin kertoimeksi 4,571 (m/s2) (Kuva alla). Paikan lausekkeessa tämä kerroin on puolet kiihtyvyydestä, eli
[[$ \frac{1}{2}a=4,571 \text { m/s}^2 $]].
Putoamiskiihtyvyys on siis mittauksen perusteella
[[$ a=2\cdot 4,571 \dfrac{\text{m}}{\text{s}^2}\approx 9,1 \dfrac{\text{m}}{\text{s}^2} $]]

c) Mittausohjelmiston interpolointitoiminnolla voidaan määrittää ajanhetki, jolloin metka on 35 m. Alla olevan kuvaajan mukaan aika on noin 2,8 s.

Ratkaisu: esimerkki 4
Lasketaan tarvittavat ajanhetket piirtämistä varten.
Liike alkaa hetkellä 0 s.
Alkukiihdytys loppuu hetkellä 5,5 s.
Pyörä liikkuu tasaisesti 240 m nopeudella 7,5 m/s. Matkan lauseke on s = vt, joten voidaan ratkaista tasaisen liikkeen kesto t.
[[$ t=\frac{s}{v}=\mathrm{\frac{240\ m}{7{,}5\ \frac{m}{s}}\approx32\ s} $]]
Tasainen liike loppuu hetkellä 37,5 s.
Jarrutus kestää 3,8 s eli loppuu hetkellä 41,3 s.
Nopeuden kuvaaja on alla.
Kuvaajan asetuksista on otettu pistesymbolit pois ja valittu toiminto "yhdistä pisteet", jolloin saadaan halutunlainen kuvaaja.

Kokonaisuudessa kuljettu matka on nopeuden kuvaajan integraali eli sen rajaama pinta-ala x-akselin kanssa. Integraaliksi saadaan Loggerpro-ohjelmistolla 270 m. (kuva alla)

Liike alkaa hetkellä 0 s.
Alkukiihdytys loppuu hetkellä 5,5 s.
Pyörä liikkuu tasaisesti 240 m nopeudella 7,5 m/s. Matkan lauseke on s = vt, joten voidaan ratkaista tasaisen liikkeen kesto t.
[[$ t=\frac{s}{v}=\mathrm{\frac{240\ m}{7{,}5\ \frac{m}{s}}\approx32\ s} $]]
Tasainen liike loppuu hetkellä 37,5 s.
Jarrutus kestää 3,8 s eli loppuu hetkellä 41,3 s.
Nopeuden kuvaaja on alla.
Kuvaajan asetuksista on otettu pistesymbolit pois ja valittu toiminto "yhdistä pisteet", jolloin saadaan halutunlainen kuvaaja.

Kokonaisuudessa kuljettu matka on nopeuden kuvaajan integraali eli sen rajaama pinta-ala x-akselin kanssa. Integraaliksi saadaan Loggerpro-ohjelmistolla 270 m. (kuva alla)
