Edellisessä luvussa ratkottiin tilanteita joissa normaalijakauman keskiarvo ja keskihajonta oli annettuna. Silloin tehtävät ratkesivat Geogebran todennäköisyyskaskurilla helposti. Jos taas keskiarvoa tai keskihajontaa ei tunneta, voidaan tilanne ratkaista standardinormaalijakaumassa (eli normitetussa jakaumassa jossa keskiarvo on 0 ja keskihajonta 1) ja ratkaista keskiarvo tai keskihajonta normittamisyhtälöstä:

Esimerkki

Robotti täyttää kilon sokeripusseja. Sokeripussien paino noudattaa normaalijakaumaa keskiarvona robotille ilmoitettu keskiarvo ja keskihajontana 8.0 g. Kuinka suuri keskiarvo tulee asettaa, jotta 95 % sokeripusseista olisi painoltaan vähintään 1000 g?

Ratkaisu 

Keskiarvo [[$\mu$]] on tässä tuntematon. Tiedetään että [[$X \sim N(\mu, 8.0)$]]

Halutaan, että [[$P(1000 \leq X) = 0.95$]].
Jos Geogebran todennäköisyyslaskuriin syöttää tunnetut arvot, ei ohjelma osaa keskiarvoa tästä ratkoa, vaan menee säheltämiseksi. Siksi ratkotaan tilanne ensin standardijakaumassa.

Eli asetetaan todennäköisyyslaskurissa  [[$\mu=0, \sigma=1$]], oikeanpuoleinen jakaumapainike päälle ja todennäköisyydeksi 0.95.



Tästä nähdään, että normitettu z-arvo olisi -1.6449.


Normittaminen tapahtuu (katso edellinen luku 3.2) kaavalla
[[$z=\frac{x-\mu}{\sigma}$]].

Siispä ratkaistaan keskiarvo [[$\mu$]] yhtälöstä
[[$$-1.6449=\frac{1000-\mu}{8}$$]]

ja saadaan [[$$\mu \approx1013.1592.$$]]

Tämä täytyy nyt pyöristää ylöspäin koska halutaan vähintään 95 % todennäköisyys.
Eli keskiarvoksi on asetettava [[$$\mu=1014$$]].

Voimme tarkistaa tilanteen tietokoneen laskurilla:
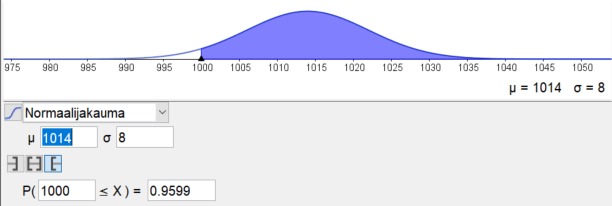Vastaus: Keskiarvoksi tulee asettaa 1014 grammaa.


Tehtäväsarja : 207, 209