Open Geogebra Geometry either as a desktop app, as a mobile app, or as a browser version. For ease of access, you may use the following link:

https://www.geogebra.org/geometry

1. Triangle angle sum theorem
   • Use the point and line segment tools to draw a triangle of any kind.
   • Name the vertices A, B, and C if they do not have these names automatically.
   • Use the parallel line tool to draw a line that is parallel to the side AB through vertex C.
   • Use the angle tool to mark the angles BAC (angle at vertex A), CBA (angle at vertex B), and ACB (angle at vertex C). Name the angles α, β, and γ, in the preceding order for A, B, and C.
   • Use the angle tool to mark the other angles at vertex A: one of them should be of identical size to β with AC as one of its sides, and one of them should be of identical size to α with BC as one of its sides.
     
     • Hint: You may have to add points to the parallel line using the point tool.
   • Add a text field using the text tool. Under additional settings, you will find a menu with the geogebra logo on it.
     • Choose α from this list.
     • Type the following symbol: +
     • Choose β from this list.
     • Type the following symbol: +
     • Choose γ from this list.
   • What did you accomplish and why?
2. Reflections with respect to a line
   • Right click on the white plane canvas.
     • Under coordinate grid options, select the largest squares.
   • Use the line tool to draw a line in any direction.
   • Use the polygon tool to draw a polygon of any kind.
   • Use the reflection tool to create a mirror image of the polygon with respect to the line.
   • Use the arrow tool to move your polygon.
     
     • If you move the polygon to the left, where does its mirror image move?
     • If you move the polygon two steps to the right and five steps upwards (you might remember this from Khan Academy as [[$(x+2,y+5)$]]), how many steps and in which direction does its mirror image move?
3. Reflections with respect to a point
   • Right click on the white plane canvas.
   • Under coordinate grid options, select the largest squares.
   • Use the point tool to draw a point.
   • Use the polygon tool to draw a polygon of any kind.
   • Use the reflection tool to create a mirror image of the polygon with respect to the point.
   • Use the arrow tool to move your polygon.
     
     • If you move the polygon to the left, where does its mirror image move?
     • If you move the polygon two steps to the right and five steps upwards (you might remember this from Khan Academy as [[$(x+2,y+5)$]]), how many steps and in which direction does its mirror image move?
4. Challenging task
   • Solve the challenging task using geogebra.
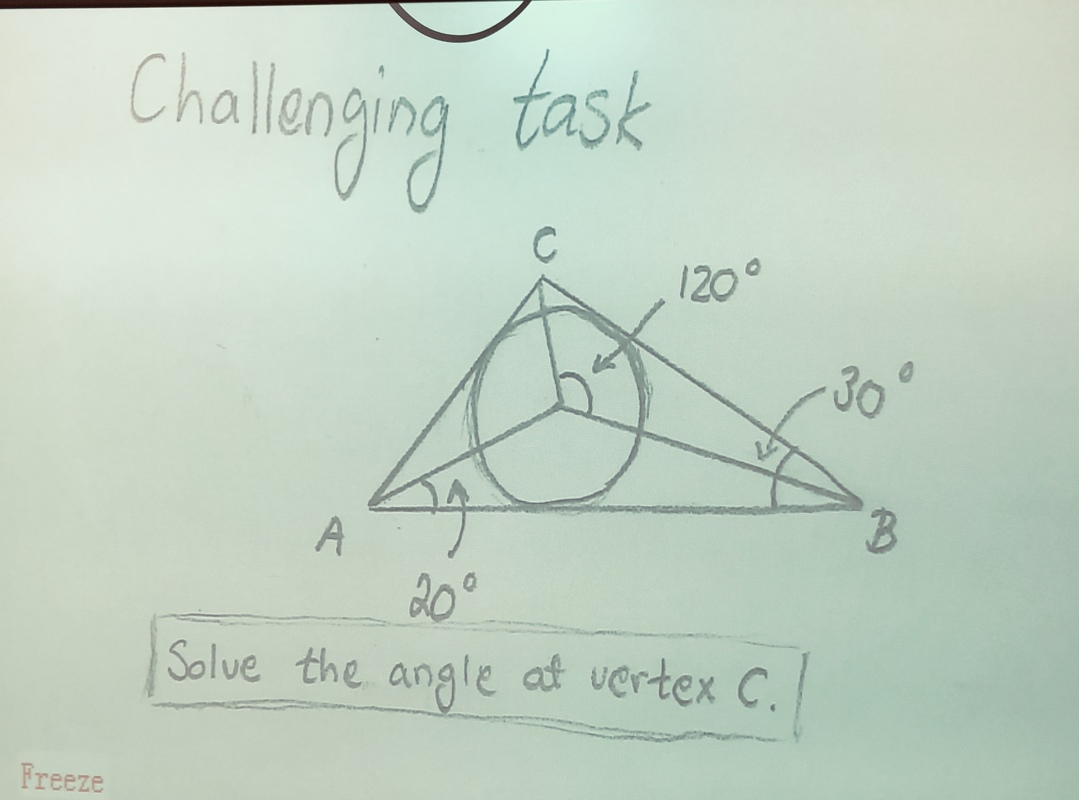
   • Remember to refer to chapter 2.12 Kolmion merkilliset pisteet​ for details on how to draw a circle within a triangle.