Epäyhtälöt koordinaatistossa
Tämä sivu oppikirjassa
Tämän sivun sisällöt liittyvät Sigma 6 -kirjassa kappaleeseen 1.3 Kahden muuttujan lineaarinen epäyhtälö.
Epäyhtälöistä
Yhtälöllä on selkeä ratkaisu.
Esimerkiksi
Yhtälön 2x + 1 = 9 toteuttaa vain muuttujan x arvo 4.
Yhtälön 2x2 + 1 = 9 toteuttaa vain kaksi muuttujan arvoa, jotka ovat +2 ja −2.
Epäyhtälön ratkaisuna saadaan alue, jolla on ääretön määrä arvoja.
Esimerkiksi
−2x + 6 < 8, joka voidaan ratkaista
−2x < 2
x > 1
Ratkaisusta nähdään, että mikä vain x:n arvo, joka on suurempi kuin 1 käy. Esimerkiksi 1,72 tai 14 tai 162 tai [[$ \sqrt{2} $]].
Voit kerrata (yhden muuttujan) ensimmäisen asteen epäyhtälön ratkaisua opetus.tv:n sivuilla.
Harjoituksia löydät esimerkiksi math.fi -sivustolta.
Yhden muuttujan epäyhtälöitä (eli sellaisia, joissa on vain x) on käsitelty aiemmalla kurssilla. Nyt perehdytään tarkemmin kahden muuttujan (x ja y) epäyhtälöihin.
Esimerkiksi
Yhtälön 2x + 1 = 9 toteuttaa vain muuttujan x arvo 4.
Yhtälön 2x2 + 1 = 9 toteuttaa vain kaksi muuttujan arvoa, jotka ovat +2 ja −2.
Epäyhtälön ratkaisuna saadaan alue, jolla on ääretön määrä arvoja.
Esimerkiksi
−2x + 6 < 8, joka voidaan ratkaista
−2x < 2
x > 1
Ratkaisusta nähdään, että mikä vain x:n arvo, joka on suurempi kuin 1 käy. Esimerkiksi 1,72 tai 14 tai 162 tai [[$ \sqrt{2} $]].
Voit kerrata (yhden muuttujan) ensimmäisen asteen epäyhtälön ratkaisua opetus.tv:n sivuilla.
Harjoituksia löydät esimerkiksi math.fi -sivustolta.
Yhden muuttujan epäyhtälöitä (eli sellaisia, joissa on vain x) on käsitelty aiemmalla kurssilla. Nyt perehdytään tarkemmin kahden muuttujan (x ja y) epäyhtälöihin.
Kahden muuttujan epäyhtälö
Kahden muuttujan yhtälöllä on ääretön määrä ratkaisuja.
Esimerkiksi
Suoran yhtälön y = 2x + 4 toteuttavat esimerkiksi pisteiden (0, 4), (1, 6) ja (1,7 ; 7,4) koordinaatit, mutta myös ääretön määrä muita.
Suoran yhtälön ratkaisut muodostavat koordinaatistossa suoran.
Yhtälön y = 2x2 toteuttavat esimerkiksi pisteiden (−2, 8), (−1, 2), (0,0), (1, 2) ja (2, 8) koordinaatit, mutta myös ääretön määrä muita.
Jos pisteet merkitään koordinaatistoon, muodostuu paraabeli.
Jos kyseessä on kuitenkin epäyhtälö, ratkaisua ei voi esittää koordinaatistossa viivana vaan ratkaisuna on jokin alue koordinaatistossa.
Harjoitus
Tutki täällä, miltä epäyhtälöiden ja yhtälöiden ratkaisut näyttävät koordinaatistossa.
Kahden muuttujan epäyhtälön ratkaisu esitetään usein piirroksena koordinaatistossa. Kyseessä on jokin alue koordinaatistossa, joten ensin pitää selvittää alueen raja. Sen jälkeen voidaan päätellä, kumpi puoli rajasta on oikea puoli ja esimerkiksi värittää oikea alue koordinaatistossa.
Esimerkiksi
Esitä epäyhtälön 6x − 2y < 4 ratkaisu koordinaatistossa.
Aloitetaan selvittämällä, mikä on alueen raja. Ratkaistaan ensin epäyhtälö y:n suhteen. (Muista pitää epäyhtälö epäyhtälönä.)
6x − 2y < 4 , josta siirretään x-termi oikealle
−2y < − 6x + 4 , josta jakamalla y:n kertoimella saadaan
y > 3x − 2
(huomaa, että epäyhtälön merkki kääntyi, koska jaettiin negatiivisella luvulla)
Alueen rajana toimii siis suora y = 3x − 2. Epäyhtälömuodosta nähdään, että ratkaisuna on alue, jossa y on suurempi kuin suora eli ratkaisuna on suoran yläpuolinen alue.
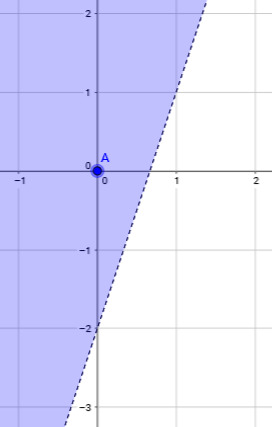
Tämä voidaan vielä varmistaa sijoittamalla alueella olevan pisteen koordinaatit alkuperäiseen epäyhtälöön. Esimerkiksi piste (0, 0) on selvästi halutulla alueella. Sijoitetaan sen koordinaatit alkuperäiseen epäyhtälöön.
6x − 2y < 4 ja piste (0, 0)
6 ∙ 0 − 2 ∙ 0 < 4
0 < 4, joka pitää paikkansa eli piste toteuttaa epäyhtälön. Vaikuttaa siltä, että ratkaisu on piirretty oikein.
Kuvassa raja on piirretty katkoviivalla, koska alkuperäinen epäyhtälö sisältää aidon epäyhtäsuuruuden ( < ). Viivalla olevat pisteet kuten esimerkiksi (0, −2) eivät toteuta epäyhtälöä.
Viivalla olevan pisteen koordinaateilla saadaan 6 ∙ 0 − 2 ∙ (−2) < 4 eli 4 < 4, mikä ei pidä paikkaansa.
Jos epäyhtälö sisältäisi yhtäsuuruuden ( < ), viivalla olevat pisteet olisivat osa ratkaisua.
Katso myös esimerkkivideo Sotungin matikka -kanavalta.
Harjoitus
Piirrä seuraavien epäyhtälöiden ratkaisut koordinaatistoon. Voit tarkastaa ratkaisut Geogebrassa.
a) y < 4x − 4
b) 2x + 4y > 8
c) 6 + 2y < 7x
Esimerkiksi
Suoran yhtälön y = 2x + 4 toteuttavat esimerkiksi pisteiden (0, 4), (1, 6) ja (1,7 ; 7,4) koordinaatit, mutta myös ääretön määrä muita.
Suoran yhtälön ratkaisut muodostavat koordinaatistossa suoran.
Yhtälön y = 2x2 toteuttavat esimerkiksi pisteiden (−2, 8), (−1, 2), (0,0), (1, 2) ja (2, 8) koordinaatit, mutta myös ääretön määrä muita.
Jos pisteet merkitään koordinaatistoon, muodostuu paraabeli.
Jos kyseessä on kuitenkin epäyhtälö, ratkaisua ei voi esittää koordinaatistossa viivana vaan ratkaisuna on jokin alue koordinaatistossa.
Harjoitus
Tutki täällä, miltä epäyhtälöiden ja yhtälöiden ratkaisut näyttävät koordinaatistossa.
Kahden muuttujan epäyhtälön ratkaisu esitetään usein piirroksena koordinaatistossa. Kyseessä on jokin alue koordinaatistossa, joten ensin pitää selvittää alueen raja. Sen jälkeen voidaan päätellä, kumpi puoli rajasta on oikea puoli ja esimerkiksi värittää oikea alue koordinaatistossa.
Esimerkiksi
Esitä epäyhtälön 6x − 2y < 4 ratkaisu koordinaatistossa.
Aloitetaan selvittämällä, mikä on alueen raja. Ratkaistaan ensin epäyhtälö y:n suhteen. (Muista pitää epäyhtälö epäyhtälönä.)
6x − 2y < 4 , josta siirretään x-termi oikealle
−2y < − 6x + 4 , josta jakamalla y:n kertoimella saadaan
y > 3x − 2
(huomaa, että epäyhtälön merkki kääntyi, koska jaettiin negatiivisella luvulla)
Alueen rajana toimii siis suora y = 3x − 2. Epäyhtälömuodosta nähdään, että ratkaisuna on alue, jossa y on suurempi kuin suora eli ratkaisuna on suoran yläpuolinen alue.

Tämä voidaan vielä varmistaa sijoittamalla alueella olevan pisteen koordinaatit alkuperäiseen epäyhtälöön. Esimerkiksi piste (0, 0) on selvästi halutulla alueella. Sijoitetaan sen koordinaatit alkuperäiseen epäyhtälöön.
6x − 2y < 4 ja piste (0, 0)
6 ∙ 0 − 2 ∙ 0 < 4
0 < 4, joka pitää paikkansa eli piste toteuttaa epäyhtälön. Vaikuttaa siltä, että ratkaisu on piirretty oikein.
Kuvassa raja on piirretty katkoviivalla, koska alkuperäinen epäyhtälö sisältää aidon epäyhtäsuuruuden ( < ). Viivalla olevat pisteet kuten esimerkiksi (0, −2) eivät toteuta epäyhtälöä.
Viivalla olevan pisteen koordinaateilla saadaan 6 ∙ 0 − 2 ∙ (−2) < 4 eli 4 < 4, mikä ei pidä paikkaansa.
Jos epäyhtälö sisältäisi yhtäsuuruuden ( < ), viivalla olevat pisteet olisivat osa ratkaisua.
Katso myös esimerkkivideo Sotungin matikka -kanavalta.
Harjoitus
Piirrä seuraavien epäyhtälöiden ratkaisut koordinaatistoon. Voit tarkastaa ratkaisut Geogebrassa.
a) y < 4x − 4
b) 2x + 4y > 8
c) 6 + 2y < 7x
Epäyhtälöryhmä
Aiemmin on jo tutkittu yhtälöpareja, joissa kahden ehdon piti täsmälleen toteutua. Ratkaisuja on silloin rajallinen määrä. Yhtälöparin ratkaisuna saadaan usein vain yksi piste.
Epäyhtälöt ovat tarpeen samankaltaisissa sovellustehtävissä. Epäyhtälöt kuvaavat ehtoja, jotka rajoittavat mahdollisia valintoja. Esimerkiksi jauhoja voidaan käyttää enintään niin paljon kuin niitä on varastossa tai voi olla, että pullia pitää myydä vähintään tietty määrä, jotta toiminnasta tulee voitollista. Epäyhtälöparin tai epäyhtälöryhmän ratkaisuna ei tule vain yksi piste. Pisteen sijaan saadaan alue, jolla on ääretön määrä pisteitä, jotka ovat kaikki hyväksyttäviä ratkaisuja.
Tutki epäyhtälöryhmän ratkaisua Geogebrassa ja vastaa sivulla oleviin kysymyksiin.
Tässä lyhyempi video epäyhtälöryhmän ratkaisusta. Tällä pitkähköllä videolla esitellään myös epäyhtälöryhmän ratkaisua.
Harjoitus
Tutki seuraavia epäyhtälöryhmiä koordinaatistossa.
- Ratkaise ensin epäyhtälö y:n suhteen.
- Merkitse epäyhtälö yhtälöksi ja piirrä rajaa kuvaava suora.
- Päättele kumpi puoli suorasta on voimassa.
Tai päättele suoraan, mistä koordinaatiston alueesta on kyse. Tarkasta piirroksesi Geogebrassa.
a)
[[$ \left\{\begin{matrix} y>0\\ x<0\\ \end{matrix}\right. $]]
b)
[[$ \left\{\begin{matrix} y>2\\ y<2x +2\\ \end{matrix}\right. $]]
c)
[[$ \left\{\begin{matrix} 2y-6x>-2\\ 8x<4y +16\\ \end{matrix}\right. $]]
d)
[[$ \left\{\begin{matrix} 4y>6x\\ 2x+y<7\\ y>-2 \\ x<6 \end{matrix}\right. $]]
Lisää harjoituksia löydät esimerkiksi vanhoista etälukiomateriaaleista täältä.
Sanallisen epäyhtälöryhmän ratkaiseminen lähtee liikkeelle muuttujien x ja y valitsemisesta. Yleensä tehtävässä tunnetaan monia asioita (esimerkiksi että jauhoja on saatavilla 6 kg tai että pullia pitää myydä vähintään 12 kpl). Tunnetut arvot eivät ole tuntemattomia. Tunnetut arvot auttavat muodostamaan rajoittavia ehtoja x:lle ja y:lle.
Esimerkiksi
Leipomossa valmistetaan kasvispiirakoita ja lihapiirakoita. Kasvispiirakkaan menee 100 g voita ja 200 g jauhoja. Lihapiirakkaan taas käytetään 200 g voita ja 300 g jauhoja. Voita on leipomon varastossa enää 6 kg ja jauhoja 12 kg. Esitä koordinaatistossa mahdollisten leivottavien piirakoiden määrät.
Tehtävä aloitetaan valitsemalla sopivat x ja y. Nyt tuntemattomia määriä ovat piirakoiden määrät, joten valitaan x = kasvispiirakoiden lukumäärä ja y = lihapiirakoiden lukumäärä.
Voin ja jauhojen määristä saadaan ehdot, jotka rajoittavat piirakoiden määriä. Muutetaan ensin kaikki massat kilogrammoiksi.
Kasvispiirakkaan menee 0,1 kg voita ja 0,2 kg jauhoja. Lihapiirakkaan menee 0,2 kg voita ja 0,3 kg jauhoja.
Jos leivotaan x kasvispiirakkaa, voita kuluu x ∙ 0,1 kg. Jos leivotaan y lihapiirakkaa, voita menee y ∙ 0,2 kg. Yhteensä kulutuksen pitää olla enintään 7 kg, joten saadaan epäyhtälö 0,1x + 0,2y < 7.
Jauhoista saadaan ehto 0,2x + 0,3y < 12.
Epäyhtälöryhmä on siis
[[$ \left\{\begin{matrix} 0,1x+0,2y\leq 7\\ 0,2x+0,3y\leq 12 \end{matrix}\right. $]]
, josta voidaan ratkaista
[[$ \left\{\begin{matrix} y\leq -0,5x+35\\ y\leq -\frac{2}{3} x+40 \end{matrix}\right. $]]
Lisäksi piirakoiden määrien täytyy olla ei-negatiiviset eli x > 0 ja y > 0.
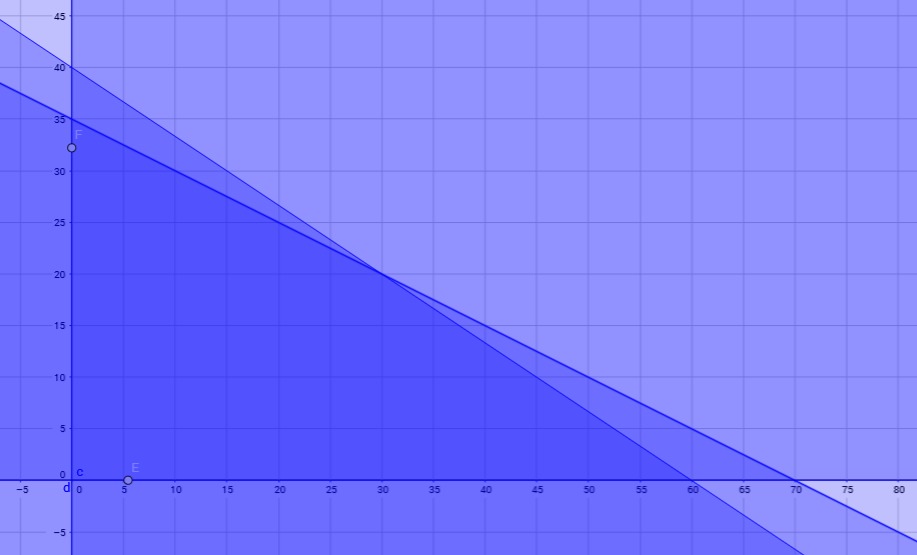
Kuvassa halutulla alueella ovat esimerkiksi pisteet (30, 20), (0, 35), (0, 0) ja esimerkiksi (10, 10).
Voitaisiin siis esimerkiksi tehdä 30 kasvispiirakkaa ja 20 lihapiirakkaa tai esimerkiksi vain 35 lihapiirakkaa. Toisaalta voitaisiin myös tehdä vaikka 10 kumpaakin piirakkaa, koska myös piste (10, 10) on sallitulla alueella.
Tällä pitkähköllä videolla käsitellään pari esimerkkiä sanallisista epäyhtälöryhmistä. Katso tehtävänanto, pysäytä video ja pohdi, osaisitko itse ratkaista tehtävän.
Tältä sivulta löydät tehtäviä, jotka yhdistelevät erilaisia tähän asti opittuja asioita.
Epäyhtälöt ovat tarpeen samankaltaisissa sovellustehtävissä. Epäyhtälöt kuvaavat ehtoja, jotka rajoittavat mahdollisia valintoja. Esimerkiksi jauhoja voidaan käyttää enintään niin paljon kuin niitä on varastossa tai voi olla, että pullia pitää myydä vähintään tietty määrä, jotta toiminnasta tulee voitollista. Epäyhtälöparin tai epäyhtälöryhmän ratkaisuna ei tule vain yksi piste. Pisteen sijaan saadaan alue, jolla on ääretön määrä pisteitä, jotka ovat kaikki hyväksyttäviä ratkaisuja.
Tutki epäyhtälöryhmän ratkaisua Geogebrassa ja vastaa sivulla oleviin kysymyksiin.
Tässä lyhyempi video epäyhtälöryhmän ratkaisusta. Tällä pitkähköllä videolla esitellään myös epäyhtälöryhmän ratkaisua.
Harjoitus
Tutki seuraavia epäyhtälöryhmiä koordinaatistossa.
- Ratkaise ensin epäyhtälö y:n suhteen.
- Merkitse epäyhtälö yhtälöksi ja piirrä rajaa kuvaava suora.
- Päättele kumpi puoli suorasta on voimassa.
Tai päättele suoraan, mistä koordinaatiston alueesta on kyse. Tarkasta piirroksesi Geogebrassa.
a)
[[$ \left\{\begin{matrix} y>0\\ x<0\\ \end{matrix}\right. $]]
b)
[[$ \left\{\begin{matrix} y>2\\ y<2x +2\\ \end{matrix}\right. $]]
c)
[[$ \left\{\begin{matrix} 2y-6x>-2\\ 8x<4y +16\\ \end{matrix}\right. $]]
d)
[[$ \left\{\begin{matrix} 4y>6x\\ 2x+y<7\\ y>-2 \\ x<6 \end{matrix}\right. $]]
Lisää harjoituksia löydät esimerkiksi vanhoista etälukiomateriaaleista täältä.
Sanallisen epäyhtälöryhmän ratkaiseminen lähtee liikkeelle muuttujien x ja y valitsemisesta. Yleensä tehtävässä tunnetaan monia asioita (esimerkiksi että jauhoja on saatavilla 6 kg tai että pullia pitää myydä vähintään 12 kpl). Tunnetut arvot eivät ole tuntemattomia. Tunnetut arvot auttavat muodostamaan rajoittavia ehtoja x:lle ja y:lle.
Esimerkiksi
Leipomossa valmistetaan kasvispiirakoita ja lihapiirakoita. Kasvispiirakkaan menee 100 g voita ja 200 g jauhoja. Lihapiirakkaan taas käytetään 200 g voita ja 300 g jauhoja. Voita on leipomon varastossa enää 6 kg ja jauhoja 12 kg. Esitä koordinaatistossa mahdollisten leivottavien piirakoiden määrät.
Tehtävä aloitetaan valitsemalla sopivat x ja y. Nyt tuntemattomia määriä ovat piirakoiden määrät, joten valitaan x = kasvispiirakoiden lukumäärä ja y = lihapiirakoiden lukumäärä.
Voin ja jauhojen määristä saadaan ehdot, jotka rajoittavat piirakoiden määriä. Muutetaan ensin kaikki massat kilogrammoiksi.
Kasvispiirakkaan menee 0,1 kg voita ja 0,2 kg jauhoja. Lihapiirakkaan menee 0,2 kg voita ja 0,3 kg jauhoja.
Jos leivotaan x kasvispiirakkaa, voita kuluu x ∙ 0,1 kg. Jos leivotaan y lihapiirakkaa, voita menee y ∙ 0,2 kg. Yhteensä kulutuksen pitää olla enintään 7 kg, joten saadaan epäyhtälö 0,1x + 0,2y < 7.
Jauhoista saadaan ehto 0,2x + 0,3y < 12.
Epäyhtälöryhmä on siis
[[$ \left\{\begin{matrix} 0,1x+0,2y\leq 7\\ 0,2x+0,3y\leq 12 \end{matrix}\right. $]]
, josta voidaan ratkaista
[[$ \left\{\begin{matrix} y\leq -0,5x+35\\ y\leq -\frac{2}{3} x+40 \end{matrix}\right. $]]
Lisäksi piirakoiden määrien täytyy olla ei-negatiiviset eli x > 0 ja y > 0.

Kuvassa halutulla alueella ovat esimerkiksi pisteet (30, 20), (0, 35), (0, 0) ja esimerkiksi (10, 10).
Voitaisiin siis esimerkiksi tehdä 30 kasvispiirakkaa ja 20 lihapiirakkaa tai esimerkiksi vain 35 lihapiirakkaa. Toisaalta voitaisiin myös tehdä vaikka 10 kumpaakin piirakkaa, koska myös piste (10, 10) on sallitulla alueella.
Tällä pitkähköllä videolla käsitellään pari esimerkkiä sanallisista epäyhtälöryhmistä. Katso tehtävänanto, pysäytä video ja pohdi, osaisitko itse ratkaista tehtävän.
Tältä sivulta löydät tehtäviä, jotka yhdistelevät erilaisia tähän asti opittuja asioita.