KPL 3 Lämpöenergia
Lämpöenergia on energialaji
Lämpöenergian säilymistä voidaan tarkastella yhdistämällä sama määrä erilämpöisiä vesiä yhteen. Astiassa on kylmää vettä, jonka lämpötila on 20 °C. Toisessa astiassa on yhtä paljon kuuman vettä, jonka lämpötila on 60 °C. Kun vedet yhdistetään samaan astiaan, saadaan vettä, jonka lämpötila on 40 °C. Molempien vesien lämpötilat muuttuvat yhtä paljon, koska veden määrä astioissa oli yhtä suuri. Energiaa siirtyy aina lämpimämmästä kohti kylmempää. Siten lämpimän veden lämpötila laski ja kylmän veden lämpötila nousi 20 astetta. Saavutettiin lämpötasapaino, jossa lämmin vesi oli luovuttanut energiaa saman verran kuin kylmä vesi oli ottanut vastaan.
Heti kun erilämpöiset vedet yhdistettiin samaan astiaan, alkoivat niissä olleiden lämpömittareiden lämpötilat tasaantumaan. Hetken kuluttua lämpömittarit näyttivät samaa lämpötilaa.
Ominaislämpökapasitetti
Millä videon materiaaleista (teräs, messinki kupari ja alumiini) on suurin ominaislämpökapasiteetti eli suurin kyky varastoida lämpöenergiaa? Miten voit havaita sen videon mittaustulosten perusteella?
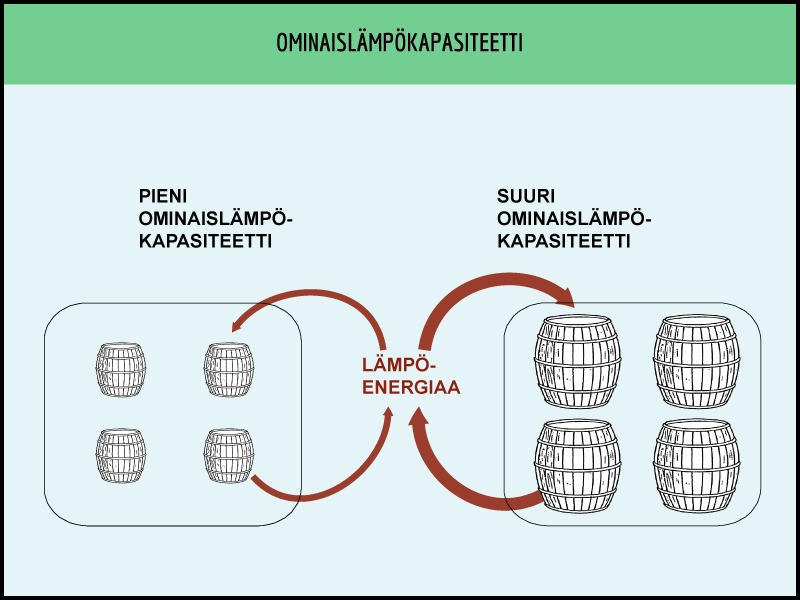
Ominaislämpökapasiteettia voidaan havainnollistaa kuvassa olevan mallin avulla. Vasemmanpuoleisen aineen ominaislämpökapasiteetti on pieni eli sen energian varastointikyky on pieni (säiliöt, joihin energia varastoituu, ovat pieniä). Kun säiliö täyttyy, on aineen lämpötila noussut yhden asteen. Oikeanpuoleisen aineen ominaislämpökapasiteetti on suuri (säiliöt ovat suuria). Mallilla voidaan selittää hyvin esimerkiksi metallien nopea lämpeneminen kuin myös jäähtyminen. Metalleilla säiliöt täyttyvät nopeasti eli aine lämpenee nopeasti, mutta ne myös tyhjenevät nopeasti eli aine viilenee nopeasti.
Aineen lämmittämiseen tarvittavan tai aineesta vapautuvan energian suuruus voidaan laskea, kun tiedetään aineen massa, lämpötilan muutos sekä aineen ominaislämpökapasiteetti.

[[$ \Delta $]] merkki luetaan ‘delta’. Fysiikassa sillä osoitetaan muutosta. Muutos lasketaan aina lopputilanne vähennettynä alkutilanteella. Esimerkiksi, jos lämpötila muuttuu 60 asteesta 150 asteeseen, on muutos 150 - 60 = 90 astetta.
Laskuesimerkkejä
Laske, kuinka paljon energiaa tarvitaan, kun 0,20 litraa 24 °C vettä lämmitetään 92 °C:een.
Ratkaisu: Kootaan tehtävän tiedot.
[[$ c = $]] 4,19 [[$ \dfrac{kJ}{kg\,°C} $]] (taulukoista katsottava tieto)
[[$ m = $]] 0,20 kg (1 litra vettä = 1 kg)
[[$ \Delta t = $]] 92°C - 24°C = 68°C
[[$ E = $]] ?
[[$ E = c \cdot m \cdot \Delta t = 4,19\, \dfrac{kJ}{kg\,°C} \cdot 0,20 \, kg \cdot 68\,°C = 56,984\,kJ \approx 57 kJ $]]
Vastaus: Energiaa tarvitaan 57 kJ.
Laskuesimerkki 2.
a) Laske, kuinka paljon energiaa tarvitaan, kun 5,0 kg 35 °C vettä lämmitetään kiehuvaksi.
b) Laske, kuinka monta astetta samalla energiamäärällä nousisi 5,0 kg massaisen rautakappaleen lämpötila.
Ratkaisu:
a) Kootaan tehtävän tiedot
[[$ m = $]] 5,0 kg
[[$ c = $]] 4,19 [[$ \dfrac{kJ}{kg\,°C} $]]
[[$ \Delta t = $]] 100 °C - 35 °C = 65 °C
[[$ E = $]] ?
[[$ E = c \cdot m \cdot \Delta t = 4,19 \, \dfrac{kJ}{kg\,°C} \cdot 5,0 \, kg \cdot 65 \, °C =1361,75 \, kJ \approx 1,4 \, MJ $]]
b) Kootaan tehtävän tiedot
[[$ E = $]] 1361,75 kJ
[[$ c = $]] 0,449 kJ/(kg°C)
[[$ m = $]] 5,0 kg
[[$ \Delta t = $]] ?
[[$ E = c \cdot m \cdot \Delta t $]] || : cm
[[$ \dfrac {E}{c \cdot m} $]] = [[$ \dfrac {c \cdot m \cdot \Delta t}{c \cdot m} $]](voidaan supistaa yhteiset tekijät pois)
[[$ \Delta t = \dfrac {E}{c \cdot m} $]]
[[$ \Delta t = \dfrac {1361,75\,kJ}{0,449\,\dfrac{kJ}{kg\,°C}·5,0\,kg} = 606,57\,°C ≈ 610\,°C $]]
Vastaus: Rautakappaleen lämpötila nousisi 610 astetta.