6.2 Tasavirtapiirit

Tasavirtapiirin toiminnan hahmotusta

Karkea mikroskooppinen malli virtapiirille

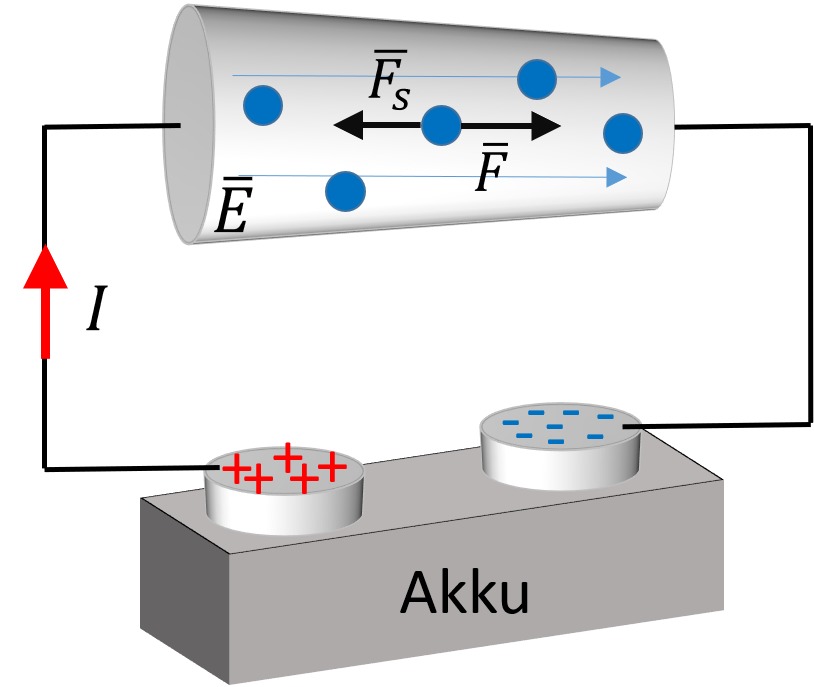Pariston kemialliset reaktiot tuottavat +/- varausta navoille. Varaus pyrkii purkautumaan eli napojen välillä on jännite.

Jännite synnyttää sähkökentän piirissä. Kenttä kohdistaa varauksiin (elektroneihin) sähköisen voiman F_s , joka alkaa liikuttaa niitä.

Materiaalissa liikkuviin elektroneihin kohdistuu väliaineen vastuksen kaltainen voima F, joka kumoaa sähköisen voiman ja liike on keskimäärin tasaista. Varauksen liike havaitaan sähkövirtana, joka synnyttää lämpöä sekä magneettisia ja kemiallisia vaikutuksia.

Sähkövirta on varauksen liikettä: [[$ I=\dfrac {\Delta Q}{\Delta t} $]]

Sähkövirran yksikkö ampeeri on varauksen yksikkö jaettuna ajan yksiköllä: [[$ 1\text{ A}=1\dfrac {\text{C}}{\text{s}} $]]

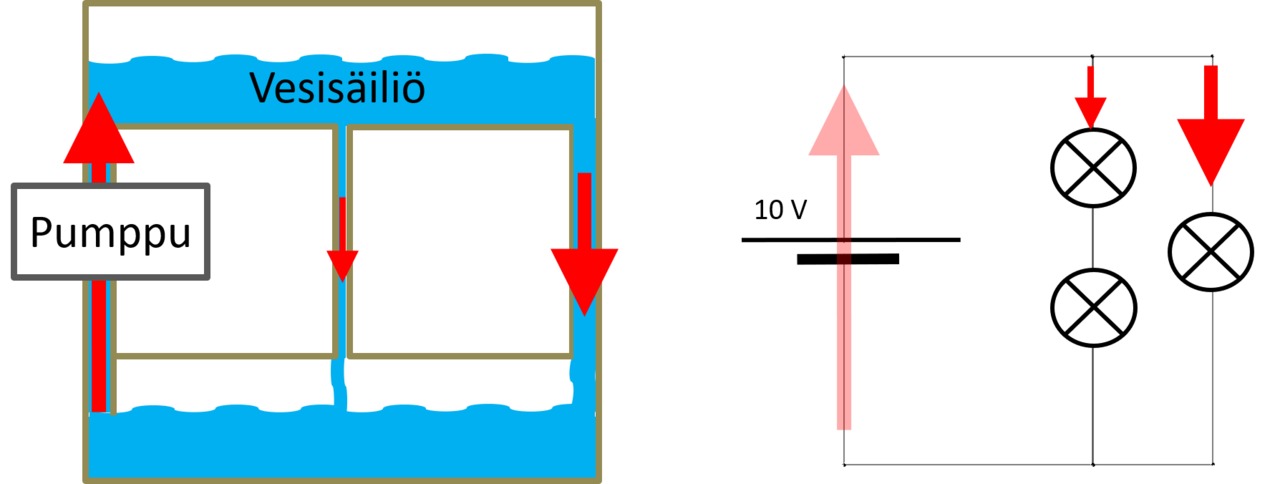
Veden virtauksen ja tasavirtapiirin analogia

Veden virtaus: Pumppu nostaa vettä ylös. Vesi virtaa potentiaalienergian vuoksi alaspäin. Virtausnopeus riippuu reitistä.

Sähkövirta: Paristo siirtää varausta korkeampaan potentiaaliin. Sähkövirta kulkee kohti matalampaa potentiaalia. Virran suuruus riippuu reitistä.

Kirchhoffin lait

Sähkövirta on varauksen liikettä ja sähkövaraus ei koskaan häviä. Näin ollen yhtenäisessä piirin osassa sähkövirta on sama joka kohdassa.

Virtapiirin haaroissa sähkövirta jakautuu osiin (ei välttämättä tasan), mutta kokonaissähkövirta säilyy.

Kirchhoffin I laki:
virtapiirin haaraan saapuvien sähkövirtojen summa on yhtä suuri kuin lähtevien sähkövirtojen summa

Pariston navoilla on pysyvä jännite eli potentiaaliero (kunnes paristo tyhjenee). Pariston sisältä siirtyy negatiiviselle navalle kemiallisissa reaktioissa vapautuvia elektroneja. Elektroneilla on tällöin potentiaalienergiaa, ja ne pyrkivät siirtymään paristoon kytketyn piirin kautta plusnavalle. (Sähkövirran suunnaksi on kuitenkin sovittu plusnavalta miinukselle.)

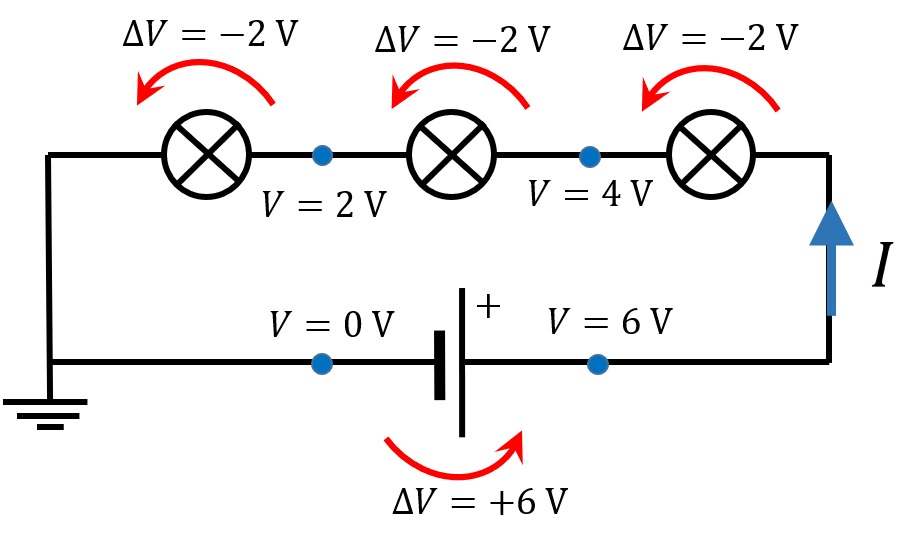Plusnavan potentiaali (V) on korkeampi kuin miinusnavan. Pariston sisällä sähkökentän potentiaali kasvaa mentäessä miinusnavalta plusnavalle. Sähkövirran suuntaan kuljettaessa potentiaali alenee piirin komponenteissa. Potentiaalin muutos eli kahden kohdan välinen jännite voidaan mitata jännitemittarilla. Piirin komponenteissa potentiaali alenee. Kun piiri on kierretty on pudottu takaisin miinusnavan potentiaaliin.

Jos kuljetaan suljettua virtapiiriä pitkin lähtien mistä tahansa pisteestä A niin, että palataan takaisin samaan pisteeseen, matkan varrella olevien potentiaalimuutosten täytyy olla yhteensä nolla. Tämä on Kirchhoffin II laki. Vastuksen läpi kuljettaessa potentiaali pienenee Ohmin lain mukaisen jännitteen [[$U=RI$]] verran.

Kirchhoffin II laki:
Suljetussa virtapiirissä potentiaalin muutosten summa on nolla:
[[$$ \Sigma \Delta V=0\\ $$]]
Jännitelähteiden napajännitteiden ja vastusten jännitteiden avulla ilmaistuna:
[[$$ U_1+U_2+...-R_1I-R_2I-...=0 $$]]

Kirchhoffin lait ovat virtapiirien peruslait. 1. laki ilmaisee varauksen säilymistä ja toista voidaan verrata esimerkiksi siihen, että "Suljetulla polkupyörälenkillä on yhtä paljon ylä- kuin alamäkiä". Lait voidaan hahmottaa myös edellä esitetyn veden virtausanalogian kautta.

Potentiaalin kuvaaja

Jännitteet piirin pariston ja komponenttien yli ovat potentiaalin muutoksia. Potentiaali ilmaisee sähköisen potentiaalienergian suuruutta (varattua hiukkasta kohden) kyseisessä kohdassa: U_AB = V_B- V_A

Potentiaalille sovitaan nollataso, yleensä maadoittamalla eli kytkemällä jokin kohta piiristä maahan.

Potentiaali eri kohdissa voidaan esittää paikan funktiona graafisesti. Tätä varten piiri ajatellaan suoristetuksi. Potentiaalin kuvaaja ilmentää eri kohtien välisiä jännitteitä sekä Kirchhoffin 2. lain toteutumista.

Ohmin laki ja vastusten kytkennät

Vastus on virtapiirien peruskomponentti. Vastuksen perusominaisuus on sen kyky vastustaa sähkövirran kulkua. Tätä kuvataan suureella resistanssi R, joka määräytyy Ohmin lain mukaan vastuksen jännitteen U ja sähkövirran I suhteena.

Ohmin laki: [[$R=\dfrac{U}{I} \qquad$]] [[$ \left( \text{resistanssi}=\dfrac{\text{jännite}}{\text{virta}} \right) $]]

Resistanssin yksikkö on ohmi Ω. Kaikilla komponenteilla on jonkinlainen resistanssi, mutta esim. kondensaattoreita käsitellään usein ideaalisina niin, että oletetaan niiden resistanssi nollaksi. Johtimen resistanssiin vaikuttavat sen materiaalin resistiivisyys, pituus ja poikkipinta-ala Ohmin toisen lain mukaisesti.

Joillakin komponenteilla jännitteen ja virran suhde ei ole vakio eivätkä ne siis noudata Ohmin lakia. Näin käyttäytyy esimerkiksi hehkulampun polttimo. Hehkulanka lämpenee huomattavasti sähkövirran kasvaessa ja tällöin kasvaa myös sen resistanssi. Kts. viereinen kuvaaja.

Resistanssi: komponentin tai konkreettisen, tietynmittaisen johtimen ominaisuus

Resistiivisyys: materiaalin ominaisuus

Johdelangan resistanssi: [[$R=\rho\dfrac{l}{A}\qquad\left(\text{resistanssi}=\text{resistiivisyys}\cdot\dfrac{\text{johtimen pituus}}{\text{johtimen poikkipinta-ala}}\right)$]]

Kytkettäessä vastuksia rinnan tai sarjaan saadaan yhdistelmä, jolla on myös vakioresistanssi. Systeemin kokonaisreistanssi voidaan laskea oheisilla säännöillä. Useiden vastusten kytkentä käyttäytyy niin kuin sen tilalla olisi yksi vastus jonka resistanssi on lasketun kokonaisresistanssin suuruinen.

Sarjaankytkettyjen vastusten kokonaisresistanssi:

[[$$R_{\text{KOK}}=R_1+R_2+R_3+\dots$$]] Rinnankytkettyjen vastusten kokonaisresistanssi: [[$$R_{\text{KOK}}=\left(\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\dots\right)^{-1}$$]]

Sisäinen resistanssi, lähdejännite ja paristojen kytkennät

Ideaalista paristosta saadaan aina sama jännite. Todellisilla paristoilla on aina resistanssia, minkä vuoksi paristosta saatava jännite vaihtelee. Todellista paristoa mallinnetaan niin, että sillä on vakiona pysyvä lähdejännite E sekä sisäinen resistanssi R_s. Lähdejännite voidaan mitata tavallisella jännitemittarilla kun paristoa ei ole kytketty mihinkään komponentteihin. Sisäisen resistanssin vuoksi pariston sisällä tapahtuu Ohmin lain mukainen jännitehäviö [[$ R_sI $]]. Kun tämä vähennetään pariston lähdejännitteestä saadaan ns. napajännite.

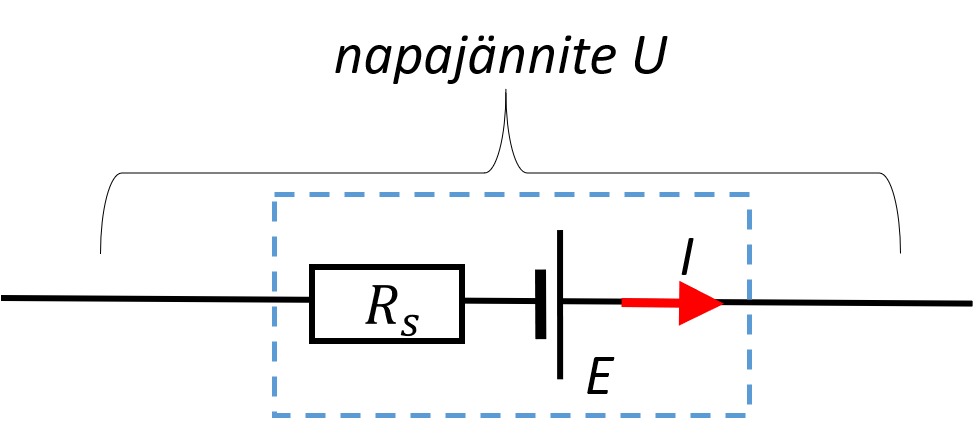Pariston napajännite on samalla ulkoiseen piiriin saatava jännite. Kirchhoffin toisen lain mukaisesti virtapiirissä pätee:

[[$ U=E-R_S I $]]

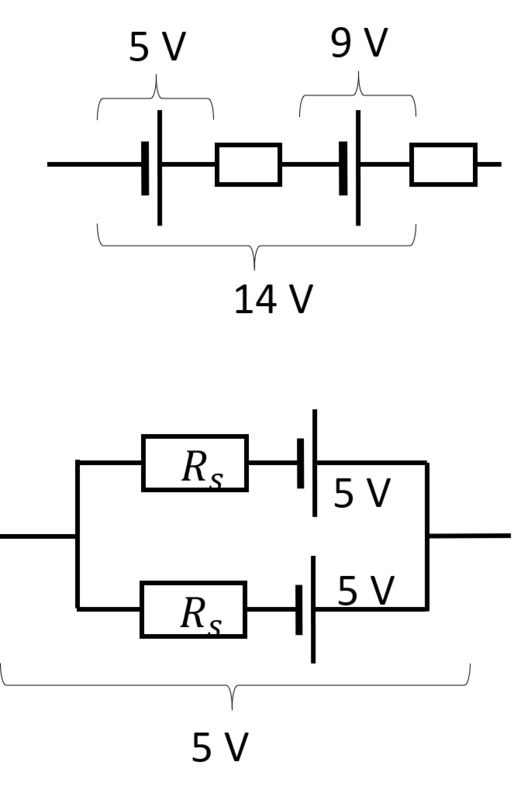
Paristoja voidaan kytkeä sarjaan tai rinnan. Sarjaankytkennässä paristojen lähdejännitteet summautuvat, mikäli ne on kytketty samansuuntaisesti. Myös sisäiset resistanssit summautuvat sarjaankytkennässä.

Kahden samanlaisen pariston rinnankytkentä ei kasvata kokonaislähdejännitettä. Sisäisten resistanssi pienenee kokonaisuudessaan, joten kytkennän napajännite on suurempi kuin yksittäisen pariston. Rinnankytkennän paristot myös kestävät pidempään, sillä molemmista paristoista saadaan sähkövirtaa.

Jos rinnankytkettyjen paristojen lähdejännitteet ovat eri suuret, voimakkaampi paristo pakottaa sähkövirtaa heikomman pariston lähdejännitteelle vastakkaiseen suuntaan. Tällöin pariston varaustaso heikkenee ja syntyy hukkalämpöä sisäisen resistanssin vuoksi.

Sähköteho

Jännitelähde tuottaa tehoa virtapiiriin. Teho kuluu piirin komponenteissa. Vastukset kuluttavat resistanssinsa vuoksi tehoa muuttaen pariston luovuttamaa energiaa lämmöksi.

Sähköteho

[[$ P=UI $]]

Joulen laki (vastuksen teho)

[[$ P=RI^2 $]]

Joissain tilanteissa on käytännöllistä laskea komponentin sähköteho sen napajännitettä ja resistanssia käyttäen:[[$ P=\dfrac{U^2}{R} $]]

Sovelmassa voit muuttaa pariston lähdejännitettä ja sisäistä resistanssia sekä paristoon kytketyn vastuksen resistanssia. Komponenttien tuottamat tai kuluttamat tehot määrittyvät näiden mukaisesti.