2.2 Monielektroniatomit
Energiatasot ja siirtymät monielektroniatomeissa
Vetyatomin ytimessä on yksi protoni ja ytimeen on sitoutunut yksi elektroni. Muiden atomien mallintaminen on monimutkaisempaa, koska niissä on useita keskenään vuorovaikuttavia elektroneja. Myös monielektroniatomien energiatilat ovat kvantittuneet, mikä ilmenee niiden viivamaisissa emissiospektreissä. Alla oleva kuva esittää neonin, heliumin ja vedyn spektriviivoja näkyvän valon alueella. Heliumilla ja neonilla on enemmän spektriviivoja, minkä selittää vetyä monimutkaisempi elektronitasorakenne.

Monielektroniatomeja mallinnetaan samoilla periaatteilla kuin vetyatomia, mutta niiden energiatiloille ei ole yksinkertaista laskukaavaa. Kaikki atomit absorboivat fotoneja, joiden energia [[$E_\text{fotoni}$]] on yhtä suuri kuin perustilan ja viritystilan välinen energiaero [[$\Delta E$]]. Atomit niin ikään emittoivat fotoneja, joiden energia on yhtä suuri kuin kahden tilan välinen energiaero. Energiaero ja fotonin aallonpituus kytkeytyvät siis toisiinsa seuraavalla kaavalla:
[[$ \quad \Delta E=\dfrac{hc}{\lambda_\text{fotoni}}$]]
Kuten aiemmin on kerrottu, elektronien käyttäytymistä atomissa kuvaa Schrödingerin yhtälö, josta voidaan ratkaista elektronien mahdolliset energiat. Monielektroniatomeille Schrödingerin yhtälö muodostuu monimutkaiseksi, eikä sitä pystytä ratkaisemaan tarkasti. Atomien perustilojen energiat ovat kuitenkin mitattavissa, ja muille tiloille voidaan ratkaista approksimaatiot. Tarkastelemalla aineen emissio- ja absorptiospektrejä voidaan laskea siirtymien energiat ja siten päätellä mahdolliset energiatilat. Niitä voidaan sitten vertailla erilaisiin Schrödingerin yhtälön approksimaatioihin. Mahdolliset energiatilat on kirjattu taulukoihin. Monipuolinen ja ilmainen lähde on esimerkiksi NIST (National Institute of Standards and Technology).
![]() Taulukoita alkuaineiden ominaisuuksista, mm. energiatilat (NIST eng.)
Taulukoita alkuaineiden ominaisuuksista, mm. energiatilat (NIST eng.)
Atomin monimutkaistuessa energiatilojen lukumäärä lisääntyy. Vaihtoehtoisia siirtymiä tilalta toiselle on enemmän ja spektriviivoja nähdään useampia kuin vedyllä. Alla on osa heliumin emissiospektriä.
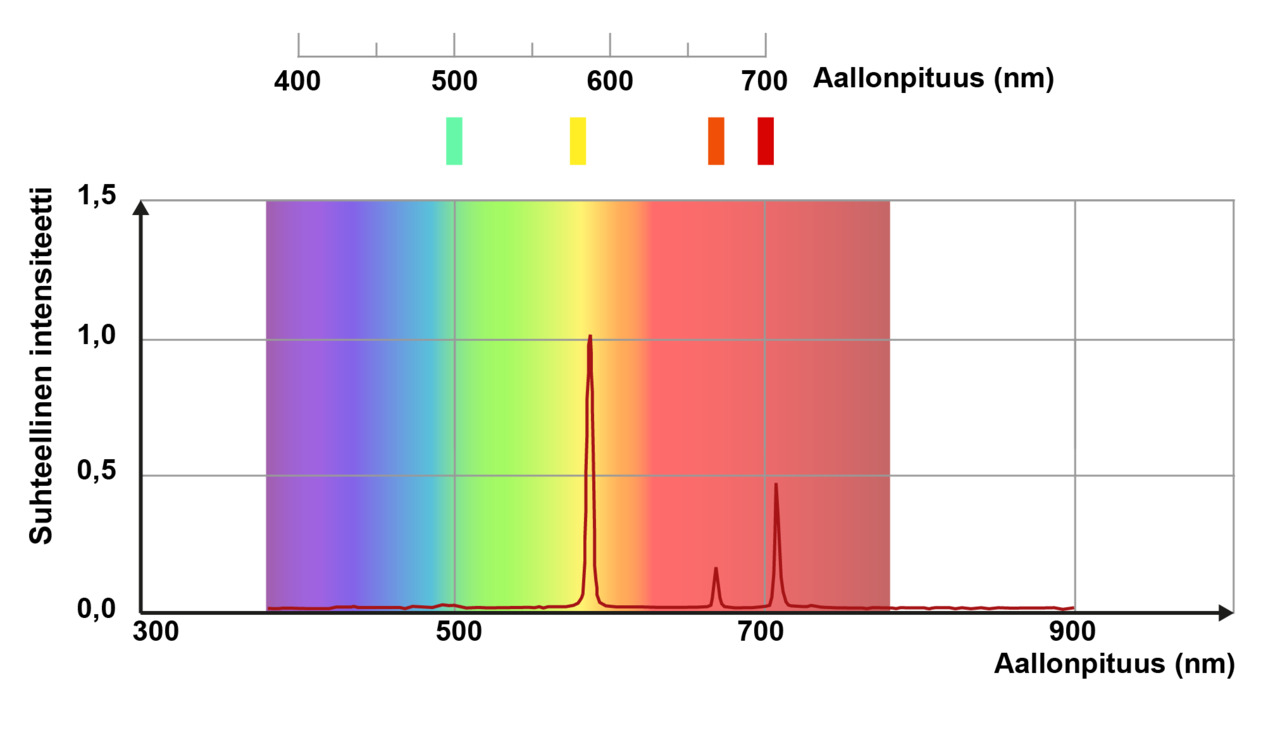
Heliumin emissiospektrin kirkkaimman kellertävän viivan aallonpituus on noin 590 nm. Tämän perusteella tiedetään, että spektriviivan synnyttäneiden energiatilojen välinen energiaero on ollut
[[$ \quad \Delta E=E_\text{fotoni} \\
\quad E_{\text{fotoni}}=\dfrac{hc}{\lambda} \\
\quad E_{\text{fotoni}}=\dfrac{4{,}136\cdot 10^{-15} \textrm{ eVs}\cdot 2{,}998\cdot 10^8 \textrm{ m/s}}{590 \cdot 10^{-9} \textrm{ m}}\approx 2{,}1 \textrm{ eV} $]]
Ohessa on heliumin energiatasokaavio, jossa on joitakin heliumin tunnettuja energiatiloja. Keltaista valoa vastannut energia 2,1 eV on siirtymä kolmannelta viritystilalta ensimmäiselle viritystilalle. Siirtymä on merkitty kuvaan. Heliumin perustilan ja viritystilojen välillä on suuri, yli 20 eV:n, energiaero. Näin ollen heliumin siirtyessä perustilaan emittoituu UV-säteilyä. Näkyvää valoa syntyy vain viritystilojen välisissä siirtymissä.

Elektronin kvanttitilat atomissa
Jokaista mahdollista elektronin energiatilaa vastaa tietty elektronin sijainnin todennäköisyysjakauma. Kuten energiatilat, myös todennäköisyysjakaumien muodot saadaan ratkaistua Schrödingerin yhtälöstä. Vetyatomille ratkaisut ovat tarkkoja ja monielektroniatomeille yleensä approksimaatioita. Alueita, joissa elektroni jakauman perusteella todennäköisimmin on, kutsutaan orbitaaleiksi. Kuten energiatiloja, myös orbitaaleja on vain muutama mahdollinen. Kvanttiluvuilla voidaan kuvata, millä orbitaalilla elektroni on. Elektronin tila määräytyy neljän kvanttiluvun kautta.
Pääkvanttiluku [[$n$]] kuvaa, kuinka kaukana atomiytimestä elektroni keskimäärin sijaitsee. Mitä suurempi pääkvanttiluku on, sitä kauemmas todennäköisyysjakauma on keskittynyt. Pääkvanttiluku voi saada arvokseen mitä tahansa positiivisia kokonaislukuja (1, 2, 3, ...). Arvoille käytetään joskus myös tunnuksia K, L, M, N, ... ja pääkvanttiluvusta usein myös nimitystä päätaso.
Vetyatomin tapauksessa pelkkä pääkvanttiluku määrää elektronin energiatilan lähes täsmälleen. Energiatasokaavassa
[[$\qquad E_n=-\dfrac{1}{n^2}\dfrac{m_\text{e}e^4}{8\epsilon_0^2h^2}$]]
ei ole muita kvanttilukuja kuin pääkvanttiluku [[$n$]]. Tästä johtuen vedyn energiatasokaavio ja emissiospektri ovat hyvin yksinkertaiset. Tarkoissa mittauksissa on havaittu muista kvanttiluvuista johtuvia hyvin pieniä korjauksia energiatasoihin.
Sivukvanttiluku [[$\ell$]] kertoo orbitaalin muodon. Kuvissa atomiydin on keskellä. Atomiytimen ympärille piirretään alue, jonka sisällä elektroni on 95 %:n todennäköisyydellä. Sivukvanttiluku voi saada arvokseen kokonaisluvun välillä [[$0\le \ell \le n-1$]]. Sivukvanttiluvun arvoille käytetään myös tunnuksia s, p, d, f, ...
Kun ollaan päätasolla 1 eli pääkvanttiluku on 1, sivukvanttiluvulle on vain 1 mahdollinen arvo, 0 eli s. Esimerkiksi päätasolla 3 sivukvanttiluvulle on kolme mahdollista arvoa, 0, 1 ja 2 eli s, p ja d. Nämä edustavat eri muotoisia orbitaaleja. Vetyatomilla orbitaalin muoto ei vaikuta energiaan. Monielektroniatomeilla elektronit eivät vuorovaikuta pelkästään ytimen kanssa vaan myös keskenään. Siksi orbitaalin muodolla eli sivukvanttiluvulla on merkitystä energiatasolle. Monielektroniatomien energiatasokaaviot ovat yleensä huomattavasti monimutkaisempia kuin vedyllä, ja niillä on enemmän mahdollisia energiatasoja. Kuten aiemmin on todettu, monielektroniatomien energiatasoille ei ole yleistä kaavaa, vaan ne määritetään kokeellisesti viivaspektrien perusteella.

Magneettinen kvanttiluku [[$m$]] kertoo orbitaalin asennon. Esimerkiksi p-orbitaaleja on kolme, koska yllä näkyvät p-orbitaalin pallukat voivat olla x-, y- tai z-suunnassa. Eri asentojen vaikutus kvanttitilan energiaan havaitaan atomin ollessa ulkoisessa magneettikentässä. Siksi asentoa kuvaavaa kvanttilukua kutsutaan magneettiseksi kvanttiluvuksi. Magneettikentän vaikutus energiatasoihin paljastuu siten, että aineen emissiospektrin spektriviivat jakaantuvat magneettikentässä useampiin lähekkäisiin spektriviivoihin. Magneettinen kvanttiluku voi saada kokonaislukuarvoja välillä [[$-\ell \dots \ell$]], eli vaihtoehtoisia asentoja on sitä enemmän, mitä monimutkaisemmasta muodosta on kyse.
Spinkvanttiluku [[$m_s$]] erottaa kaksi muuten samassa tilassa olevaa elektronia toisistaan. Spinkvanttiluku vaikuttaa elektronin käyttäytymiseen vastaavalla tavalla kuin makroskooppisen hiukkasen käyttäytymiseen vaikuttaa sen pyörimissuunta itsensä ympäri, ts. pyöriikö hiukkanen myötä- vai vastapäivään. Spinkvanttiluvulla on kaksi arvoa, jotka merkitään +½ ja -½. Elektronin spiniä ei kuitenkaan pidä mieltää elektronin pyörimisliikkeeksi.
Elektronien asettuminen kvanttitiloille
Wolfgang Paulin (1900–1958) mukaan nimetyn Paulin kieltosäännön mukaisesti täsmälleen samalla kvanttitilalla voi olla vain yksi elektroni. Siten kahdella elektronilla vähintään yhden kvanttiluvuista [[$n, \ell, m, m_s$]] täytyy erota toisistaan.
Monielektroniatomissa elektronit asettuvat kvanttitiloille siten, että matalaenergisimmät tilat täyttyvät ensin. Jokaista pääkvanttiluvun määräämää energiatasoa vastaa tietty määrä sivukvanttiluvun mukaisia alatasoja. Ensimmäisen pääkvanttiluvun arvo on 1. Koska sivukvanttiluku on aina pienempi kuin pääkvanttiluku, sen ainoa mahdollinen arvo on tällä päätasolla 0. Myös magneettinen kvanttiluku saa tällöin arvon 0. Spinkvanttiluku voi saada kaksi arvoa (+1/2 tai -1/2), joten tasolle [[$n=1$]] mahtuu kaksi elektronia.
Pääkvanttiluvun kasvaessa muilla kvanttiluvuilla on useampia mahdollisia arvoja. Alla oleva kaavio kuvaa tilojen rakentumista tasolle [[$n=2$]] saakka. Huomataan, että yhdistelmiä on kahdeksan. Päätasolle 2 mahtuu kahdeksan elektronia.

Vety ja helium perustilalla
Vedyn ainoa elektroni on perustilalla päätasolla [[$n=1$]]. Tälle energiatasolle mahtuu kaksi elektronia spinkvanttiluvun erottamina. Heliumatomilla on kaksi elektronia, joten molemmat elektronit mahtuvat tasolle [[$n=1$]].
Litium ja beryllium perustilalla
Litiumilla on kolme elektronia, joten kolmas elektroni ei enää mahdu päätasolle [[$n=1$]]. Litiumin perustilalla kolmas elektroni sijoittuu tasolle [[$n=2$]], jossa elektroni sijoittuu matalimmalle alatasolle [[$\ell=0$]]. Tälle alatasolle mahtuu kaksi spinkvanttiluvun erottamaa elektronia. Berylliumilla on neljä elektronia, joten atomissa täyttyy pääkvanttiluvun [[$n=2$]] alataso [[$\ell =0$]].
Muut 2. jakson alkuaineet
Energiatasolla [[$n=2$]] sivukvanttiluku voi saada nollan lisäksi arvon [[$\ell = 1$]]. Tällä alatasolla magneettinen kvanttiluku [[$m$]] voi saada arvot -1, 0, 1. Koska jokaiselle tasolle mahtuu kaksi elektronia spinkvanttiluvun erottamina, on täydellä alatasolla [[$\ell = 1$]] kuusi elektronia ja tasolla [[$n=2$]] yhteensä kahdeksan elektronia. Kun tähän lasketaan tilalla [[$n=1$]] olevat kaksi elektronia, voi atomilla tilalla [[$n=2$]] olla enintään kymmenen elektronia. Täysien kuorien atomit ovat jalokaasuja, ja edellä mainittu kymmenen elektronin atomi on neon. Alkuaineilla litiumista neoniin täytetään tilaa [[$n=2$]]. Nämä ovat 2. jakson alkuaineita.
Atomien ionisaatioenergiat ja jaksollinen järjestelmä
Jos atomin pääkvanttiluvun määräämä elektronikuori on täysi, atomin ei ole energeettisesti edullista ottaa vastaan tai luovuttaa elektronia. Tällaiset atomit vuorovaikuttavat heikosti toisten atomien kanssa. Niiden ionisoimiseen tarvitaan paljon energiaa, ja ne kuuluvat jalokaasuihin. Vetyatomilla ionisaatioenergia on 13,6 eV. Heliumilla se on suurempi: 24,6 eV. Heliumin ionisaatioenergia on atomeista suurin, koska elektronikuori on täysi ja elektronit sijaitsevat lisäksi lähellä atomiydintä.
Litiumilla ionisaatioenergia on selvästi vetyä alhaisempi: 5,4 eV. Tämä johtuu siitä, että energiataso [[$n=1$]] on täysi ja kolmas elektroni sijoittuu energiatasolle [[$n=2$]], kauemmaksi ytimestä. Sisemmän energiatason elektronit varjostavat uloimman elektronin ja ytimen välistä vuorovaikutusta pienentäen ionisaatioenergiaa. Kun uloimmalla energiatasolla on vain yksi elektroni, atomi vuorovaikuttaa herkästi muiden atomien tai ionien kanssa. Tällaisten alkuaineiden ionisaatioenergia on alhainen, ja ne luopuvat uloimmasta elektronistaan helposti.
Ionisaatioenergia kasvaa pääsääntöisesti saman energiatason elektronien lukumäärän lisääntyessä. Joitain poikkeuksia tosin on. Esimerkiksi berylliumin (neljä elektronia) ionisaatioenergia on suurempi kuin boorin (viisi elektronia). Berylliumilla on täysi pääkvanttiluvun, [[$n=2$]], alataso, [[$\ell=0$]]. Boorilla yksi elektroni sijoittuu alatasolle [[$\ell=1$]], jolloin se on helpommin irrotettavissa atomista. Suurimmat ionisaatioenergiat havaitaan jalokaasuilla, joilla on täydet uloimman päätason alatasot. Alla on kaavio, jossa on kuvattu ionisaatioenergia atomin järjestysluvun mukaan.

| Alkuaine | Elektronirakenne | Ionisaatioenergia (eV) |
|---|---|---|
| Vety | 1s1 | 13,6 |
| Helium | 1s2 | 24,6 |
| Litium | 1s22s1 | 5,4 |
| Beryllium | 1s22s2 | 9,3 |
| Boori | 1s22s22p1 | 8,3 |
| Hiili | 1s22s22p2 | 11,3 |
| Typpi | 1s22s22p3 | 14,5 |
| Happi | 1s22s22p4 | 13,6 |
| Fluori | 1s22s22p5 | 17,4 |
| Neon | 1s22s22p6 | 21,6 |
| Natrium | 1s22s22p63s1 | 5,1 |
Yllä olevassa taulukossa elektronirakenne on ilmaistu käyttämällä sivukvanttiluvulle [[$\ell$]] arvoja s, p, d, f, ... lukuarvojen 0, 1, 2, 3, ... sijaan. Esimerkiksi typen rakenteen merkintä 1s22s22p3 tarkoittaa, että tilalla [[$n=1$]], [[$\ell=0$]] on kaksi elektronia (eri spinkvanttiluvuilla), tilalla [[$n=2$]], [[$\ell=0$]] on myös kaksi elektronia (taas eri spinkvanttiluvuilla), ja tilalla [[$n=2$]], [[$\ell=1$]] on kolme elektronia (eri magneettikvanttiluvuilla, ts. eri asennossa olevilla orbitaaleilla).
Kolmatta jaksoa raskaammat alkuaineet
Energiatason [[$n=3$]] jalokaasu on argon. Argonilla on 18 elektronia. Seuraavalla alkuaineella kaliumilla 19. elektroni sijoittuu uudelle energiatasolle [[$n=4$]], vaikka energiatasolla [[$n=3$]] on alataso 3d täyttämättä. Alatason 3d energia on kuitenkin suurempi kuin tilan 4s. Näin ollen kalium aloittaa neljännen jakson. Vasta kun alataso 4s on täysi, taso 3d alkaa täyttyä.

Kvanttimekaniikan ymmärtäminen on selittänyt jaksollisen järjestelmän rakentumisen edellä kuvatulla tavalla. Jaksollinen järjestelmä muotoutuu sen mukaisesti, miten elektronit täyttävät energiatiloja.

Pysähdy pohtimaan
Esimerkkejä
Esimerkki 1
Oheiseen heliumin energiatasokaavioon on merkitty eräs mahdollinen siirtymä viritystilalta toiselle. Näkyykö kyseisen säteilyn piikki oheisessa spektrissä?
Esimerkki 2
Tarkastellaan perustilalla olevan neonkaasun ionisaatiota. Neonatomin ionisaatioenergia on 21,56 eV.- Kuinka suuri elektronin nopeuden on oltava, jotta se pystyisi liike-energiansa ansiosta ionisoimaan neonkaasun atomin?
- Mikä on sellaisen fotonin aallonpituus, joka voi ionisoida neonkaasun atomin?
