The faces of a polyhedron consist of polygons. The interfaces of a regular polyhedron can also be shaped like different regular polygons. In Archimedean solids, the upper and lower surfaces are regular polygons, whereas the sides consist of squares. If simple facets are left out of the calculations, there are [[$ 13 $]] different kinds of Archimedean solids.

There are only five Platonic solids. The best known of these is a square cube, or hexahedron. Platonic solids consisting of triangles are the tetrahedron (4-faceted), the octahedron (8-faceted), and the icosahedron (20-faceted).

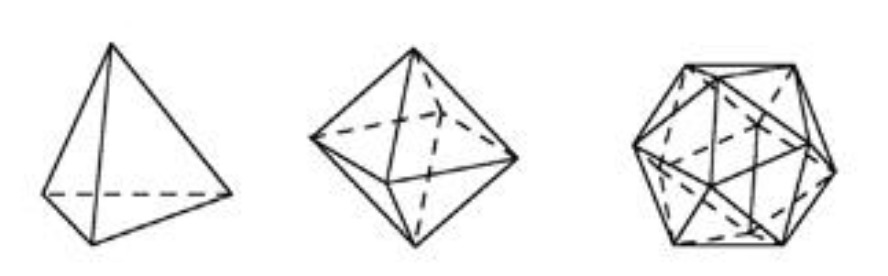
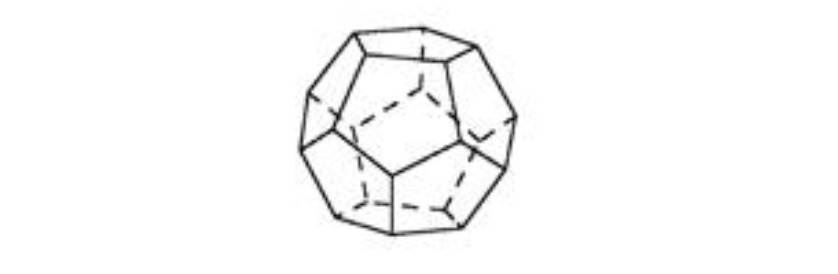
The dodecahedron (12-sided) consists of pentagons.

If the edge of a regular polyhedron is [[$ a $]], the areas and volumes of the pieces can be calculated using the formulas displayed in the table below.

	Tetrahedron	Hexahedron	Octahedron	Dodecahedron	Icosahedron
area	[[$ a^2\sqrt3 $]]​	[[$ 6a^2 $]]​	​ [[$ 2a^2\sqrt3 $]]​	[[$ 3a^2\sqrt{5(5 + 2\sqrt5)} $]]​	[[$ 5a^2\sqrt3 $]]​
volume	[[$ \displaystyle\frac{a^3\sqrt2} {12} $]]​	[[$ a^3 $]]​	[[$ \displaystyle\frac{a^3\sqrt2} {3} $]]​	[[$ \displaystyle\frac {a^3(15+7\sqrt{5})} {4} $]]​	[[$ \displaystyle\frac{5a^3(3+\sqrt5)} {12} $]]​

Example 1

A spice mixture is packaged in a tetrahedral container with an edge length of [[$ 3,8 \;\text {cm} $]]​. Calculate the package's

a) area.

​[[$ A = a^2 \sqrt {3} = (3,8 \;\text {cm}^2 \sqrt {3} ≈ 25 \;\text {cm}^2 $]]​

b) volume.

​[[$ V = \displaystyle\frac{a^3\sqrt2} {12} = \displaystyle\frac{(3,8 \;\text {cm})^3\sqrt2} {12} ≈ 6,5 \;\text {cm}^3 $]]​

Answer: The surface area of the package is [[$ 25 \;\text {cm}^2 $]]​. The volume of the package is [[$ 6,5 \;\text {cm}^3$]]​.